贝叶斯优化 Bayesian Optimization

一、介绍

  在机器学习的许多模型中，包括决策树、支持向量机、神经网络，都存在着大量的超参数需要凭经验设定（学习率、决策树深度、神经元个数等），也可以使用grid search或者random search的方法进行自动设置。本文介绍另外一种自动化调参的方法贝叶斯优化（Bayesian Optimization,BO）。

二、问题描述

  优化问题的数学形式可以表示为:
$$x^{\ast }=\underset{x}{\mathrm{argmax}}f(x)$$

  BO其实是一种优化方法，适用于大部分优化问题，这些问题往往具备以下的几个特点：

• 优化问题$f$是一个黑盒(black box)问题，不能得到其解析解
• 优化问题$f$的一次评估是昂贵的(耗时，耗money)
• 该问题的观测值可能存在噪声

三、算法细节

   贝叶斯优化主要由两部分组成，第一个部分是概率代理模型，它由一个先验分布和一个观察模型组成，前者捕捉我们对未知目标函数行为的信念，后者描述数据生成机制。常用的模型有高斯过程模型和随机森林。这类模型有一个特点：既可以对新的输入产生预测的输出也可以产生预测值的不确定性。第二个部分是采集函数(Acquisition function) 用于产生新的$x$.贝叶斯模型的算法框架如下所示。

首先可以随机抽样一部分点得到$D=(x_1,y_1),\cdots ,(x_m,y_m)$用于构建代理模型，然后通过最大化采集函数$\alpha$得到下一个点$x_{n+1}$,通过真实的评价函数$f(x_{n+1})$得到观测值$(x_{n+1},y_{n+1})$,将其添加进$D$中并调整代理模型，进入下一次迭代。

  下面分别介绍代理模型部分和采集函数。

3.1 概率代理模型

  比较常见的代理模型是高斯过程(GP),具体的介绍可以看这篇笔记：高斯过程
最终的高斯过程可以得到：

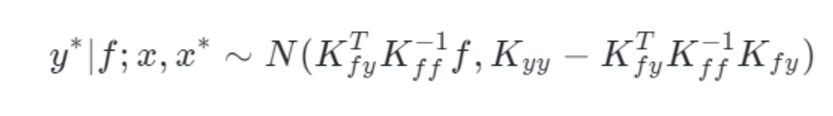
即：

μ = K f y T K f f − 1 f , c o v = K y y − K f y T K f f − 1 K f y \mu = K_{fy}^TK_{ff}^{-1}f,\\ c