C语言实现笛卡尔树

先来回顾一下笛卡尔树的性质：笛卡尔树是这样一个二叉树，它能保持原序列的先后顺序，并且具备堆的性质。这里假设序列中无相等元素。

假设有一个序列{9，3，7，1，8，12，10，20，15，18，5}，以此序列来建立一个笛卡尔树，则建好后的二叉树，中序访问该二叉树仍会得到原来的序列{9，3，7，1，8，12，10，20，15，18，5}，且该二叉树还是一个堆（大根堆或小根堆）。以小根堆为例，则建成的笛卡尔树如图所示：

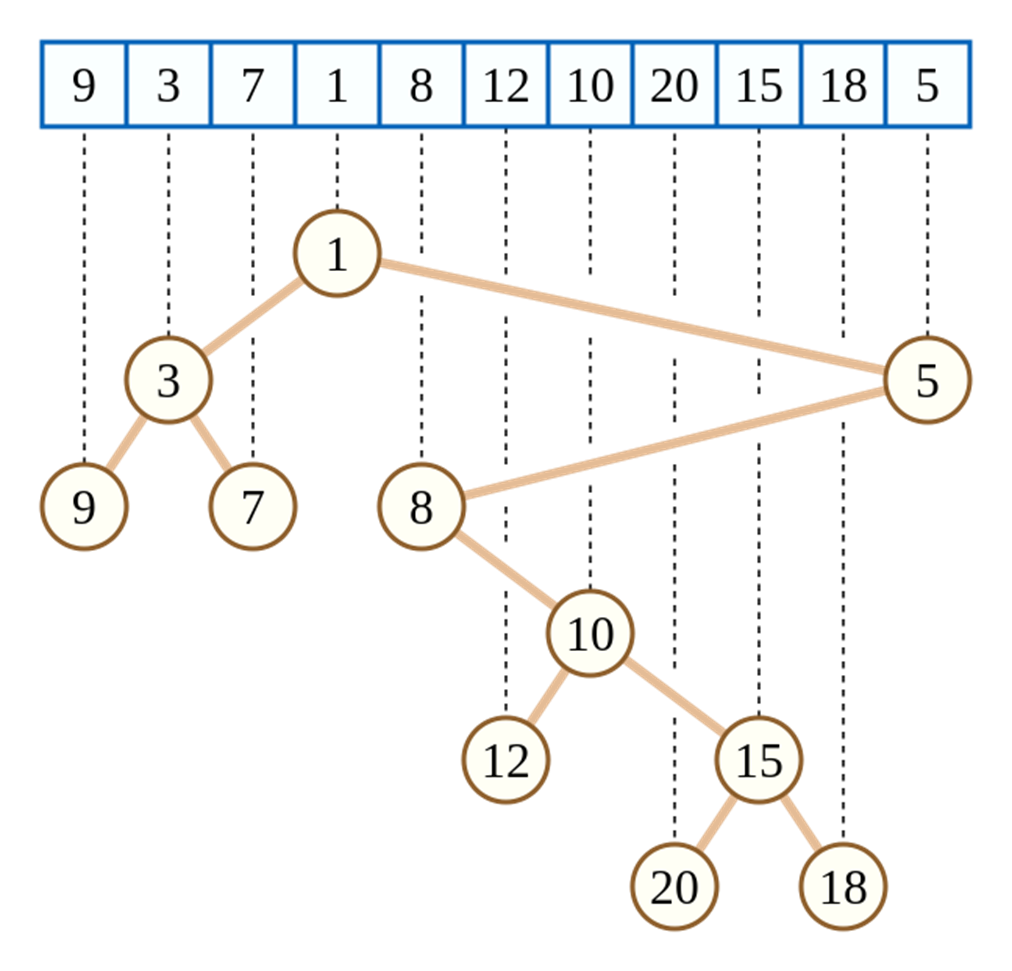
图源自维基百科

来说一下根据指定序列，建立笛卡尔树的思路：

因为新加入的节点在顺序上排在后面，所以只能在树的“右链”中寻找新节点应该插入的位置。（对右链操作的详细解释，可以看https://oi-wiki.org/ds/cartesian-tree/）那么怎么找到合适的位置？最简单的情况：新的节点的值大于右链中的叶子节点