第7章 n步时序差分(2) n步sarsa

n步sarsa

[!NOTE]

复习

SARSA（State–Action–Reward–State–Action）是一种 on-policy（同策略）的时序差分强化学习算法，用于学习在给定策略 $\pi$ 下的动作价值函数（Q 函数）。目标是估计在当前策略 $\pi$ 下，从状态 $s$ 采取动作 $a$ 的预期累积回报，即 $Q^{\pi }(s,a)$。通过在线交互不断更新 $Q$ 值，使得 $Q(s,a)$ 逐渐逼近真实值。

SARSA 基于 TD(0) 更新规则，其更新公式如下：

$$Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha \left[r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)\right]$$

其中：

• $s_t$：当前状态
• $a_t$：当前采取的动作（由当前策略 $\pi$ 选择）
• $r_{t+1}$：执行动作 $a_t$ 后获得的即时奖励
• $s_{t+1}$：执行动作后进入的下一个状态
• $a_{t+1}$：在 $s_{t+1}$ 下根据当前策略 $\pi$ 选择的下一个动作
• $\alpha \in (0,1]$：学习率
• $\gamma \in [0,1)$：折扣因子

SARSA 在更新时使用的是实际采取的下一个动作 $a_{t+1}$，而不是贪心选择的动作。

定义

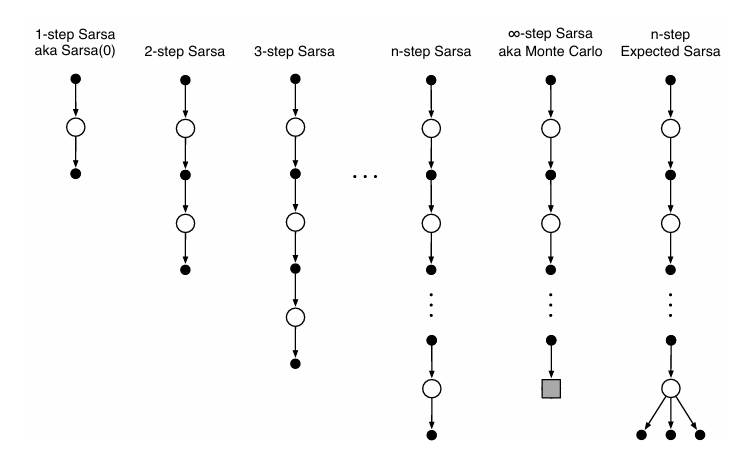
n 步 Sarsa 是将 n 步时序差分方法与 Sarsa 算法结合，形成一种同轨策略下的控制方法。它扩展了原始的单步 Sarsa（即 Sarsa(0)），通过引入多步回报来加速学习关键在于将基本单元从“状态”变为“状态-动作”二元组；使用 ε-贪心策略进行动作选择；回溯图首尾均为动作（区别于状态价值方法）

对于 $ n \geq 1 $ 且 $ 0 \leq t < T - n $，n 步回报定义为：

$$G_{t:t+n}\doteq R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{n-1}{R}_{t+n}+{\gamma }^n{Q}_{t+n-1}(S_{t+n},A_{t+n})$$

当 $ t + n \geq T $ 时，使用完整回报：$ G_{t:t+n} = G_t $

仅更新当前经历的“状态-动作”对：

$$Q_{t+n}(S_t,A_t)\doteq Q_{t+n-1}(S_t,A_t)+\alpha \left[G_{t:t+n}-Q_{t+n-1}(S_t,A_t)\right]$$

其余所有 $ (s, a) \neq (S_t, A_t) $ 的 Q 值保持不变。

算法实现

输入：无显式输入策略（策略由 Q 函数隐式定义）
参数：步长 $\alpha \in (0,1]$，探索率 $\epsilon >0$，正整数 $n$
初始化：对所有 $s\in \mathcal{S},a\in \mathcal{A}(s)$，任意初始化 $Q(s,a)$；策略 $\pi$ 为基于当前 $Q$ 的 ε-贪心策略

对每幕执行：

1. 初始化并存储初始状态 $S_0$（非终止状态）

2. 根据 $\pi (\cdot \mid S_0)$ 选择并存储动作 $A_0$

3. 设 $T\leftarrow \infty$

4. 对 $t=0,1,2,\dots$ 执行：

   • 若 $t<T$：

     • 执行动作 $A_t$
     • 观察并存储奖励 $R_{t+1}$ 和下一状态 $S_{t+1}$
     • 若 $S_{t+1}$ 为终止状态，则 $T\leftarrow t+1$
     • 否则，根据 $\pi (\cdot \mid S_{t+1})$ 选择并存储动作 $A_{t+1}$

   • 计算 $\tau \leftarrow t-n+1$

   • 若 $\tau \ge 0$：

     • 计算部分回报：
       $$G\leftarrow \sum _{i=\tau +1}^{\min (\tau +n,T)}{\gamma }^{i-\tau -1}{R}_i$$

     • 若 $\tau +n<T$，追加自举项：
       $$G\leftarrow G+{\gamma }^{n}Q(S_{\tau +n},A_{\tau +n})$$

     • 更新动作价值函数：
       $$Q(S_{\tau },A_{\tau })\leftarrow Q(S^{}$$