【C++】红黑树

红黑树的概念

红黑树是一种二叉搜索树，单在每个节点上增加一个储存为表示节点的颜色，可以是RED或BLACK。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而接近平衡。

近似平衡

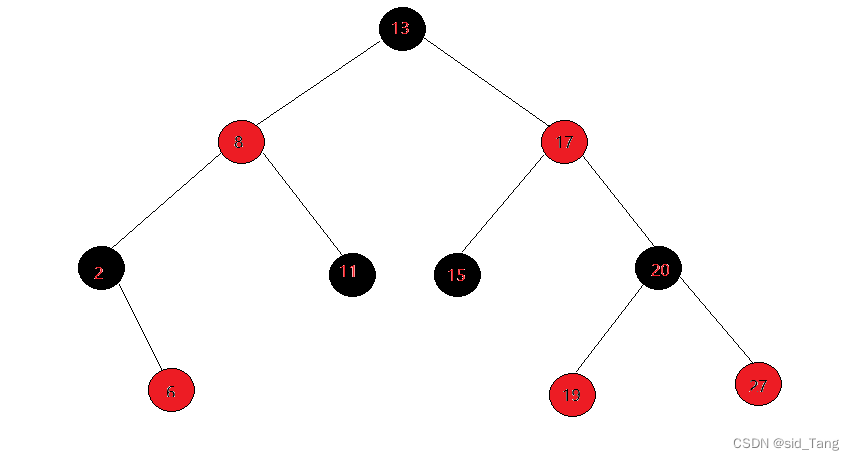
最长路径不超过最短路径两倍近似平衡

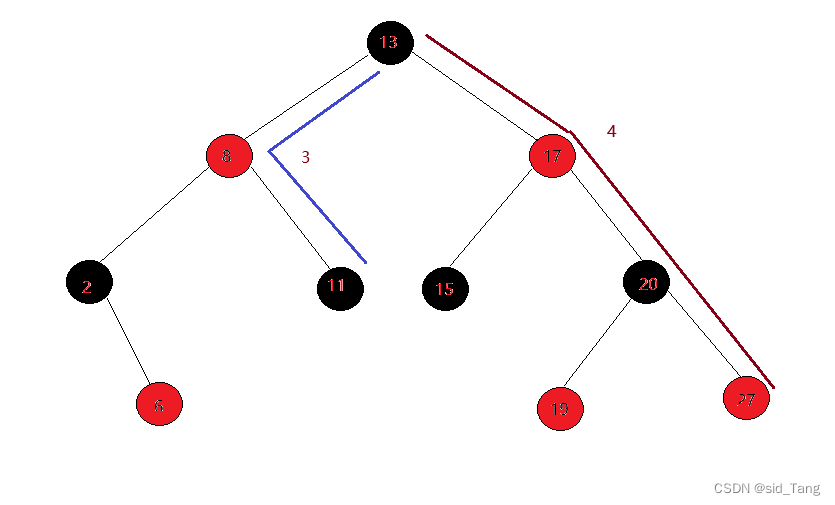
红黑树的性质

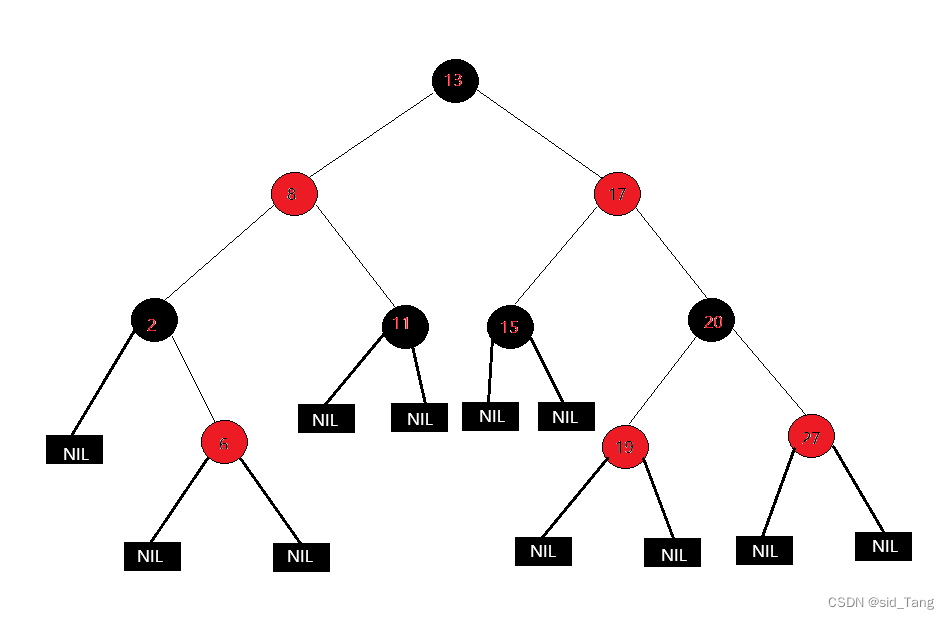
1.每个节点不是红色就是黑色
2.根节点必须是黑色

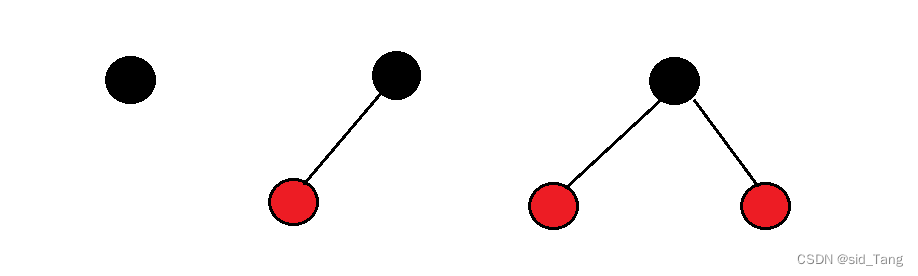
3.如果一个节点是红色的，则它的两个孩子节点必须是黑色.任何路径都没有连续的红色结点
4.对于每个结点，从该节点到其所有的后代叶子结点的简单路径上，均包含相同数目的黑色结点。每条路径上黑色结点的数量相等。

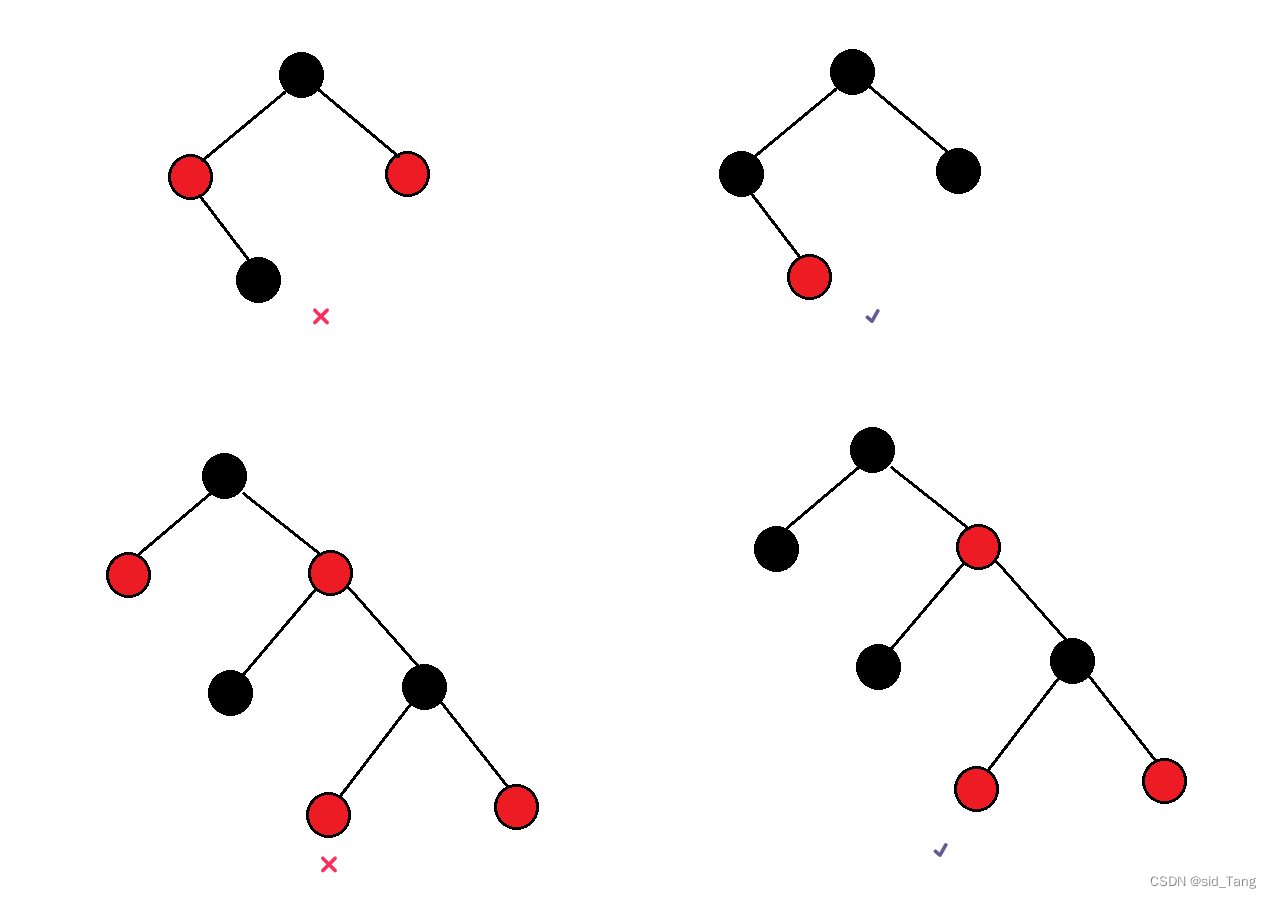
5.每个叶子结点都是黑色的（此处的叶子结点是指空结点，也就是NIL结点）

AVL树和红黑树的对比

性能是同一量级的，但是AVL树，控制严格平衡是付出代价的，插入和删除时需要进行大量的旋转。

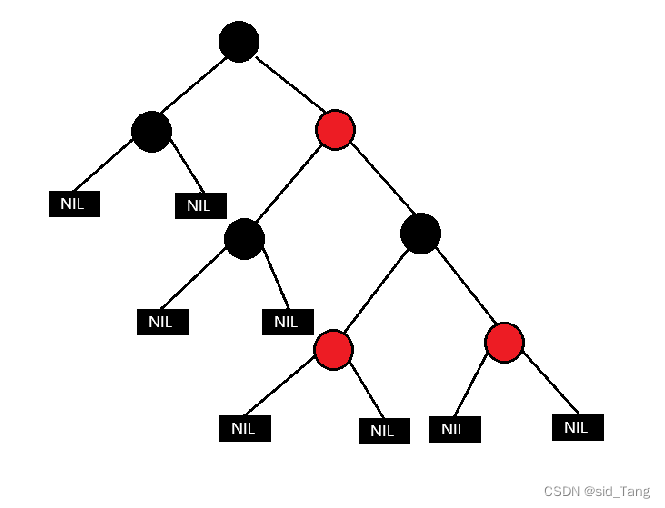
红黑树新节点插入

所有插入的新节点默认为红色

检测新节点是否破坏红黑树的性质

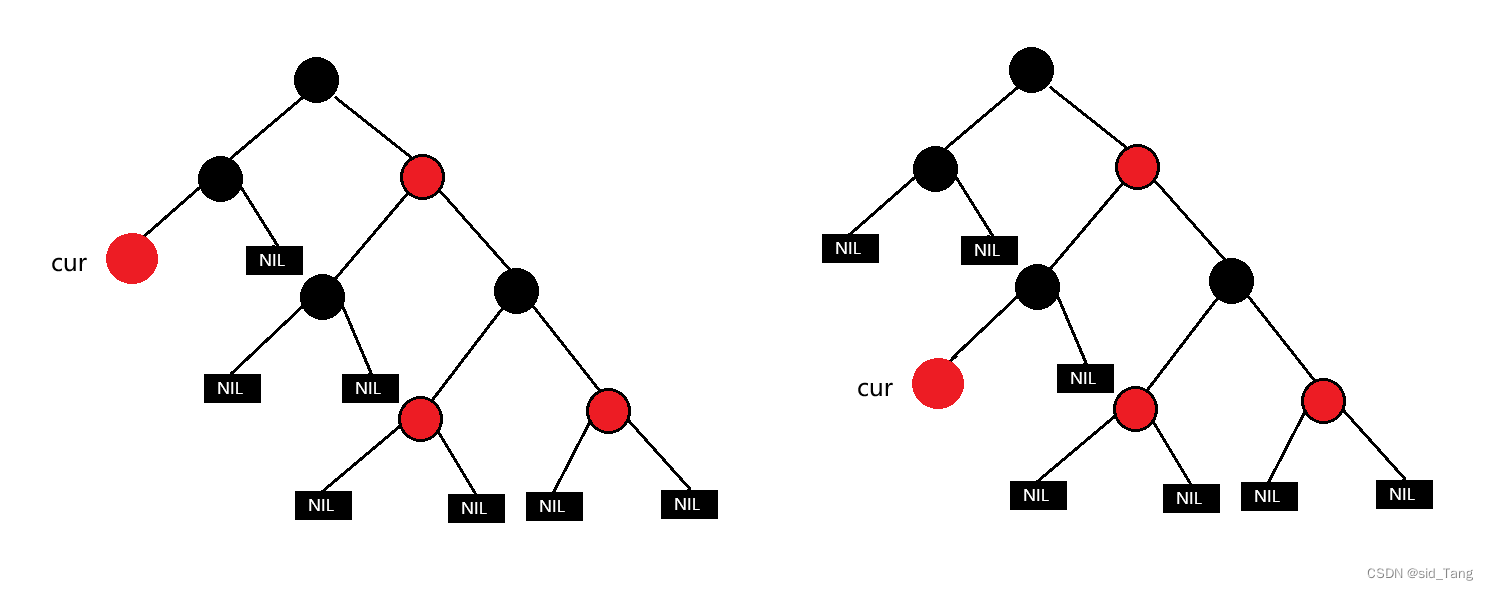
新节点最长路径没有超过最短路径的两倍，没有连续的红色结点，每条路径的黑色结点数量相同则不影响。

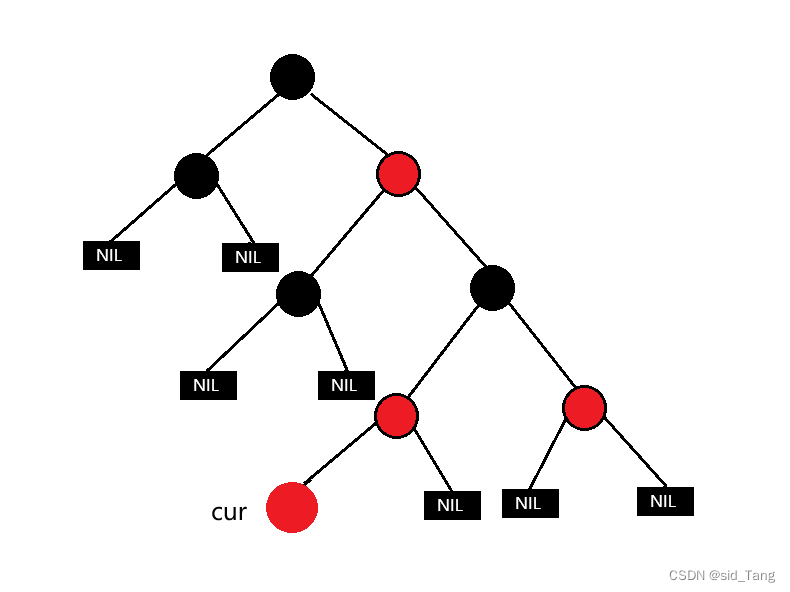
新增结点破坏了红黑树的性质。

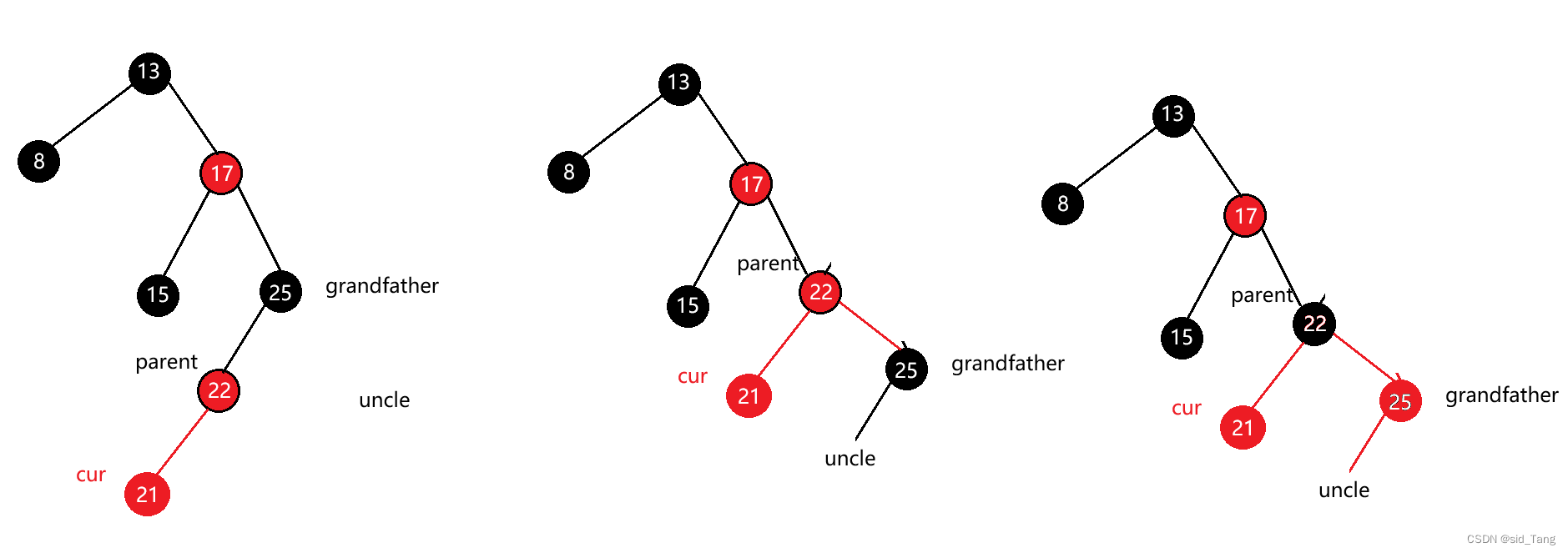
情况一：cur为红，parent为红，grandfather为黑，uncle存在且为红

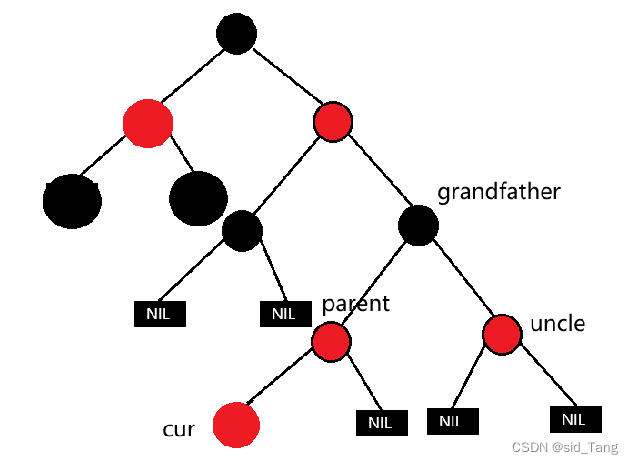
情况一，可能是一颗完整的树，也可能是一颗子树

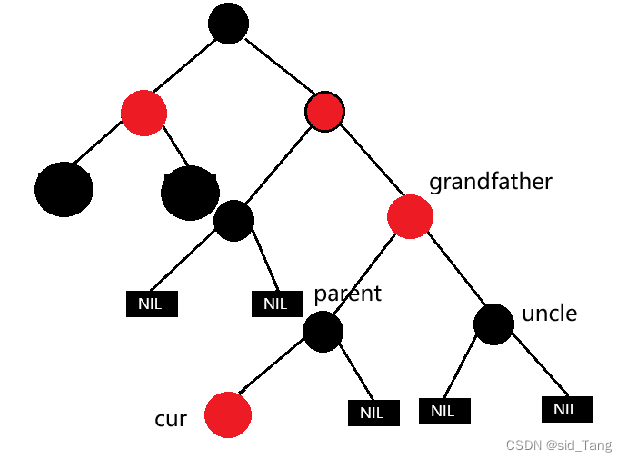
如果grandfather是根，调整完成后需要讲grandfather改为黑色
如果grandfather是子树，grandfather一定有双亲，且grandfather的双亲如果是红色，需要继续向上调整

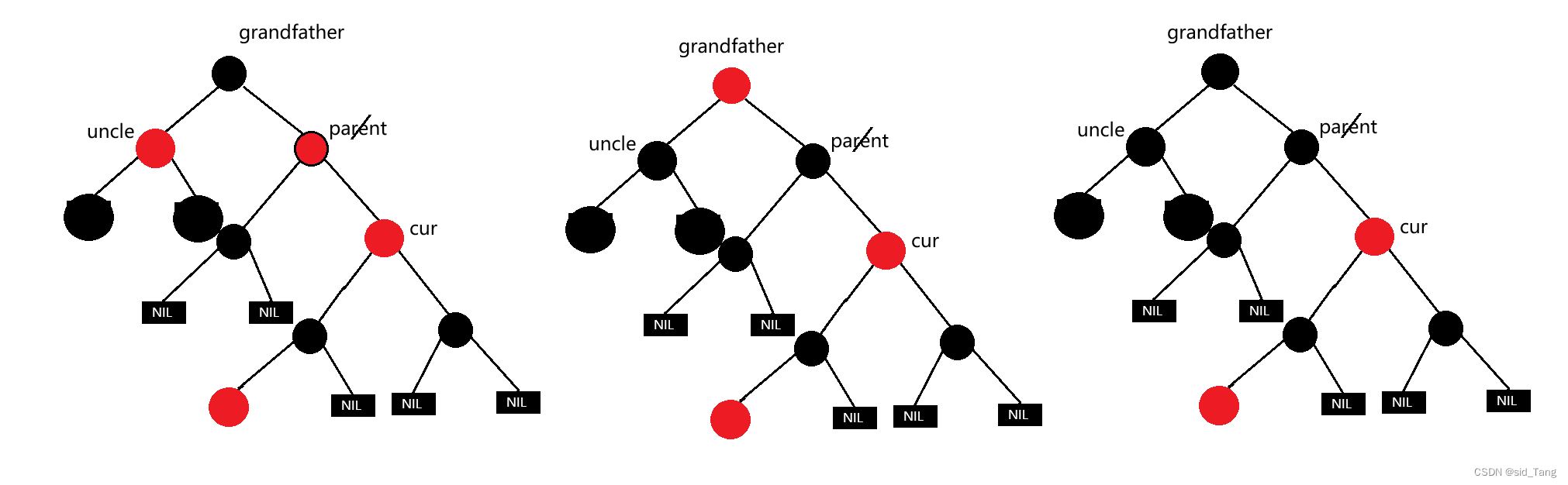
解决方式：讲parent和uncle改为黑，grandfather改为红，然后grandfather变为cur继续向上调整

情况二：cur为红，parent为红，grandfather为黑，uncle不存在或uncle存在且为黑

cur为红，parent为红，grandfather为黑，uncle不存在

如果uncle结点不存在，则cur一定是新插入的结点，因为如果cur不是新插入的结点，则cur和parent一定有一个结点的颜色是黑色，就不满足性质4：每条路径黑色结点个数相同

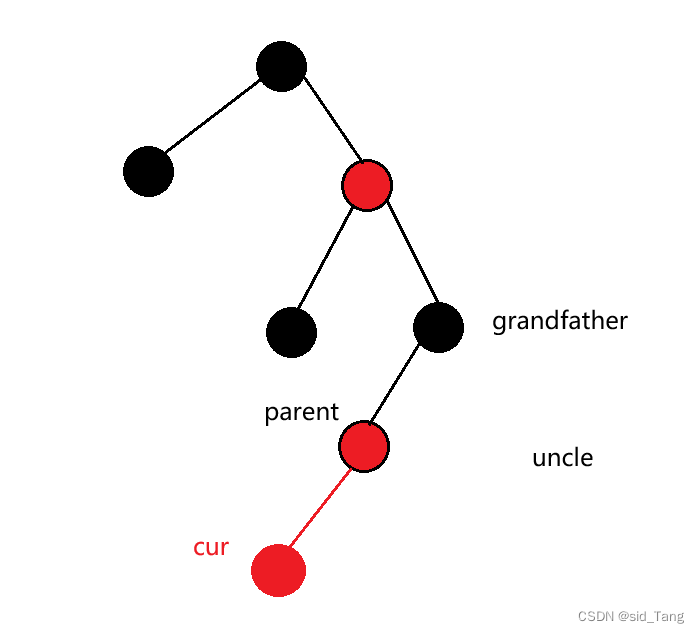
此上情况则需要旋转加变色

parent == grandfather->left;
cur == parent->left;

进行右单旋

grandfather->left = parent->right;
parent->right = grandfather;

然后改色

grandfather->color = RED;
parent->color = BLACK;

cur为红，parent为红，grandfather为黑，uncle存在且为黑

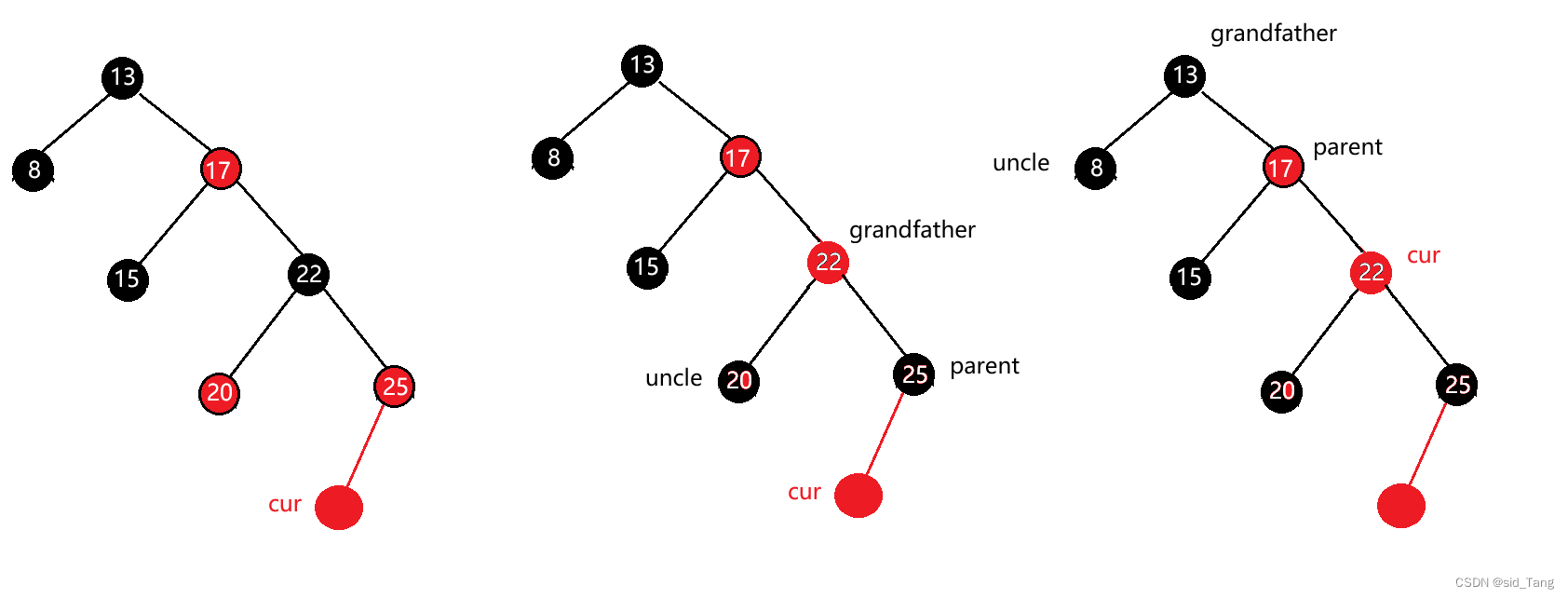
进行旋转加变色。
如果parent是grandfather的右孩子，cur为parent的右孩子，则针对parent做左单旋。
如果parent为grandfather的左孩子，cur为parent的左孩子，则针对parent进行右单旋。

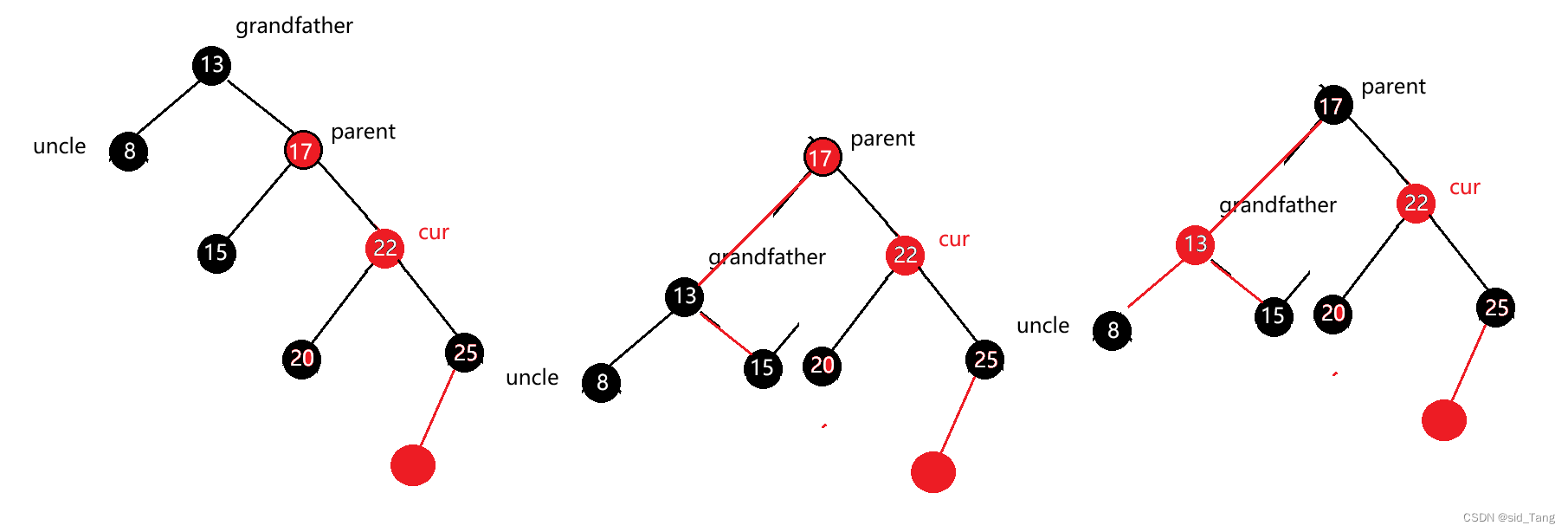
uncle->color == BLACK;
grandfather->right == parent;
parent->right == cur;
grandfather->right = parent->left;
parent->left = grandfather

parent->color = BLACK;
grandfather->color = RED;