CodeForces 599A Patrick and Shopping （商店购物最短路程）

最新推荐文章于 2019-02-09 14:13:34 发布

Shyazhut

最新推荐文章于 2019-02-09 14:13:34 发布

阅读量556

点赞数

CC 4.0 BY-SA版权

分类专栏： CodeForces 一块水过这的题

本文链接：https://blog.youkuaiyun.com/shyazhut/article/details/52000081

一块水过这的题同时被 2 个专栏收录

144 篇文章

订阅专栏

CodeForces

124 篇文章

订阅专栏

本文介绍了一道关于寻找从家出发到两个商店购物并返回家中最短路径的问题。通过列举所有可能的行走路线，对比计算得出最短路径。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Today Patrick waits for a visit from his friend Spongebob. To prepare for the visit, Patrick needs to buy some goodies in two stores located near his house. There is a d1 meter long road between his house and the first shop and a d2 meter long road between his house and the second shop. Also, there is a road of length d3 directly connecting these two shops to each other. Help Patrick calculate the minimum distance that he needs to walk in order to go to both shops and return to his house.

$\text{[math]}$

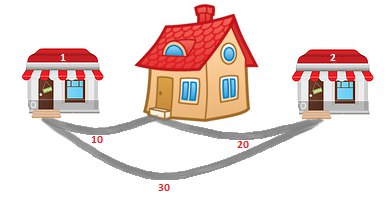
Patrick always starts at his house. He should visit both shops moving only along the three existing roads and return back to his house. He doesn't mind visiting the same shop or passing the same road multiple times. The only goal is to minimize the total distance traveled.

Input

The first line of the input contains three integers d1, d2, d3 (1 ≤ d1, d2, d3 ≤ 108) — the lengths of the paths.

d1 is the length of the path connecting Patrick's house and the first shop;
d2 is the length of the path connecting Patrick's house and the second shop;
d3 is the length of the path connecting both shops.

Output

Print the minimum distance that Patrick will have to walk in order to visit both shops and return to his house.

        Examples
      
          input
        
10 20 30

          output
        
60

          input
        
1 1 5

          output
        
4

Note

The first sample is shown on the picture in the problem statement. One of the optimal routes is: house $\text{[math]}$ first shop $\text{[math]}$ second shop $\text{[math]}$ house.

In the second sample one of the optimal routes is: house $\text{[math]}$ first shop $\text{[math]}$ house $\text{[math]}$ second shop $\text{[math]}$ house.

题意：

你在自己的家里，需要外出到两个商店分别买一个东西，最后再回家敲代码。

输出最节省路程的方案。

思路：

A: 自己的房子 B:左边的商店 C:右边的商店

例举出全部的方案就可以了。（看代码注释部分）

代码：

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<string.h>
#include<algorithm>
#define MYDD 66

using namespace std;

int MIN(int x,int y) {
	return x<y? x:y;
}

int main() {
	int ans,d1,d2,d3,min;
	// A: 家 B:第一个商店 C: 第二个商店
	while(scanf("%d%d%d",&d1,&d2,&d3)!=EOF) {
		ans=d1+d2+d3;//ABCA
		min=ans;
		ans=2*(d1+d3);//ABCBA
		min=MIN(ans,min);
		ans=2*(d2+d3);//ACBCA
		min=MIN(ans,min);
		ans=2*(d2+d1);//ABACA 或者 ACABA 
		min=MIN(ans,min);
		printf("%d\n",min);
	}
	return 0;
}

/*
 
*/