【数据结构笔记】1数组内存模型(随机访问行优先列优先 Openjdk数组操作)

最新推荐文章于 2021-12-06 21:47:43 发布

shuzip

最新推荐文章于 2021-12-06 21:47:43 发布

阅读量1.3k

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构

本文链接：https://blog.youkuaiyun.com/shuzip/article/details/104655559

数据结构专栏收录该内容

2 篇文章

订阅专栏

本文深入探讨数组的内存模型，包括一维、二维及多维数组的行优先与列优先存储方式，分析数组随机访问特性及时间复杂度。同时，通过Java源码分析，揭示动态数组插入删除操作的时间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数组（Array）。

数组的内存模型

1.一维数组

在计算机科学中，数组可以被定义为是一组被保存在连续存储空间中，并且具有相同类型的数据元素集合。而数组中的每一个元素都可以通过自身的索引（Index）来进行访问。

以 Java 语言中的一个例子来说明一下数组的内存模型，当定义了一个拥有 5 个元素的 int 数组后，。

int[] data = new int[5];

通过上面这段声明，计算机会在内存中分配一段连续的内存空间给这个 data 数组。现在假设在一个 32 位的机器上运行这段程序，Java 的 int 类型数据占据了 4 个字节的空间，同时也假设计算机分配的地址是从 0x80000000 开始的，整个 data 数组在计算机内存中分配的模型如下图所示。

在这里插入图片描述
（图一）

这种分配连续空间的内存模型同时也揭示了数组在数据结构中的另外一个特性，即随机访问（Random Access）。随机访问这个概念在计算机科学中被定义为：可以用同等的时间访问到一组数据中的任意一个元素。这个特性除了和连续的内存空间模型有关以外，其实也和数组如何通过索引访问到特定的元素有关。

在访问数组中的第一个元素时，程序一般都是表达成以下这样的：

data[0]

也就是说，数组的第一个元素是通过索引“0”来进行访问的，第二个元素是通过索引“1”来进行访问的，……，这种从 0 开始进行索引的编码方式被称为是“Zero-based Indexing”。当然，在计算机世界中也存在着其他的索引编码方式，像 Visual Basic 中的某些函数索引是采用 1-based Indexing 的，也就是说第一个元素是通过“1”来获取的，

我们回到数组中第一个元素通过索引“0”来进行访问的问题上来，之所以采取这样的索引方式，原因在于，获取数组元素的方式是按照以下的公式进行获取的：

base_address + index（索引）× data_size（数据类型大小）

索引在这里可以看作是一个偏移量（Offset），还是以上面的例子来进行说明。
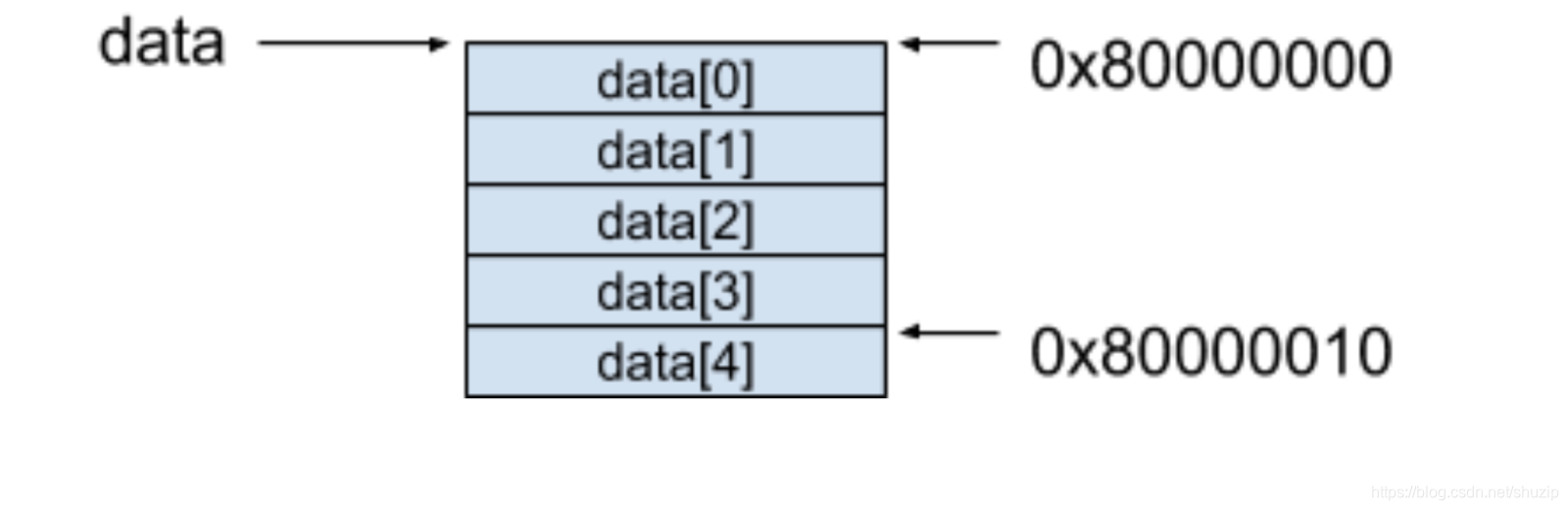
在这里插入图片描述

（图二）

data 这个数组被分配到的起始地址是 0x80000000，是因为 int 类型数据占据了 4 个字节的空间，如果我们要访问第 5 个元素 data[4] 的时候，按照上面的公式，只需要取得 0x80000000 + 4 × 4 = 0x80000010 这个地址的内容就可以了。随机访问的背后原理其实也就是利用了这个公式达到了同等的时间访问到一组数据中的任意元素。

2.二维数组

上面所提到的数组是属于一维数组的范畴，我们平时可能还会听到一维数组的其他叫法，例如，向量（Vector）或者表（Table）。因为在数学上，二维数组可以很好地用来表达矩阵（Matrix）这个概念，所以很多时候我们又会将矩阵或者二维数组这种称呼交替使用。

如果我们按照下面的方式来声明一个二维数组：

int[][] data = new int[2][3];

在面试中，如果我们知道了数组的起始地址，在基于上面的二维数组声明的前提下，data[0][1] 这个元素的内存地址是多少呢？标准的答案其实应该是“无法确定”。什么？标准答案是无法确定，别着急，因为这个问题的答案其实和二维数组在内存中的寻址方式有关。而这其实涉及到计算机内存到底是以行优先（Row-Major Order）还是以列优先（Column-Major Order）存储的。

假设现在有一个二维数组，如下图所示
在这里插入图片描述
（图三）

下面我们来一起看看行优先或列优先的内存模型会造成什么样的区别。

（1）行优先

行优先的内存模型保证了每一行的每个相邻元素都保存在了相邻的连续内存空间中，对于上面的例子，这个二维数组的内存模型如下图所示，假设起始地址是 0x80000000：
在这里插入图片描述
（图四）

可以看到，在二维数组的每一行中，每个相邻元素都保存在了相邻的连续内存里。

在以行优先存储的内存模型中，假设我们要访问 data[i][j] 里的元素，获取数组元素的方式是按照以下的公式进行获取的：

base_address + data_size × (i × number_of_column + j)

回到一开始的问题里，当我们访问 data[0][1] 这个值时，可以套用上面的公式，其得到的值，就是我们要找的 0x80000004 地址的值，也是就 2。

0x80000000 + 4 × (0 × 3 + 1) = 0x80000004

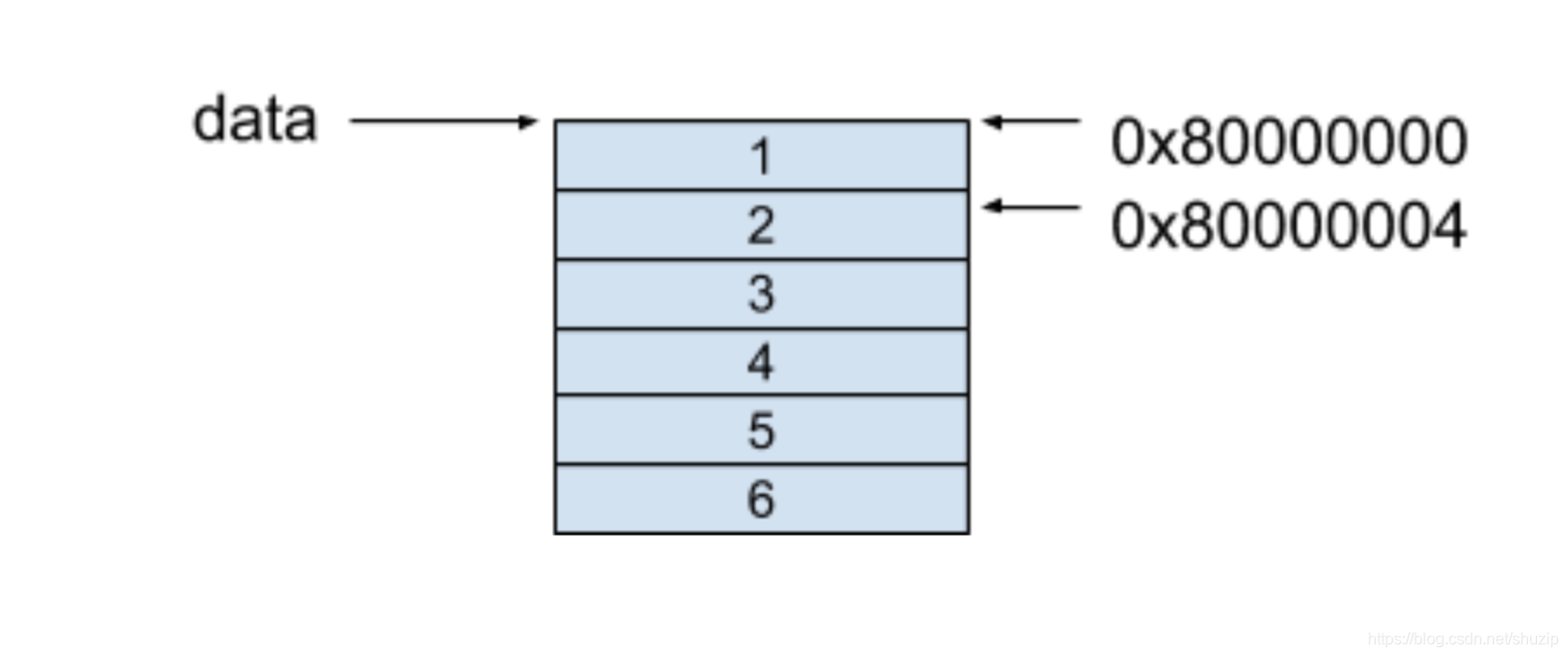
在这里插入图片描述
（图五）

（2）列优先

列优先的内存模型保证了每一列的每个相邻元素都保存在了相邻的连续内存中，对于上面的例子，这个二维数组的内存模型如下图所示，我们同样假设起始地址是 0x80000000：
在这里插入图片描述
（图六）

可以看到，在二维数组的每一列中，每个相邻元素都保存在了相邻的连续内存里。

在以列优先存储的内存模型中，假设我们要访问 data[i][j] 里的元素，获取数组元素的方式是按照以下的公式进行获取的：

base_address + data_size × (i + number_of_row × j)

当我们访问 data[0][1] 这个值时，可以套用上面的公式，其得到的值，就是我们要找的 0x80000008 地址的值，同样也是 2。

0x80000000 + 4 × (0 + 2×1) = 0x80000008

在这里插入图片描述
（图七）

所以回到一开始的那个面试问题里，行优先还是列优先存储方式会造成 data[0][1] 元素的内存地址不一样。

3.多维数组

多维数组其实本质上和前面介绍的一维数组和二维数组是一样的。如果我们按照下面的方式来声明一个三维数组：

int[][][] data = new int[2][3][4];

则可以把这个声明想象成声明了两个 int[3][4] 这样的二维数组，对于多维数组则可以以此类推。下面我将把行优先和列优先的内存寻址计算方式列出来，若感兴趣的话可以将上面所举的二维数组例子套入公式，自行验证一下。

假设我们声明了一个 data[S1][S2][S3]…[Sn] 的多维数组，如果我要访问 data[D1][D2][D3]…[Dn] 的元素，内存寻址计算方式将按照如下方式寻址：

行优先

base_address + data_size × (Dn + Sn × (Dn-1 + Sn-1 × (Dn-2 + Sn-2 × (... + S2 × D1)...)))

列优先

base_address + data_size × (D1 + (S1 × (D2 + S2 × (D3 + S3 × (... + Sn-1 × Dn)...)))

虽然行优先或是列优先这种内存模型对于我们工程师来说是透明的，但是如果我们掌握好了哪种高级语言是采用哪种内存模型的话，这就对于我们来说是很有用的。

CPU 在读取内存数据的时候，通常会有一个 CPU 缓存策略。也就是说，在 CPU 读取程序指定地址的数值时，CPU 会把和它地址相邻的一些数据也一并读取并放到更高一级的缓存中，比如 L1 或者 L2 缓存。当数据存放在这种缓存上的时候，读取的速度有可能会比直接从内存上读取的速度快 10 倍以上。

如果知道了数据存放的内存模型是行优先的话，在设计数据结构的时候，会更倾向于读取每一行上的数据，因为每一行的数据在内存中都是保存在相邻位置的，它们更有可能被一起读取到 CPU 缓存中；反之，我们更倾向于读取每一列上的数据。

那高级语言中有哪些是行优先又有哪些是列优先呢？我们常用的 C/C++ 和 Objective-C 都是行优先的内存模型，而 Fortran 或者 Matlab 则是列优先的内存模型。

“高效”的访问与“低效”的插入删除

从前面的数组内存模型的学习中，我们知道了访问一个数组中的元素采用的是随机访问的方式，只需要按照上面讲到的寻址方式来获取相应位置的数值便可，所以访问数组元素的时间复杂度是 O(1)。

对于保存基本类型（Primitive Type）的数组来说，它们的内存大小在一开始就已经确定好了，我们称它为静态数组（Static Array）。静态数组的大小是无法改变的，所以我们无法对这种数组进行插入或者删除操作。但是在使用高级语言的时候，比如 Java，我们知道 Java 中的 ArrayList 这种 Collection 是提供了像 add 和 remove 这样的 API 来进行插入和删除操作，这样的数组可以称之为动态数组（Dynamic Array）。

我们来一起看看 add 和 remove 函数在 Java Openjdk-jdk11 中的源码，一起分析它们的时间复杂度。

在 Java Collection 中，底层的数据结构其实还是使用了数组，一般在初始化的时候会分配一个比我们在初始化时设定好的大小更大的空间，以方便以后进行增加元素的操作。

假设所有的元素都保存在 elementData[] 这个数组中，add 函数的主要时间复杂度来自于以下源码片段。

1.add(int index, E element) 函数源码

首先来看看 add(int index, E element) 这个函数的源码。 (点击这里查看源代码)

public void add(int index, E element) {
    ...
    System.arraycopy(elementData, index,
                     elementData, index + 1,
                     s - index);
    elementData[index] = element;
    ...
}

可以看到，add 函数调用了一个 System.arraycopy 的函数进行内存操作，s 在这里代表了 ArrayList 的 size。当我们调用 add 函数的时候，函数在实现的过程中到底发生了什么呢？我们来看一个例子。

假设 elementData 里面存放着以下元素：

在这里插入图片描述
（图八）

如果我们调用了 add(1, 4) 函数，也就是在 index 为 1 的地方插入 4 这个元素，在 add 的函数中则会执行 System.arraycopy(elementData, 1, elementData, 2, 6 - 1) 语句，它的意思是将从 elementData 数组 index 为 1 的地址开始，复制往后的 5 个元素到 elementData 数组 index 为 2 的地址位置，如下图所示：

在这里插入图片描述
（图九）

红色的部分代表着执行完 System.arraycopy 函数的结果，最后执行 elementData[1] = 4; 这条语句：

在这里插入图片描述
（图十）

因为这里涉及到了每个元素的复制，平均下来的时间复杂度相当于 O(n)。

2.remove(int index) 函数源码

同理，我们来看看 remove(int index) 这个函数的源码。（点击这里查看源代码）

public void remove(int index) {
    ...
    fastRemove(es, index);
    ...
}
 
private void fastRemove(Object[] es, int i) {
    ...
    System.arraycopy(es, i + 1, es, i, newSize - i);
    ...
}

这里的 newSize 是指原来 elementData 的 size - 1，当我们调用 remove(1) 会发生什么呢？我们还是以下面的例子来解释。
在这里插入图片描述

（图十一）

如果我们调用了 remove(1) 函数，也就是删除在 index 为 1 这个地方的元素，在 remove 的函数中则会执行 System.arraycopy(elementData, 1 + 1, elementData, 1, 2) 语句，它的意思是将从 elementData 数组 index 为 2 的地址开始，复制后面的 2 个元素到 elementData 数组 index 为 1 的地址位置，如下图所示：
在这里插入图片描述