学习笔记-1-Review of Linear Algebra-1-Vector

最新推荐文章于 2025-12-15 15:14:09 发布

原创最新推荐文章于 2025-12-15 15:14:09 发布 · 279 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#学习 #算法

数据科学专栏收录该内容

10 篇文章

订阅专栏

细节内容请关注微信公众号：运筹优化与数据科学

ID: pomelo_tree_opt

第一部分是对vector和matrix的深入理解，尤其是从data的角度，从machine learning的角度，去理解

(1) vector和matrix到底是个什么东西
(2) 为什么要引入这两个东西
(3) vector和matrix可以有什么操作，这些操作又分别代表什么含义

------------------------------

首先是一些符号标准

通用的符号标准可以让我们不会花费时间在无谓的事情上

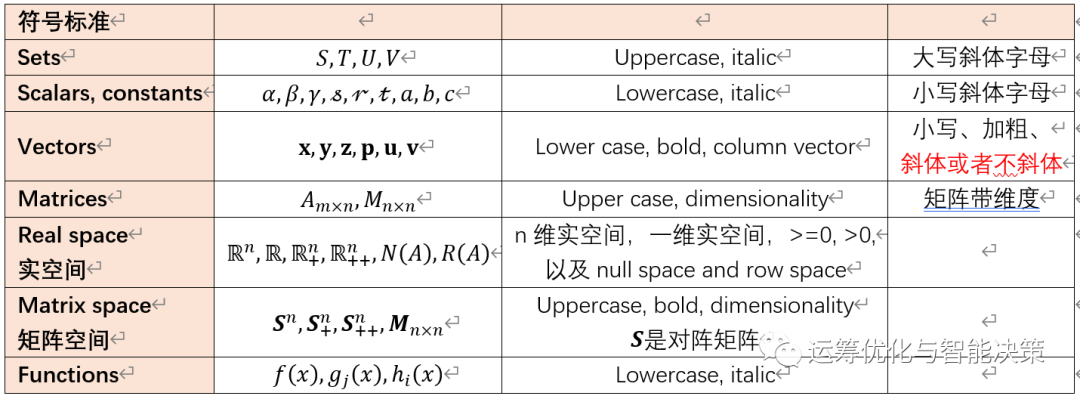
Outline

向量的基本认识
两个向量之间的关系
一堆向量之间的关系

---------------------------------

1. Vector向量的基本认识

Vector就是个带方向的量，或者一个几何对象geometric object with magnitude (or length) and direction. 先有标量scalar, 然后再有向量(矢量)vector, 再是矩阵Matrix, 好像再之后是Tensor.

-------------------------------------

关于向量方向的理解

一个向量，比如二维向量，本身的代表二维平面上的一个点，就是从(0, 0)点到该点的一个指向。
给定两个向量h, t, then v=h-t, 就是从tail到head的一个向量。

------------------------------------

关于向量长度的理解

长度就是magnitude, length, size, 其实就是norm范数。

------------------------------------

单位向量

一个向量除以它的长度, 就会得到沿该向量方向的一个单位向量unit vector, 这个操作也叫做normalize, 标准化或规范化。就是变成一个单位长度的向量。

对于单位向量而言，几何上从尾走到头，只需要走1步，1个单位，单位长度的向量。（这一点在计算两个hyperplane之间的距离时有用到）

------------------------------------

向量范数norm的概念

magnitude, size, length, norm都是差不多的概念。

说明

0-阶范数，是一个值的问题，存在几个非零的元素。坐标形式中有几个不为0的。
1-阶范数，是坐标形式中的各个坐标的绝对值，1阶范数也叫做rectangular norm, 因为它的表现形式就是个类似矩形的东西，有点像个box
2-阶范数，也叫做欧式范数，Euclidean norm, 是我们最常见的距离的计算方式
p-阶范数，绝对值的p次方求和，再开p次方根。
inf-阶范数，找一个最大的绝对值。

0阶范数是个值的问题，1--阶范数都是量的问题。

---------------------------------

为什么会有不同的norm，是因为每个norm的功能不同，特性不同

0-norm其实就是cardinality, “基数”，“势”，也就是非零元素的个数。
1-norm对处理outlier异常值时，异常值对平均表现的影响最小，“平平整整”
2-norm就需要花费很多力气来处理outlier,会导致波动很明显，“上上下下”

有一部分在讲support vector regression的时候，有个robust的概念，就是用1-norm来代替2-norm，为了减轻或削弱“异常值”的影响。

---------------------------------

几个思考问题

1. What is the role of vectors in machine learning?

2. How are two given vectors u, v related? Any implications?

3. How to find a vector w orthogonal to a given vector u?

4. Can you find a third vector s that is orthogonal to both of u and w?

---------------------------------

1. What is the role of vectors in machine learning?

一个向量就类似于一个data record, 向量有很多维度，类比data有很多属性。换句话说，一个向量就是一条记录；一大堆data的中的某一条，就是一个vector.

如果没有特殊说明，向量都是指列向量，竖着摆的。

---------------------------------

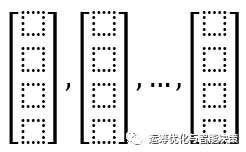
2. How are two given vectors u, v related? Any implications

两个向量之间的关系是通过它们的操作来体现的。向量有一些基本操作，比如一个向量乘一个标量，两个向量相加，两个向量的内积(点积)

向量*标量从几何上看，可以看作是向量在伸缩。
两个向量的加减，从几何上看是在构造另外一个向量，按照那个平行四边形法则的计算方式
内积（或点积），是相对而言最特殊的，内积是用来描述两个向量之间的关系，两个向量是否相关，有多相关等。
两个向量的关系最特殊、最重要的就是“正交”这种关系，正交就是内积为0

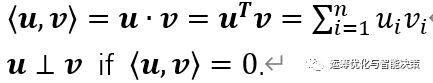
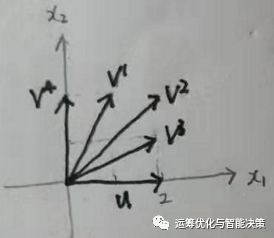
可以简单理解，两个向量的内积越大表示两者越相关，相关性越高。

例如，这个例子中，u和v1的相关性，就不如u和v2的相关性高。最特殊的正交是u和v4的关系，内积为0，表示两者完全不相关。

再严谨点，其实应该是先把两个向量normalize一下，再去比较

---------------------------------

3. How to find a vector w orthogonal to a given vector u?

4. Can you find a third vector s that is orthogonal to both of u and w?

3&4其实就是Gram-Schmidt正交化方法，这是一种将矩阵化为标准正交向量矩阵orthonormal matrix的方法。Schimidt教我们如何将一个向量标准化normalized, 而Gram教让我们如何使得各个向量正交orthogonal.

---------------------------------

首先是怎么去寻找“正交”向量，根据内积的几何意义来寻找正交向量。

简单来讲，就是减去在上的投影，就得到了一个垂直于的向量。

---------------------------------

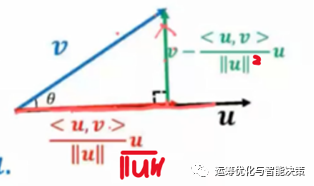
三维的情况

整体的运算过程图形化展示就是下面的样子

------------------------------------

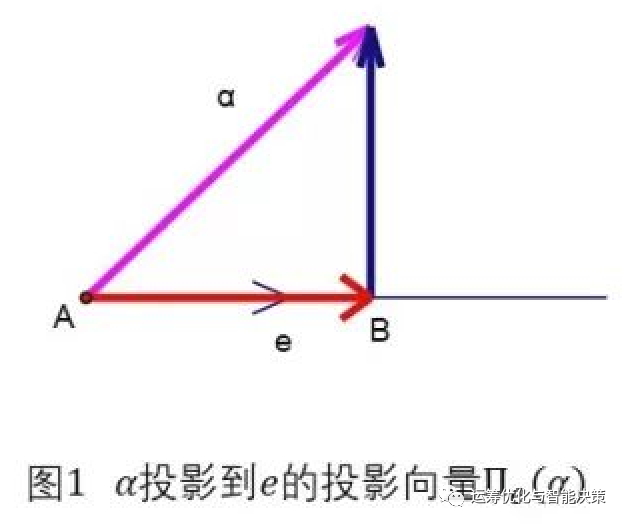
3. 一堆向量之间的关系

前面是两个向量的关系，最重要的就是正交，接下来是一堆向量的关系，一堆向量可以看作是一个集合。很多向量的时候，我们关注的是这堆向量是否是线性独立 linearly independent.

=========================

总结：

一堆资料，就是一堆向量，其中线性独立的向量越多，扩张出来的空间就越大，可以朴素的理解成其中包含的信息越多就行。

换个角度来看，对于一堆资料而言，其实最重要的就是其中linearly independent的那些资料，坚实的资料，这些资料的组合，就可以构成所有的资料。

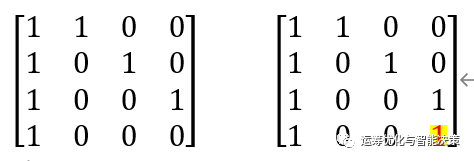
左边是4笔资料，这4笔资料都很重要，因为是linearly independent的。
右边也是4笔资料，这4笔资料不是linearly independent的，因为第1笔资料就可以写成2+3+4的形式。相比之下，第1笔资料就没那么重要了，因为可以用其他的资料组合出来。也可以说，这个集合包含的信息不如上面那个集合包含的信息多。