学习笔记-1-Review of Linear Algebra-2-Matrix-2-Reloaded

细节内容请关注微信公众号：运筹优化与数据科学

ID: pomelo_tree_opt

---

Outline

1. classical matrix

2. matrix operations

3. features of matrix

4. determinant, trace, eigen, definite matrix

-------------------------

首先是一些特殊结构的矩阵

• Square matrix就是方阵，相比于rectangular matrix，方阵有很多特点，

• 对角矩阵，diagonal matrix, 就是只有主对角元素，其他元素均为0

• 上三角矩阵，upper triangular matrix, 就是主对角线下面的元素都是0

• 下三角矩阵，lower triangular matrix, 就是主对角线上面的元素都是0

• 单位矩阵，identity matrix, 就是对角矩阵，且主对角线元素均为1.

• 对称矩阵，symmetric matrix

-------------------------------

一些思考：为什么要关心这些特殊结构？有什么特殊信息隐含在其中吗？或者说这些结果能够帮助我们处理什么问题吗？

这些矩阵能代表一些特殊的含义，一些特殊的变换动作。

-------------------------------

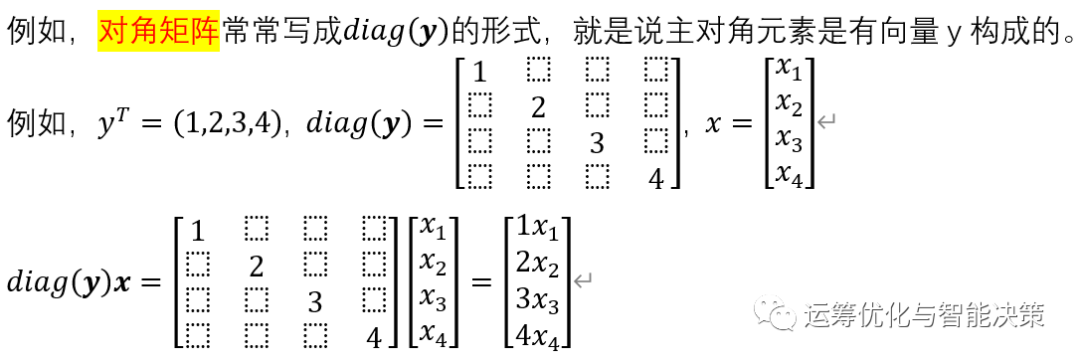
某个向量左乘一个对角矩阵，类似于加权操作，相当于向量x的每个元素都乘了一个系数。

-------------------------------

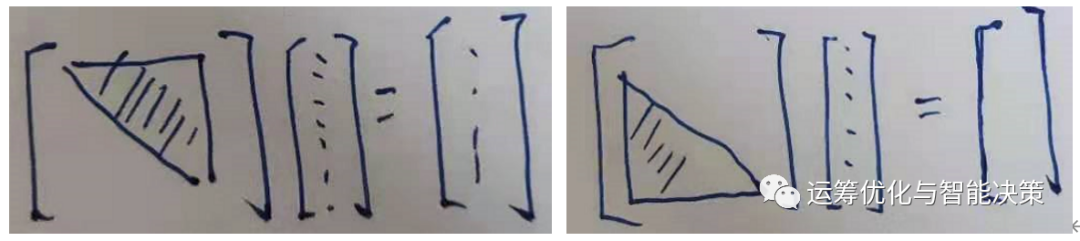
半正定矩阵，可以转化为一个下三角矩阵乘一个上三角矩阵的形式，似乎是把两个方向的内容变成单方向来处理，sequential processing. 

上三角矩阵，或下三角矩阵，分别代表了某种数据处理的方向。

• 一个向量左乘一个上三角矩阵，得到的结果还是个向量，从形式上看，是着重在对原向量的上半部分进行变化。

• 一个向量左乘一个下三角矩阵，就是在对原向量的下半部分进行各种变化。

-------------------------------

单位矩阵的一个主要用处就是用来寻找inverse，矩阵的逆矩阵。

如果矩阵本身代表一种transform,