Java联立方程组求解

最近遇到解联立方程组的问题，例如已知一个三次多项式函数 ax^3 + bx^2 + cx + d = y 过(1,2)(2,5)(4,3)(6,4)等4个点，求解a b c d。
以前学生时期都是用手算的，现在会编程了，就让程序来代劳吧！

联立方程组解法可参照这篇文章
https://blog.youkuaiyun.com/morrismodel/article/details/100528348

后面直接上代码

import java.util.Arrays;

/**
 * 联立方程组求解
 */
public class SimultaneousEquation {

    private static void printMatrix(double[][] matrix) {
        for (int i = 0 ; i < matrix.length ; i++) {
            System.out.println(Arrays.toString(matrix[i]));
        }
    }

    /**
     * 解联立方程 ax + by = z，已知(x1 y1, z1)、(x2, y2, z2)，求解(a, b)
     * @param matrix [[x1, y1, z1],[x2, y2, z2]]
     * @return [a, b]
     */
    public static double[] solution(double[][] matrix) {
        System.out.println("solution");
        printMatrix(matrix);

        try {
            // 检查矩阵格式， n * n + 1
            int len = matrix.length;
            for (int i = 0 ; i < len ; i++) {
                if(matrix[i].length != len + 1) {
                    System.err.println("matrix[i].length != len + 1");
                    return null;
                }
            }
            // 转阶梯矩阵
            if(!step1(matrix, 0)) {
                System.err.println("!step1");
                return null;
            }
            System.out.println("step1");
            printMatrix(matrix);
            // 转行梯矩阵（前面几项减末行）
            if(!step2(matrix, len - 1)) {
                System.err.println("!step2");
                return null;
            }
            System.out.println("step2");
            printMatrix(matrix);
            // 归一
            for (int i = 0 ; i < len ; i++) {
                double[] mi = matrix[i];
                double v = mi[i];
                multiply(mi, 1 / v);
            }
            System.out.println("step3");
            printMatrix(matrix);
            double[] r = new double[len];
            for (int i = 0 ; i < len ; i++) {
                r[i] = matrix[i][len];
            }
            return r;
        } catch (Exception e){
            e.printStackTrace();
        }
        return null;
    }

    /**
     * 转为倒三角
     * @param matrix
     * @param index
     * @return
     */
    private static boolean step1(double[][] matrix, int index) {
        int ml = matrix.length;

        // 退出条件
        if(index == ml - 1) {
            if(matrix[index][index] == 0) {
                System.err.println("step1 matrix[index][index] == 0");
                return false;
            } else {
                return true;
            }
        }

        // 先检查第一项的首系数不为0，如果第一项首系数为0，需要与后面首系数不为0项互换
        if(matrix[index][index] == 0) {
            for (int i = index; i < ml; i++) {
                if(matrix[i][index] != 0) {
                    swap(matrix, i, index);
                    break;
                } else {
                    if(i == ml - 1) {
                        System.err.println("matrix[j][j] == 0 && j == ml - 1");
                        return false;
                    }
                }
            }
        }

        // 首列
        double[] m0 = matrix[index];
        for (int i = index + 1 ; i < ml ; i++) {
            double[] m1 = matrix[i];
            if(m1[index] == 0) continue;
            multiply(m1, m0[index] / m1[index]); // 被减列通乘 首列首系数/当前列首系数
            minus(m1, m0); // 被减列减增幅首列
        }
        return step1(matrix, index + 1);
    }

    private static boolean step2(double[][] matrix, int index) {
        if(index == 0) {
            if(matrix[index][index] == 0) {
                System.err.println("step2 matrix[index][index] == 0");
                return false;
            } else {
                return true;
            }
        }

        // 末列
        double[] m0 = matrix[index];
        if(m0[index] == 0) {
            System.err.println("m0[index] == 0");
            return false;
        }
        for (int i = 0; i < index; i++) {
            double[] m1 = matrix[i];
            if(m1[index] == 0) continue;
            multiply(m1, m0[index] / m1[index]); // 被减列通乘 末列末系数/当前列末系数
            minus(m1, m0); // 被减列减增幅末列
        }
        return step2(matrix, index - 1);
    }

    private static void swap(double[][] matrix, int i1 ,int i2) {
        double[] tmp = matrix[i1];
        matrix[i1] = matrix[i2];
        matrix[i2] = tmp;
    }

    private static double[] multiply(double[] row, double rate) {
        for (int i = 0 ; i < row.length ; i++) {
            row[i] = row[i] * rate;
        }
        return row;
    }

    private static double[] minus(double[] src, double[] minus) {
        for (int i = 0 ; i < src.length ; i++) {
            src[i] = src[i] - minus[i];
        }
        return src;
    }

    public static void main(String[] args) {
        float [] xs1 = {1, 2, 4, 6};
        float [] ys1 = {2, 5, 3, 4};

        double[][] matrix = new double[xs1.length][];
        for (int i = 0 ; i < xs1.length ; i++) {
            double x = xs1[i];
            double y = ys1[i];
            matrix[i] = new double[]{x * x * x, x * x, x, 1, y};
        }
        double [] r = SimultaneousEquation.solution(matrix);
        if(r == null) {
            System.err.println("r == null");
            return;
        }

        float[] xs2 = new float[60];
        float[] ys2 = new float[60];
        for (int i = 0 ; i < 60 ; i++) {
            double x = 0.5 + i / 10d;
            double y = r[0] * x * x * x + r[1] * x * x + r[2] * x + r[3];
            xs2[i] = (float) x;
            ys2[i] = (float) y;
            System.out.println("x:" + x + ", y:" + y);
        }
    }
}

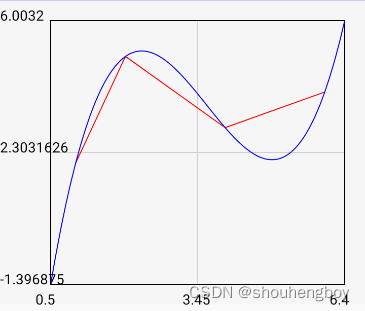
最后上结果图