VAR：视觉生成新范式，投毒风波难掩NeurIPS2024最佳论文！（包含论文代码详解）

1.简介

前几日，字节跳动与前实习生田柯宇之间的纠纷确实引起了广泛的关注。田柯宇在字节跳动实习期间，因涉嫌破坏公司AI训练系统而面临800万元的诉讼。然而，就在这场风波尚未平息之时，田柯宇却因其在视觉生成领域的开创性工作获得了NeurIPS2024最佳论文奖，这无疑为整个事件增添了戏剧性。他的这篇NeurIPS最佳论文，不仅展示了他在学术上的巨大成就，也使得字节跳动错失了一次利用这篇论文进行正面宣传的机会，反而因为诉讼事件而陷入了尴尬的境地。

吃完瓜后，我们再回过头来看看这篇最佳论文。

在当今人工智能领域，图像生成技术正迅速发展，其中自回归模型（AutoRegressive, AR）以其独特的生成方式而备受关注。最近，一项突破性的研究提出了一种名为Visual AutoRegressive（VAR）的新型图像生成范式，它重新定义了图像上的自回归学习，将其视为从粗糙到精细的“next-scale prediction”过程。这项工作不仅在理论上解决了传统AR模型在图像生成中的一些固有问题，而且在实际性能上实现了重大突破，首次使得基于GPT风格的自回归方法在图像合成任务中超越了强大的扩散模型。

VAR模型通过多尺度自回归范式，不仅在ImageNet数据集上取得了显著的性能提升，还在推理速度、数据效率和模型扩展性方面展现了卓越的表现。此外，VAR模型还展现出了零样本任务泛化的能力，这在以往的图像生成模型中是不常见的。这篇文章的深入探讨将带你了解VAR模型的工作原理、技术细节以及它如何为图像生成领域带来革命性的变化。

代码地址：GitHub - FoundationVision/VAR: [NeurIPS 2024 Oral][GPT beats diffusion🔥] [scaling laws in visual generation📈] Official impl. of "Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction". An *ultra-simple, user-friendly yet state-of-the-art* codebase for autoregressive image generation!

权重地址：https://huggingface.co/FoundationVision/var

论文地址：https://arxiv.org/abs/2404.02905
-

2.效果展示

需要注意的是，VAR是刚起步的模型，高质量图像的生成效果和控制相关效果还无法和最先进的生成模型比较（如stable diffusion等），但同规模下的baseline模型比较中，VAR已经超越了如DiT的扩散模型。

3.论文详解

简介

作者提出了Visual AutoRegressive modeling (VAR)，这是一种新一代范式，与标准光栅扫描“next-token预测”不同，它将图像上的自回归学习重新定义为从粗到细的“下一尺度预测”或“下一分辨率预测”。这种简单直观的方法允许自回归（AR）变换器快速学习视觉分布，并且可以很好地泛化：VAR首次使GPT风格的AR模型在图像生成方面超过DiT。除此之外，VAR还延续了LLM的两个重要特性：Scaling Laws and zero-shot泛化。

和以前模型的区别

自回归模型（AR）需要定义数据的顺序。

语言自回归模型：语言本身就有一个固定的顺序，如从左到右，因此我们可以使用自回归模型轻松建模。如GPT、LLaMA等。（图a）反映了顺序语言建模的过程。
之前的视觉自回归模型（图B）：这些模型利用视觉tokenizer将连续图像离散化为2D网格状patch，然后将其展平为用于AR学习的1D序列。然而令人沮丧的是，它们的性能明显落后于扩散模型。
VAR：人类通常以分层的方式感知或创建图像，即首先捕获全局结构，然后捕获局部细节。这种多尺度、从粗到细的性质暗示了图像的“顺序”。作者重新考虑了如何“排序”图像：将图像的自回归学习定义为图（c）中的“下一尺度预测”，与图（B）中的传统“下一标记预测”不同。作者的方法首先将图像编码为多尺度令牌映射。然后，自回归过程从1×1标记图开始，并逐步扩展分辨率：在每一步，VAR以所有以前的token图为条件预测下一个更高分辨率的token图。作者将这种方法称为视觉自回归（VAR）建模。

简单来说，之前的视觉AR是从左到右、从上到下按顺序生成每个patch，然后投入自回归模型学习。这种方式更像早期的照相机（光栅扫描）；而作者提出的VAR模型在生成图像时，先从低分辨率的图像开始，逐步增加分辨率，直到达到目标分辨率。在每个分辨率级别内，模型并行生成整个图像的所有patch，而不是逐行生成（这种方法更像人眼）。

关于怎么转换为不同尺寸的图像，我们下面再说。

方法

自回归模型

自回归模型的数学定义

对于一个离散token序列 $x =(x_1,x_2,...,x_T)$ ，其中xt ∈ [V]是来自大小为V的词表的id。自回归模型假设生成当前token xt的概率仅取决于其前缀 $(x_1,x_2,...,x_{T-1})$ 。这种单向令牌依赖性允许我们能对序列x的似然性进行因式分解： $p(x_1,x_2,...,x_{T}) =\prod_{T}^{t=1}p(x_t|x_1,x_2,...,x_{T-1})$

这被称为“next-token预测”，其训练后的自回归模型pθ可以生成新的序列。

图像自回归模型的离散化

图像本质上是2D连续信号。为了通过下一个标记预测将自回归建模应用于图像，我们必须：将图像转换为若干离散token，并定义用于token的输入顺序。

离散化：我们通常使用量化自动编码器（VQVAE）来将图像特征映射 $f \in R^{h\times w\times C}$ 转换为离散token $q \in \left | V \right |^{h\times w}$ ，VQVAE包括一个可学习codebook $Z \in R^{V\times C}$ ，其包含V个向量。

量化过程q = Q(f)将每个图像的特征向量f(i,j)映射到码本中距离其欧几里德距离最近的编码，然后获取其索引q(i,j)： $q^{(i,j)}=(argmin_{v\in [V]} \left \|lookup(Z,v)-f^{(i,j)} \right \|_2)\in [V]$

其中：

q(i,j)：位置 (i,j) 处的特征向量 f(i,j)量化后得到的codebook索引。
f(i,j)：在位置 (i,j)的原始图像特征向量。
Z：码本（codebook），一个包含 V个向量的集合，每个向量都是图像的一个索引。
lookup(Z,v)：从码本 Z 中查找索引 v 对应的向量。
∥⋅∥2：欧几里得距离（Euclidean distance）的平方，用于计算特征向量与码本向量之间的距离。

公式的核心思想是，对于每个特征向量 f(i,j)，我们在codebook Z 中寻找最接近它的向量，并返回该向量的索引 q(i,j)。这个过程实际上是一个聚类过程，每个特征向量都被分配到最近的聚类中心（即码本向量）。这样的量化方法能够将连续的特征空间离散化，为后续的自回归建模打下基础。

简而言之，公式3定义了如何通过最小化特征向量与码本向量之间的欧几里得距离，将连续的特征向量映射到离散的码本索引。这是VQVAE中关键的一步，它使得模型能够处理离散的图像表示。

损失函数

作者通过codebook Z来查找每个码本索引q(i,j)对应的原向量，然后得到 $\hat{f}$ ，即原始f的近似值。然后，使用给定的解码器D（·）重构新图像 $\hat{im}$ ，并使复合损失L最小化：

$L=\left \| im-\hat{im} \right \|_2+\left \| f-\hat{f} \right \|_2+\lambda _pL_p(\hat{im})+\lambda _GL_G(\hat{im})$

其中各项含义：

L：复合损失函数，用于训练量化自编码器。
$\|im - \hat{im}\|^2$ ：图像重建误差，原始图像 im和重建图像 $\hat{im}$ 之间的均方误差。
$\|f - \hat{f}\|^2$ ：特征重建误差，编码后的特征图 ff 和量化再重建的特征图 $\hat{f}$ 之间的均方误差。
：感知损失，常用于衡量图像重建的视觉质量，例如可以是LPIPS（Learned Perceptual Image Patch Similarity）。见代码详解/训练VAE/损失函数
- LPIPS是一种流行的感知损失，它使用预训练的CNN（如VGG网络）来计算两个图像之间的差异。LPIPS通过比较图像在多个层级的特征表示来衡量它们的相似性，从而提供一个感知上相似度的度量。
：判别损失，常用于图像生成任务中，提升生成图像的真实性，例如可以是StyleGAN的判别器损失。见代码详解/训练VAE/损失函数
- 判别损失（Discriminative Loss）是一类在生成模型中使用的损失函数，特别是在生成对抗网络（GANs）中，它用于指导生成器（Generator）产生更加真实和高质量的输出。判别损失的主要目的是使生成的数据尽可能地接近真实数据，以至于判别器（Discriminator）难以区分生成数据和真实数据。
$\lambda_P$ 和 $\lambda_G$ ：分别对应感知损失和判别损失的权重系数，用于平衡不同损失项对总损失的贡献。

自回归模型的缺点

数学依赖关系的矛盾：在量化自动编码器（VQVAE）中，编码器通常会产生具有双向相关性的信息，这与自回归模型的单向依赖性假设相矛盾。
无法进行某些zero-shot泛化：图像自回归建模的单向性质限制了其在需要双向推理的任务中的泛化能力。例如，在一个示例中，它不能在给定底部的情况下预测图像的顶部。
结构性退化：展平破坏了图像特征图中固有的空间局部性。例如，令牌q（i，j）和它的4个直接相邻者q（i±1，j）、q（i，j±1）由于它们的接近而紧密相关。这种空间关系在线性序列x中受到损害。
效率低下：生成图像令牌序列 $x =(x_1,x_2,...,x_{n\times n})$ 的自回归步长为 $O(n^2)$ ，计算量为 $O(n^6)$

这里我们对论文中提到的效率低下，即 $O(n^6)$ 进行一个证明：

公式17是用于证明在进行自回归（autoregressive）图像生成时的时间复杂度。这个公式计算了在自回归生成过程中，对于一个给定的图像尺寸，需要进行的计算量。以下是公式17的详细解释：

其中：

$n^2$ 表示图像被量化（tokenizer）后的总token数量，如果量化后图像尺寸为 $n \times n$ ，则总token数为 $n^2$ 。
i表示在自回归生成过程中的每一步，需要计算的注意力分数（attention scores）的数量，其中 i从1到 $n^2$ 。
$i^2$ 表示在每一步中，计算所有token之间的注意力分数所需的计算量。

论文公式17的求和计算了从第一个token到最后一个token(一共 $n^2$ 个token)，每一步自注意力计算的总复杂度。具体来说：

对于第一个token，需要计算它与已有的所有token之间的注意力分数，因此复杂度为 $1^2$ 。
对于第二个token，需要计算它与已有的所有token之间的注意力分数，因此复杂度为 $2^2$ 。
以此类推，直到最后一个token(第 $n^2$ 个token)，它需要计算所有的token的注意力分数，因此复杂度为 $(n^2)^2$ 。

将这些复杂度加起来，就得到了整个自回归生成过程的总复杂度。

已知： $1+2+...+n=\frac{1}{6}n(n+1)(2n+1)\sim O(n^3)$

可得： $1+2+...+n^2=\frac{1}{6}n^2(n^2+1)(2n^2+1)\sim O(n^6)$

这个公式表明，对于一个 $n \times n$ 的图像，自回归生成的总计算复杂度是 O( $n^6$ )，这是因为 $n^2$ 个token中每个token都需要与其他 $n^2$ 个token计算注意力分数，从而导致计算量随图像尺寸的增加而呈六次方增长。这种计算复杂度使得传统的自回归模型在处理高分辨率图像时变得非常低效。

VAR

VAR的数学定义

作者通过从“下一个标记预测(next-token)”转变到“下一个尺度预测(next-scale)”的策略来重新定义图像自回归模型。

这里的定义中，每一个token都是对整个图像的映射，而不是单个patch。作者首先将图像特征 $f \in R^{h\times w\times C}$ 量化为K个尺度特征映射（r1，r2，...，rK），每一个r都代表越来越高的分辨率hk × wk(如1×1,2×2...16×16)，在rK时达到目标分辨率。自回归似然性公式表示为： $p(r_1,r_2...,r_K)=\prod_{k=1}^{K}p(r_k|r_1,r_2,...,r_{k-1})$ ，在第k个自回归步骤中序列（r1，r2，...，rk-1）作为rk的“前缀”，并行生成rk中hk ×wk个所有token。

注意，在VAR的训练中，作者使用块式因果注意掩码来确保每个rk只能注意到其前缀r≤k。在推理期间，可以使用kv缓存，并且不需要掩码。

VAR解决了前面提到的三个问题

如果我们限制每个rk只依赖于它的前缀，即得到rk的过程只与r≤k相关，则数学前提是满足的。这种限制是可以接受的，因为它符合自然的、由粗到细的渐进特征，如人类视觉感知和艺术绘画
由于（i）在VAR中不存在展平操作，所以保持了空间局部性。多尺度设计进一步强化了空间结构。
生成具有n×n个潜像的复杂度显著降低到 O( $n^4$ )。该效率增益源自每个rk中的并行令牌生成。

接下来我们对公式22的证明做一个解释：

$k\sum_{i=1}^{k}n^2_i = k\sum_{i=1}^{k}a^{2(i-1)}=\frac{a^{2k}-1}{a^2-1}$ （公式18）

这个公式计算了在VAR模型中，对于前 kk 个尺度级别的所有token的总数。其中：

$n_i$ 表示第 i 个尺度级别的token数量，且 $n_i = a^{i-1}$ 。
a 是一个大于1的常数，表示每个尺度级别token数量的增加比例。
k 是当前考虑的尺度级别数。

第 k个尺度级别的复杂度 = $\left( \frac{a^{2k} - 1}{a^2 - 1} \right)^2$ （公式19）

这个公式计算了在VAR模型中，第 k 个尺度级别的自回归生成的复杂度。这个复杂度是前 k 个尺度级别所有token的总数的平方。

$\sum_{k=1}^{\log_a(n)+1}\left( \frac{a^{2k} - 1}{a^2 - 1} \right)^2$ （公式20）

这个公式计算了在VAR模型中，从第一个尺度级别到最高尺度级别的所有自回归生成的总复杂度。其中：

$\log_a(n)+1$ 表示总共有多少个尺度级别，直到达到最终的图像分辨率 n×n。

总复杂度 = $(a^4-1)\log n + \frac{a^8n^4-2a^6n^2-2a^4(n^2-1)+2a^2-1}{(a^2-1)(a^2+1)}\log a$ (公式21)

这个公式是公式20的简化形式，它将总复杂度表示为一个关于n 和a 的函数。

时间复杂度 of VAR∼ $O(n^4)$ （公式22）

VQVAE

我们开发了一种新的多尺度VQVAE，用于将图像编码为K个多尺度离散token映射 $R =(r_1,r_2,...,r_3,..,r_K)$ 。作者采用了与VQGAN类似的架构，但采用了经过修改的多尺度量化层。算法1和算法2中详细介绍了在f或上进行残差设计的编码和解码过程。作者根据经验发现，这种残差型设计可以比独立插值更好地执行。

对于VQVAE Encoding部分的算法：

初始化空的多尺度令牌列表 R；
对于每个尺度 k 从 1 到 K 执行以下操作：
1. 使用插值将特征图 f 调整到尺度 k 的分辨率 (hk, wk)；
2. 对调整后的图像应用量化器 Q 得到尺度 k 的令牌图 rk；
3. 将 rk 添加到多尺度令牌列表 R；
4. 使用查找表 Z 查找 rk 中每个令牌的向量表示；
5. 将查找得到的向量表示再次插值回最高尺度 hK × wK；
6. 从特征图 f 中减去插值后的向量表示，得到残差，更新 f；
返回多尺度令牌列表 R。

对于VQVAE Reconstruction部分的算法：

初始化重建特征图 ˆf 为0；
对于每个尺度 k 从 1 到 K 执行以下操作：
1. 从多尺度令牌列表 R 中弹出尺度 k 的令牌图 rk；
2. 使用查找表 Z 查找 rk 中每个令牌的向量表示；
3. 将查找得到的向量表示插值回最终尺度 hK × wK；
4. 将插值后的向量表示累加到重建特征图 ˆf；
5. 使用解码器 D 将重建特征图 ˆf 解码成重建图像 ˆim；
6. 返回重建图像 ˆim。

其他细节

VAR tokenizer：作者使用普通VQVAE架构+具有K个额外卷积（0.03M个额外参数）的多尺度量化方案。作者使用词表大小为4096的共享codebook处理所有尺度的信息，另外，空间下采样率为16×。

VAR Transformer：作者采用了类似于GPT-2和VQGAN的decoder-only架构，并采用了自适应归一化（AdaLN）。

对于类条件合成，作者使用类嵌入作为开始标记[s]。

作者没有在大型语言模型中使用高级技术，如旋转位置嵌入（RoPE）、SwiGLU MLP或RMS Norm。

作者的模型形状遵循简单尺寸规则，即宽度w、头数h和跌落率dr与深度d成线性比例，如下所示： $w = 64d, h = d, dr = 0.1 · d/24.$

因此，具有深度d的VAR Transformer的主要参数量N可由下式得出：

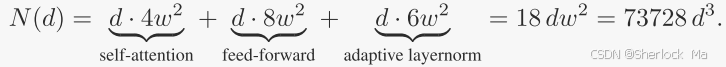
其中：

4：自注意力（self-attention）模块的参数数量。在Transformer模型中，自注意力模块通常包含查询（query）、键（key）、值（value）和输出投影（output projection）四个线性变换。每个变换的参数数量是 $w^2$ （因为它们是 $w \times w$ 的矩阵），所以自注意力模块的总参数数量是 $4w^2$ 。
8：前馈网络（feed-forward network）的参数数量。在Transformer模型中，前馈网络通常包含两个线性变换，中间有一个激活函数。如果中间层的维度是 ww 的两倍，那么前馈网络的参数数量是 $2w \times w + w \times 2w = 4w^2$ 。但是，由于前馈网络通常包含两个这样的层（一个用于增加维度，一个用于减少维度），所以总参数数量是 $2 \times 4w^2 = 8w^2$ 。
6：自适应层归一化（adaptive layernorm）的参数数量。在Transformer模型中，每个层通常包含一个层归一化（layernorm）模块，它有两个参数：一个用于缩放（scale），一个用于偏移（shift）。由于每个层都有3个自适应层归一化模块，所以总参数数量是 $6w^2$ 。

限制

文本提示生成：由于VAR的模型结构与大语言模型基本相似，因此可以很容易地与大语言模型兼容，以实现文本到图像的生成，但这篇文章没有做。

视频生成：在本作品中没有实现视频生成，但可以自然扩展。通过将多尺度视频特征视为3D金字塔，可以制定类似的“3D下一尺度预测”以通过VAR生成视频。

与基于扩散的生成器（如sora）相比，VAR方法在时间一致性或与LLM集成方面具有固有优势，因此可以处理更长的时间依赖性。传统的AR模型由于其极高的计算复杂度和缓慢的推理速度，使得使用传统AR模型生成高分辨率视频变得昂贵得令人望而却步，而VAR能够解决这一问题。

4.代码详解

环境搭建

安装 torch>=2.0.0。
通过 pip3 install -r requirements.txt 安装其他 pip 软件包。
准备 ImageNet 数据集（如果只推理，不训练不需要这步）
(可选）安装并编译 flash-attn 和 xformers 以加快注意力计算。如果已安装，代码将自动使用它们。参见 models/basic_var.py#L15-L30。

下载模型权重：https://huggingface.co/FoundationVision/var/tree/main

（注意：我们只需要下载vae和其中1个var即可，var可根据自己电脑配置选择）

model	reso.	FID	rel. cost	#params	HF weights🤗
VAR-d16	256	3.55	0.4	310M	var_d16.pth
VAR-d20	256	2.95	0.5	600M	var_d20.pth
VAR-d24	256	2.33	0.6	1.0B	var_d24.pth
VAR-d30	256	1.97	1	2.0B	var_d30.pth
VAR-d30-re	256	1.80	1	2.0B	var_d30.pth

在demo_sample.ipynb里修改参数：

MODEL_DEPTH：设置模型深度，之前下载的VAR权重后面有d16、d30，这里的数字就是权重文件后面的d，默认16
- 需要注意的是，如果你下载的是12的权重，要把assert MODEL_DEPTH in {16, 20, 24, 30}改成assert MODEL_DEPTH in {12, 16, 20, 24, 30}
vae_ckpt, var_ckpt：注意权重路径

使用

参数设置：

num_sampling_steps：采样步长，从1到1000
cfg = 10：classifier-free guidance ratio
class_labels：要生成的图像序号，是ImageNet中的类别序号，从0到1000
more_smooth：True代表更平滑的输出

删除随机数种子：

作者设置了固定随机数种子的步骤，因此每次生成的图片是一样的，如果想生成不一样的图片，请把下面的代码注释掉：

# seed  固定随机数种子
torch.manual_seed(seed)
random.seed(seed)
np.random.seed(seed)
torch.backends.cudnn.deterministic = True       # 设置CUDNN确定性，确保每次运行的结果是确定性的，这对于调试和复现实验结果非常重要
torch.backends.cudnn.benchmark = False          # 禁用CUDNN的自动优化功能，避免在每次运行时选择不同的算法导致结果不一致。

并删除以下代码里面的参数g_seed

recon_B3HW = var.autoregressive_infer_cfg(B=B, label_B=label_B, cfg=cfg, top_k=900, top_p=0.95, more_smooth=more_smooth)       # [b,3,256,256]

在demo_sample.ipynb里设置完想要的参数后，直接运行即可。

下面是对其代码的解释：

import os
import os.path as osp
import torch, torchvision
import random
import numpy as np
import PIL.Image as PImage, PIL.ImageDraw as PImageDraw
setattr(torch.nn.Linear, 'reset_parameters', lambda self: None)     # disable default parameter init for faster speed
setattr(torch.nn.LayerNorm, 'reset_parameters', lambda self: None)  # disable default parameter init for faster speed
from models import VQVAE, build_vae_var


MODEL_DEPTH = 30    # 设置模型深度，作者提供了12-30的多个版本
ckpt_dir = "FoundationVision/var/"      # 权重路径
assert MODEL_DEPTH in {16, 20, 24, 30}

# download checkpoint       # 没下载，就从huggingface下载
hf_home = 'https://huggingface.co/FoundationVision/var/resolve/main'
vae_ckpt, var_ckpt = ckpt_dir+'vae_ch160v4096z32.pth', ckpt_dir+f'var_d{MODEL_DEPTH}.pth'   # 拼接权重路径
if not osp.exists(vae_ckpt): os.system(f'wget {hf_home}/{vae_ckpt}')
if not osp.exists(var_ckpt): os.system(f'wget {hf_home}/{var_ckpt}')


# build vae, var    创建vae和var模型
patch_nums = (1, 2, 3, 4, 5, 6, 8, 10, 13, 16)      # patch尺寸
device = 'cuda' if torch.cuda.is_available() else 'cpu'
if 'vae' not in globals() or 'var' not in globals():
    vae, var = build_vae_var(
        V=4096, Cvae=32, ch=160, share_quant_resi=4,    # hard-coded VQVAE hyperparameters
        device=device, patch_nums=patch_nums,
        num_classes=1000, depth=MODEL_DEPTH, shared_aln=False,
    )

# load checkpoints  加载权重并冻结参数
vae.load_state_dict(torch.load(vae_ckpt, map_location='cpu'), strict=True)
var.load_state_dict(torch.load(var_ckpt, map_location='cpu'), strict=True)
vae.eval(), var.eval()
for p in vae.parameters(): p.requires_grad_(False)
for p in var.parameters(): p.requires_grad_(False)
print(f'prepare finished.')


############################# 2. Sample with classifier-free guidance
# set args
seed = 0            # @param {type:"number"}
num_sampling_steps = 250    # @param {type:"slider", min:0, max:1000, step:1}
cfg = 10                    # @param {type:"slider", min:1, max:10, step:0.1}
class_labels = (58, 18)   # ImageNet中的类别序号，最大1000 @param {type:"raw"}
more_smooth = True # True for more smooth output

# seed  固定随机数种子
torch.manual_seed(seed)
random.seed(seed)
np.random.seed(seed)
torch.backends.cudnn.deterministic = True       # 设置CUDNN确定性，确保每次运行的结果是确定性的，这对于调试和复现实验结果非常重要
torch.backends.cudnn.benchmark = False          # 禁用CUDNN的自动优化功能，避免在每次运行时选择不同的算法导致结果不一致。

# run faster
tf32 = True
torch.backends.cudnn.allow_tf32 = bool(tf32)    # 设置CuDNN库是否允许使用TF32精度进行卷积运算。
torch.backends.cuda.matmul.allow_tf32 = bool(tf32)  # 设置CUDA矩阵乘法是否允许使用TF32精度。
torch.set_float32_matmul_precision('high' if tf32 else 'highest')   # 根据 tf32 的值，设置浮点数矩阵乘法的精度为 high 或 highest。

# sample 生成图片
B = len(class_labels)       # 要生成的图片的数量
label_B: torch.LongTensor = torch.tensor(class_labels, device=device)
with torch.inference_mode():
    with torch.autocast('cuda', enabled=True, dtype=torch.float16, cache_enabled=True):    # using bfloat16 can be faster
        recon_B3HW = var.autoregressive_infer_cfg(B=B, label_B=label_B, cfg=cfg, top_k=900, top_p=0.95, g_seed=seed, more_smooth=more_smooth)

# 绘图
chw = torchvision.utils.make_grid(recon_B3HW, nrow=8, padding=0, pad_value=1.0)
chw = chw.permute(1, 2, 0).mul_(255).cpu().numpy()
chw = PImage.fromarray(chw.astype(np.uint8))
chw.show()

build_vae_var()

vae, var = build_vae_var(
    V=4096, Cvae=32, ch=160, share_quant_resi=4,    # hard-coded VQVAE hyperparameters
    device=device, patch_nums=patch_nums,
    num_classes=1000, depth=MODEL_DEPTH, shared_aln=False,
)

具体实现如下：

def build_vae_var(...) -> Tuple[VQVAE, VAR]:
    # 论文中公式7提到的h、w、dpr
    heads = depth
    width = depth * 64
    dpr = 0.1 * depth/24
    
    # disable built-in initialization for speed     禁用PyTorch中一些常用层类的参数初始化功能,用于加速
    for clz in (nn.Linear, nn.LayerNorm, nn.BatchNorm2d, nn.SyncBatchNorm, nn.Conv1d, nn.Conv2d, nn.ConvTranspose1d, nn.ConvTranspose2d):
        setattr(clz, 'reset_parameters', lambda self: None)     # 将reset_parameters方法重写为一个空的lambda函数，即lambda self: None。这样做的目的是在创建这些层时，不执行默认的参数初始化，从而加快模型构建的速度。
    
    # build models    创建模型
    vae_local = VQVAE(vocab_size=V, z_channels=Cvae, ch=ch, test_mode=True, share_quant_resi=share_quant_resi, v_patch_nums=patch_nums).to(device)
    var_wo_ddp = VAR(
        vae_local=vae_local,
        num_classes=num_classes, depth=depth, embed_dim=width, num_heads=heads, drop_rate=0., attn_drop_rate=0., drop_path_rate=dpr,
        norm_eps=1e-6, shared_aln=shared_aln, cond_drop_rate=0.1,
        attn_l2_norm=attn_l2_norm,
        patch_nums=patch_nums,
        flash_if_available=flash_if_available, fused_if_available=fused_if_available,
    ).to(device)
    # 初始化var
    var_wo_ddp.init_weights(init_adaln=init_adaln, init_adaln_gamma=init_adaln_gamma, init_head=init_head, init_std=init_std)

    return vae_local, var_wo_ddp

其中，前几行的head、width、dpr就是论文中公式7： $w = 64d, h = d, dr = 0.1 · d/24.$

# 论文中公式7提到的h、w、dpr
heads = depth
width = depth * 64
dpr = 0.1 * depth/24

接着，作者禁用了torch库中一些层的初始化方法，用于加快初始化速度。

具体来说：

遍历层类：代码遍历了这些常用的层类。
重写reset_parameters方法：对于每个层类，将reset_parameters方法重写为一个空的lambda函数，即lambda self: None。这样做的目的是在创建这些层时，不执行默认的参数初始化，从而加快模型构建的速度。

# disable built-in initialization for speed     禁用PyTorch中一些常用层类的参数初始化功能,用于加速
for clz in (nn.Linear, nn.LayerNorm, nn.BatchNorm2d, nn.SyncBatchNorm, nn.Conv1d, nn.Conv2d, nn.ConvTranspose1d, nn.ConvTranspose2d):
    setattr(clz, 'reset_parameters', lambda sel

然后是模型的定义与var的初始化

线性层：使用trunc_normal_初始化权重，标准差为 init_std，如果有偏置则将其初始化为0。
嵌入层：使用trunc_normal_初始化权重，标准差为 init_std，如果有填充索引则将其初始化为0。
归一化层：如果模块有权重则将其初始化为1，如果有偏置则将其初始化为0。
卷积层：根据 conv_std_or_gain 的值选择不同的初始化方法（包括trunc_normal_、xavier_normal_），如果有偏置则将其初始化为0。
头部层初始化：如果 init_head 大于等于0，对头部层进行初始化：
- 线性层：将权重乘以 init_head，并将偏置初始化为0。
- 序列层：将最后一个线性层的权重乘以 init_head，并将偏置初始化为0。
自适应层初始化：如果头部层的归一化模块是 AdaLNBeforeHead 类型
- 将 ada_lin 的权重乘以 init_adaln 和 init_adaln_gamma，如果有偏置则将其初始化为0。
块层初始化：遍历所有块层，对每个块中的注意力机制和前馈网络进行初始化：
- 注意力机制：将投影层的权重除以 sqrt(2 * depth)。
- 前馈网络：将第二层全连接层的权重除以 sqrt(2 * depth)，如果有 fcg 则初始化其权重和偏置。
- 自适应层：根据 ada_lin 或 ada_gss 的存在与否进行相应的初始化。

autoregressive_infer_cfg

with torch.inference_mode():
    with torch.autocast('cuda', enabled=True, dtype=torch.float16, cache_enabled=True):    # using bfloat16 can be faster
        recon_B3HW = var.autoregressive_infer_cfg(B=B, label_B=label_B, cfg=cfg, top_k=900, top_p=0.95, g_seed=seed, more_smooth=more_smooth)

进入models/var.py下的VAR类的autoregressive_infer_cfg()函数

首先是初始化随机数生成器rng，如果没有设置g_seed，则rng=None，否则设置rng=torch.Generator

## 1. 初始化随机数生成器
if g_seed is None: rng = None       # 初始化随机数生成器
else: self.rng.manual_seed(g_seed); rng = self.rng      # rng是torch.Generator()

## 2. 处理标签
if label_B is None:     # 如果 label_B 为 None，则随机生成标签。
    label_B = torch.multinomial(self.uniform_prob, num_samples=B, replacement=True, generator=rng).reshape(B)
elif isinstance(label_B, int):      # 如果label_B是int类型，则根据传入的标签值创建标签张量。
    label_B = torch.full((B,), fill_value=self.num_classes if label_B < 0 else label_B, device=self.lvl_1L.device)  # 如果 label_B 小于 0，则填充值为 self.num_classes
# 默认传入是列表，因此上面两个都不走

初始化输入

生成初始状态 sos：使用 class_emb 将标签 label_B 和填充值 num_classes 组合成一个新的张量，并通过嵌入层转换为特征向量 sos。
生成位置编码 lvl_pos：通过 lvl_embed 和 pos_1LC 生成位置编码 lvl_pos。
构建下一个 token 的映射 next_token_map：将 sos 扩展并加上起始位置编码 pos_start 和部分 lvl_pos，生成 next_token_map。

## 3. 生成初始状态 sos 和位置编码 lvl_pos
sos = cond_BD = self.class_emb(torch.cat((label_B, torch.full_like(label_B, fill_value=self.num_classes)), dim=0))      # [2b]->[2b,1920]
lvl_pos = self.lvl_embed(self.lvl_1L) + self.pos_1LC        # [1,680,1920]
next_token_map = sos.unsqueeze(1).expand(2 * B, self.first_l, -1) + self.pos_start.expand(2 * B, self.first_l, -1) + lvl_pos[:, :self.first_l]      # [2b,1,1920]

由于作者的代码中充斥着简写，因此我下面把这些代码展开解读，详细解读如下：

第一行代码实际上就是将无条件控制的信息和有条件控制的信息拼接起来，然后经过一个embedding层进行嵌入，获得一个维度为1920的向量。

t1 = torch.cat((label_B, torch.full_like(label_B, fill_value=self.num_classes)), dim=0)     # [2b],列如输入是[58,477]，输出就是[58,477,1000,1000]，后面两个是无条件的标签
sos = cond_BD = self.class_emb(t1)  # 将条件控制信息和无条件控制信息嵌入向量 [2b]->[2b,1920]

其中，t1的值和sos向量的尺寸如下：

t1的值： [  58,   18, 1000, 1000]
sos的长度：[4,1920]

第二行代码接着生成位置编码，首先通过embedding将lvl_1L嵌入成[1,680,1920]的向量，然后和可学习的位置编码pos_1LC相加

l1 = self.lvl_embed(self.lvl_1L)    # 将位置编码嵌入向量 [1,680,1920]
lvl_pos = l1 + self.pos_1LC         # 加入可学习的位置编码[1,680,1920]

其中lvl_1L的值如下（1个0,4个1,9个2,16个3...，数量随着尺寸大小逐渐放大，总计680个）：

tensor([[0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
         3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, ...    9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9,
         9, 9, 9, 9, 9, 9, 9, 9]], device='cuda:0')

第三行代码实际上是将sos转换为适当的长度，然后和位置编码起始位置pos_start、位置编码lvl_pos相加

next_token_map = sos.unsqueeze(1)   # [2b,1920]->[2b,1,1920]
next_token_map = next_token_map.expand(2 * B, self.first_l, -1)     # [2b,1,1920]->[2b,1,1920]
next_token_map = next_token_map + self.pos_start.expand(2 * B, self.first_l,-1) + lvl_pos[:,:self.first_l]  # [2b,1,1920]

循环生成每个片段

完整代码：

## 4. 循环生成每个片段
cur_L = 0       # 对于每个片段，计算当前片段的位置索引 cur_L
f_hat = sos.new_zeros(B, self.Cvae, self.patch_nums[-1], self.patch_nums[-1])   # 初始化最终输出张量，尺寸全程不变 [b,Cvae,patch_nums[-1],patch_nums[-1]]=[2,32,16,16]

for b in self.blocks: b.attn.kv_caching(True)   # 启用缓存
for si, pn in enumerate(self.patch_nums):   # si: i-th segment  pn:patch块的尺寸  patch_nums:(1, 2, 3, 4, 5, 6, 8, 10, 13, 16)
    # 4.1 参数更新
    ratio = si / self.num_stages_minus_1
    # last_L = cur_L
    cur_L += pn*pn      # 计算当前片段的长度 cur_L。
    # assert self.attn_bias_for_masking[:, :, last_L:cur_L, :cur_L].sum() == 0, f'AR with {(self.attn_bias_for_masking[:, :, last_L:cur_L, :cur_L] != 0).sum()} / {self.attn_bias_for_masking[:, :, last_L:cur_L, :cur_L].numel()} mask item'
    cond_BD_or_gss = self.shared_ada_lin(cond_BD)       # 默认Identity()，即一个不进行任何操作的层。
    x = next_token_map      # 输入

    # 4.2 计算
    AdaLNSelfAttn.forward
    for b in self.blocks:
        x = b(x=x, cond_BD=cond_BD_or_gss, attn_bias=None)      # [2b,pn^2,1920]
    logits_BlV = self.get_logits(x, cond_BD)    # adaLN [2b,pn^2,4096]
    
    t = cfg * ratio
    logits_BlV = (1+t) * logits_BlV[:B] - t * logits_BlV[B:]        # classifer-free guidance

    # 4.3 平滑处理
    idx_Bl = sample_with_top_k_top_p_(logits_BlV, rng=rng, top_k=top_k, top_p=top_p, num_samples=1)[:, :, 0]    # 默认后续代码不需要这个，转换为令牌id [b,pn]
    if not more_smooth: # this is the default case  平滑处理
        h_BChw = self.vae_quant_proxy[0].embedding(idx_Bl)   # B, l, Cvae
    else:   # not used when evaluating FID/IS/Precision/Recall
        gum_t = max(0.27 * (1 - ratio * 0.95), 0.005)   # refer to mask-git
        h_BChw = gumbel_softmax_with_rng(logits_BlV.mul(1 + ratio), tau=gum_t, hard=False, dim=-1, rng=rng) @ self.vae_quant_proxy[0].embedding.weight.unsqueeze(0)     # [b,pn^2,Cvae]

    # 4.4 插值运算
    h_BChw = h_BChw.transpose_(1, 2).reshape(B, self.Cvae, pn, pn)      # [b,Cvae,pn,pn]=[2,32,pn,pn]
    f_hat, next_token_map = self.vae_quant_proxy[0].get_next_autoregressive_input(si, len(self.patch_nums), f_hat, h_BChw)  # 更新    # [b,Cvae,pn+1,pn+1]=[2,32,pn+1,pn+1] pn+1是下一层的尺寸

    # 4.5 更新参数，为下一阶段做准备
    if si != self.num_stages_minus_1:   # 如果不是最后阶段，为下一阶段做准备 prepare for next stage    更新输入
        next_token_map = next_token_map.view(B, self.Cvae, -1).transpose(1, 2)          # [b,pn^2,Cvae]=[b,pn^2,32]
        next_token_map = self.word_embed(next_token_map) + lvl_pos[:, cur_L:cur_L + self.patch_nums[si+1] ** 2]     # [b,pn^2,Cvae]->[b,pn^2,1920],并加入位置编码
        next_token_map = next_token_map.repeat(2, 1, 1)   # double the batch sizes due to CFG   # [2b,pn^2,1920]

初始化

初始化的主要步骤如下：

初始化当前片段长度 cur_L和输出张量 f_hat。
1. 当前片段长度 cur_L ：用于后续加入位置信息时计算位置)
2. 输出张量 f_hat：每次循环的输出实际上就是在不断更新这个，他的尺寸不会变，最终输出时会经过VQVAE转换为图片
遍历每个块 b，启用缓存机制。

## 4. 循环生成每个片段
cur_L = 0       # 对于每个片段，计算当前片段的长度 cur_L
f_hat = sos.new_zeros(B, self.Cvae, self.patch_nums[-1], self.patch_nums[-1])   # 最终输出张量，尺寸不变 [b,Cvae,patch_nums[-1],patch_nums[-1]]=[2,32,16,16]


for b in self.blocks: b.attn.kv_caching(True)   # 启用缓存

AdaLNSelfAttn

# 4.2 计算
AdaLNSelfAttn.forward
for b in self.blocks:
    x = b(x=x, cond_BD=cond_BD_or_gss, attn_bias=None)      # [2b,pn^2,1920]
logits_BlV = self.get_logits(x, cond_BD)    # adaLN [2b,pn^2,4096]

AdaLNSelfAttn定义如下：

我们可以看到，这个类和DiT一样都设置了gamma、scale&shift，关于Transformer相关的问题就不多介绍了。除此之外这里还使用了drop_path(仅训练时有效），用于在训练过程中随机丢弃（即设置为零）网络中的某些层来防止过拟合，并促进模型的泛化能力。

class AdaLNSelfAttn(nn.Module):
    def __init__(...):
        ...
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()   # 通过在训练过程中随机丢弃（即设置为零）网络中的某些层来防止过拟合，并促进模型的泛化能力。
        self.attn = SelfAttention(block_idx=block_idx, embed_dim=embed_dim, num_heads=num_heads, attn_drop=attn_drop, proj_drop=drop, attn_l2_norm=attn_l2_norm, flash_if_available=flash_if_available)
        self.ffn = FFN(in_features=embed_dim, hidden_features=round(embed_dim * mlp_ratio), drop=drop, fused_if_available=fused_if_available)
        
        self.ln_wo_grad = norm_layer(embed_dim, elementwise_affine=False)
        self.shared_aln = shared_aln
        if self.shared_aln:
            self.ada_gss = nn.Parameter(torch.randn(1, 1, 6, embed_dim) / embed_dim**0.5)
        else:
            lin = nn.Linear(cond_dim, 6*embed_dim)
            self.ada_lin = nn.Sequential(nn.SiLU(inplace=False), lin)
        
        self.fused_add_norm_fn = None
    
    # NOTE: attn_bias is None during inference because kv cache is enabled
    def forward(self, x, cond_BD, attn_bias):   # C: embed_dim, D: cond_dim
        if self.shared_aln:
            gamma1, gamma2, scale1, scale2, shift1, shift2 = (self.ada_gss + cond_BD).unbind(2) # 116C + B16C =unbind(2)=> 6 B1C
        else:
            gamma1, gamma2, scale1, scale2, shift1, shift2 = self.ada_lin(cond_BD).view(-1, 1, 6, self.C).unbind(2)
        x = x + self.drop_path(self.attn( self.ln_wo_grad(x).mul(scale1.add(1)).add_(shift1), attn_bias=attn_bias ).mul_(gamma1))
        x = x + self.drop_path(self.ffn( self.ln_wo_grad(x).mul(scale2.add(1)).add_(shift2) ).mul(gamma2)) # this mul(gamma2) cannot be in-placed when FusedMLP is used
        return x

接着进行归一化和线性层转化

def get_logits(self, h_or_h_and_residual: Union[torch.Tensor, Tuple[torch.Tensor, torch.Tensor]], cond_BD: Optional[torch.Tensor]):
    if not isinstance(h_or_h_and_residual, torch.Tensor):
        h, resi = h_or_h_and_residual   # fused_add_norm must be used
        h = resi + self.blocks[-1].drop_path(h)
    else:                               # fused_add_norm is not used
        h = h_or_h_and_residual     # 默认走这里
    return self.head(self.head_nm(h.float(), cond_BD).float()).float()      # adaLN

其中head_nm是层归一化AdaLN,head是线性层，将1920维向量转换为4096维向量。

self.head_nm = AdaLNBeforeHead(self.C, self.D, norm_layer=norm_layer)
self.head = nn.Linear(self.C, self.V)

接着是生成任务中常见的分类器自由引导（Classifier-Free Guidance）技术，它是一种在生成模型中用于提高生成质量的方法。

t = cfg * ratio
logits_BlV = (1+t) * logits_BlV[:B] - t * logits_BlV[B:]        # classifer-free guidance

分类器自由引导的目的是通过调整条件和无条件信息的相对权重来提高生成质量。具体来说，它通过增加条件信息的权重并减少无条件信息的权重，使生成过程更加依赖于给定的条件，从而生成更加逼真和符合条件的图像。

平滑处理

# 4.3 平滑处理
idx_Bl = sample_with_top_k_top_p_(logits_BlV, rng=rng, top_k=top_k, top_p=top_p, num_samples=1)[:, :, 0]    # 默认后续代码不需要这个，转换为令牌id [b,pn]
if not more_smooth: # this is the default case  平滑处理
    h_BChw = self.vae_quant_proxy[0].embedding(idx_Bl)   # B, l, Cvae
else:   # not used when evaluating FID/IS/Precision/Recall
    gum_t = max(0.27 * (1 - ratio * 0.95), 0.005)   # refer to mask-git
    h_BChw = gumbel_softmax_with_rng(logits_BlV.mul(1 + ratio), tau=gum_t, hard=False, dim=-1, rng=rng) @ self.vae_quant_proxy[0].embedding.weight.unsqueeze(0)     # [b,pn^2,Cvae]

其中，sample_with_top_k_top_p_()的目的是转换为离散令牌id，但是实际上默认情况下后续没有用到其结果idx_Bl

def sample_with_top_k_top_p_(logits_BlV: torch.Tensor, top_k: int = 0, top_p: float = 0.0, rng=None, num_samples=1) -> torch.Tensor:  # return idx, shaped (B, l)
    B, l, V = logits_BlV.shape
    if top_k > 0:   # 如果 top_k 大于 0，移除不在前 k 个最高 logits 之外的所有 logits。
        idx_to_remove = logits_BlV < logits_BlV.topk(top_k, largest=True, sorted=False, dim=-1)[0].amin(dim=-1, keepdim=True)
        logits_BlV.masked_fill_(idx_to_remove, -torch.inf)
    if top_p > 0:       # 如果 top_p 大于 0，移除累积概率小于 1 - p 的所有 logits。
        sorted_logits, sorted_idx = logits_BlV.sort(dim=-1, descending=False)
        sorted_idx_to_remove = sorted_logits.softmax(dim=-1).cumsum_(dim=-1) <= (1 - top_p)
        sorted_idx_to_remove[..., -1:] = False
        logits_BlV.masked_fill_(sorted_idx_to_remove.scatter(sorted_idx.ndim - 1, sorted_idx, sorted_idx_to_remove), -torch.inf)
    # sample (have to squeeze cuz torch.multinomial can only be used for 2D tensor)
    replacement = num_samples >= 0
    num_samples = abs(num_samples)
    # 使用 torch.multinomial 从处理后的 logits 中进行采样，返回形状为 (B, l, num_samples) 的张量。
    return torch.multinomial(logits_BlV.softmax(dim=-1).view(-1, V), num_samples=num_samples, replacement=replacement, generator=rng).view(B, l, num_samples)

而gumbel_softmax_with_rng()默认会走F.gumbel_softmax()

def gumbel_softmax_with_rng(logits: torch.Tensor, tau: float = 1, hard: bool = False, eps: float = 1e-10, dim: int = -1, rng: torch.Generator = None) -> torch.Tensor:
    if rng is None:
        return F.gumbel_softmax(logits=logits, tau=tau, hard=hard, eps=eps, dim=dim)

Gumbel-Softmax函数的工作原理是，首先在logits上添加Gumbel噪声，然后应用Softmax函数。这样可以使得在训练过程中，模型可以学习到离散变量的分布，同时保持梯度的连续性，从而可以使用标准的反向传播算法进行训练。

在生成模型中，Gumbel-Softmax函数常用于生成离散变量，如在变分自编码器（VAE）中生成离散的隐变量，或者在序列生成模型中生成离散的输出。通过调整温度参数 tau，可以控制生成的离散变量的确定性或随机性。

插值放大

# 4.4 插值运算
h_BChw = h_BChw.transpose_(1, 2).reshape(B, self.Cvae, pn, pn)      # [b,Cvae,pn,pn]=[2,32,pn,pn]
f_hat, next_token_map = self.vae_quant_proxy[0].get_next_autoregressive_input(si, len(self.patch_nums), f_hat, h_BChw)  # 更新    # [b,Cvae,pn+1,pn+1]=[2,32,pn+1,pn+1] pn+1是下一层的尺寸

其中get_next_autoregressive_input()的过程如下：

对于如果 si 不等于 SN-1：

对输入张量 h_BChw 进行双三次插值放大到目标尺寸 (HW, HW)，获得t。
将插值后的张量通过 quant_resi 层进行处理，获得h。
将处理结果原地加到 f_hat 上。
返回 f_hat 和 f_hat 经过插值缩小后的结果（这次缩小不会回到最开始的尺寸，而是缩小到下一级的尺寸）。

我们以h_BChw=[b,32,1,1]为例，t=[b,32,16,16]，h=[b,32,16,16]，f_hat=[b,32,16,16]，最终返回的第二个返回值尺寸是[b,32,2,2]

class VectorQuantizer2(nn.Module):
    def get_next_autoregressive_input(self, si: int, SN: int, f_hat: torch.Tensor, h_BChw: torch.Tensor) -> Tuple[Optional[torch.Tensor], torch.Tensor]: # only used in VAR inference
        HW = self.v_patch_nums[-1]      # 要生成的目标尺寸，16
        if si != SN-1:      # 如果当前索引 si 不等于总步数 SN-1
            # h = self.quant_resi[si/(SN-1)](F.interpolate(h_BChw, size=(HW, HW), mode='bicubic'))     # 插值放大 conv after upsample
            t = F.interpolate(h_BChw, size=(HW, HW), mode='bicubic')    # 对输入张量 h_BChw 进行双三次插值放大到目标尺寸 (HW, HW)。
            h = self.quant_resi[si / (SN - 1)](t)
            f_hat.add_(h)       # 原地运算
            return f_hat, F.interpolate(f_hat, size=(self.v_patch_nums[si+1], self.v_patch_nums[si+1]), mode='area')    # 插值缩小到下一层的尺寸
        else:
            h = self.quant_resi[si/(SN-1)](h_BChw)
            f_hat.add_(h)
            return f_hat, f_hat

其中self.quant_resi的定义，如下：

class PhiPartiallyShared(nn.Module):
    def __init__(self, qresi_ls: nn.ModuleList):
        super().__init__()
        self.qresi_ls = qresi_ls
        K = len(qresi_ls)
        self.ticks = np.linspace(1/3/K, 1-1/3/K, K) if K == 4 else np.linspace(1/2/K, 1-1/2/K, K)
    
    def __getitem__(self, at_from_0_to_1: float) -> Phi:
        # 1.计算self.ticks数组中每个元素与at_from_0_to_1的绝对差值。
        # 2.找到最小差值的索引：使用np.argmin找到上述差值数组中最小值的索引。
        # 3.返回对应的Phi对象：根据找到的索引从self.qresi_ls列表中返回对应的Phi对象。
        return self.qresi_ls[np.argmin(np.abs(self.ticks - at_from_0_to_1)).item()]

我们在调用self.quant_resi[si / (SN - 1)]时，实际上是调用其中的__getitem__()方法，具体来说，这里计算self.ticks数组中每个元素与si / (SN - 1)的绝对差值，选最小的，然后调用self.qresi_ls里面对应的Phi卷积。

self.ticks数组的元素如下：

[0.08333333 0.36111111 0.63888889 0.91666667]

而Phi的定义如下，简单来说是作者定义的一个卷积层

首先，计算 h_BChw 乘以 (1 - self.resi_ratio)。
然后，调用父类 nn.Conv2d 的 forward 方法对 h_BChw 进行卷积操作，并将结果乘以 self.resi_ratio。
最后，将上述两个结果相加并返回。

这种实现方式的目的是为了在卷积操作中引入量化残差（quantization residual）。具体来说，self.resi_ratio 控制量化残差的比例，允许模型在卷积操作中保留一部分量化误差，这可以增加模型对量化噪声的鲁棒性，使得模型在训练过程中学习如何平衡原始特征和量化误差的影响，这种方法可能用于提高模型在量化环境下的性能。

class Phi(nn.Conv2d):   # 继承卷积
    def __init__(self, embed_dim, quant_resi):
        ks = 3
        super().__init__(in_channels=embed_dim, out_channels=embed_dim, kernel_size=ks, stride=1, padding=ks//2)
        self.resi_ratio = abs(quant_resi)
    
    def forward(self, h_BChw):
        # 1.计算 h_BChw 乘以 (1 - self.resi_ratio)。
        # 2.调用父类 nn.Conv2d 的 forward 方法对 h_BChw 进行卷积操作，并将结果乘以 self.resi_ratio。
        # 3. 将上述两个结果相加并返回。
        return h_BChw.mul(1-self.resi_ratio) + super().forward(h_BChw).mul_(self.resi_ratio)

更新参数

更新next_token_map，为下一次循环做准备。

# 4.5 更新参数，为下一阶段做准备
if si != self.num_stages_minus_1:   # 如果不是最后阶段，为下一阶段做准备 prepare for next stage    更新输入
    next_token_map = next_token_map.view(B, self.Cvae, -1).transpose(1, 2)          # [b,pn^2,Cvae]=[b,pn^2,32]
    next_token_map = self.word_embed(next_token_map) + lvl_pos[:, cur_L:cur_L + self.patch_nums[si+1] ** 2]     # [b,pn^2,Cvae]->[b,pn^2,1920],并加入位置编码
    next_token_map = next_token_map.repeat(2, 1, 1)   # double the batch sizes due to CFG   # [2b,pn^2,1920]

输出

这里进行反归一化并使用VQVAE的decoder进行解码

for b in self.blocks: b.attn.kv_caching(False)
return self.vae_proxy[0].fhat_to_img(f_hat).add_(1).mul_(0.5)   # de-normalize, from [-1, 1] to [0, 1]

其中self.vae_proxy[0]是VQVAE，其方法fhat_to_img如下：

post_quant_conv：首先通过 self.post_quant_conv 对 f_hat 进行卷积操作。
decoder：然后将卷积后的结果传递给解码器 self.decoder 进行解码。
clamp：最后对解码后的结果进行裁剪，确保所有像素值在 -1 到 1 之间。

class VQVAE(nn.Module):
    def __init__(...):
        self.encoder = Encoder(double_z=False, **ddconfig)
        self.decoder = Decoder(**ddconfig)
        self.quant_conv = torch.nn.Conv2d(self.Cvae, self.Cvae, quant_conv_ks, stride=1, padding=quant_conv_ks//2)
        ...
    def fhat_to_img(self, f_hat: torch.Tensor):
        return self.decoder(self.post_quant_conv(f_hat)).clamp_(-1, 1)

反归一化：.add_(1).mul_(0.5)，将[-1,1]的结果映射到[0,1]的区间

转换回正常色彩空间：在绘图时转换到[0,255]的色彩空间：

chw = chw.permute(1, 2, 0).mul_(255).cpu().numpy()

自此，整个推理过程就结束了。

训练VAR

数据集下载

作者使用ImageNet的2012版本：ImageNet

注意：你需要通过edu相关的邮箱注册并发送请求，才能下载；数据集不能用作商业用途。

文件夹结构如下：

/path/to/imagenet/:
    train/:
        n01440764: 
            many_images.JPEG ...
        n01443537:
            many_images.JPEG ...
    val/:
        n01440764:
            ILSVRC2012_val_00000293.JPEG ...
        n01443537:
            ILSVRC2012_val_00000236.JPEG ...

因为我之前没有用过Imagenet，所以整个我不清楚是否下载正确，我的数据集中val文件夹里全是图片，没有图中的n01440764这样的文件夹，因此我手动新建了若干文件夹，至少是成功运行起来了。

然后将arg_util.py里面的如下位置改成ImageNet文件夹的位置

class Args(Tap):
    data_path: str = '/XXXXXXXXXX/datasets/imagenet'

然后安装官方的指令，即可训练，代码会默认下载vae_ch160v4096z32.pth，是VAE的权重。

# d16, 256x256
torchrun --nproc_per_node=8 --nnodes=... --node_rank=... --master_addr=... --master_port=... train.py \
  --depth=16 --bs=768 --ep=200 --fp16=1 --alng=1e-3 --wpe=0.1
# d20, 256x256
torchrun --nproc_per_node=8 --nnodes=... --node_rank=... --master_addr=... --master_port=... train.py \
  --depth=20 --bs=768 --ep=250 --fp16=1 --alng=1e-3 --wpe=0.1
# d24, 256x256
torchrun --nproc_per_node=8 --nnodes=... --node_rank=... --master_addr=... --master_port=... train.py \
  --depth=24 --bs=768 --ep=350 --tblr=8e-5 --fp16=1 --alng=1e-4 --wpe=0.01
# d30, 256x256
torchrun --nproc_per_node=8 --nnodes=... --node_rank=... --master_addr=... --master_port=... train.py \
  --depth=30 --bs=1024 --ep=350 --tblr=8e-5 --fp16=1 --alng=1e-5 --wpe=0.01 --twde=0.08
# d36-s, 512x512 (-s means saln=1, shared AdaLN)
torchrun --nproc_per_node=8 --nnodes=... --node_rank=... --master_addr=... --master_port=... train.py \
  --depth=36 --saln=1 --pn=512 --bs=768 --ep=350 --tblr=8e-5 --fp16=1 --alng=5e-6 --wpe=0.01 --twde=0.08

注意，官方默认的bs过大，记得调小。

接下来我们以depth=16为例，进行讲解。

main_training.py

这段代码用于执行模型的训练过程。具体功能如下：

初始化参数和环境：
训练循环：
1. 初始化。
2. 遍历每个 epoch，调用 train_one_ep 训练一个 epoch，记录训练统计信息。
3. 更新最佳指标，每 10 个 epoch 或最后一个 epoch 进行验证，并保存模型检查点。
训练结束后：
1. 计算总训练时间，清理资源。
2. 打印最终的训练参数和结果。

def main_training():
    # train
    start_time = time.time()
    best_L_mean, best_L_tail, best_acc_mean, best_acc_tail = 999., 999., -1., -1.
    best_val_loss_mean, best_val_loss_tail, best_val_acc_mean, best_val_acc_tail = 999, 999, -1, -1
    
    L_mean, L_tail = -1, -1
    for ep in range(start_ep, args.ep):
        ...
        
        stats, (sec, remain_time, finish_time) = train_one_ep(      # 训练一个epoch
            ep, ep == start_ep, start_it if ep == start_ep else 0, args, tb_lg, ld_train, iters_train, trainer
        )
        
        ...

        # 在每个训练周期结束时进行验证，并保存模型检查点。
        AR_ep_loss = dict(L_mean=L_mean, L_tail=L_tail, acc_mean=acc_mean, acc_tail=acc_tail)
        is_val_and_also_saving = (ep + 1) % 10 == 0 or (ep + 1) == args.ep
        if is_val_and_also_saving:
            val_loss_mean, val_loss_tail, val_acc_mean, val_acc_tail, tot, cost = trainer.eval_ep(ld_val)
            best_updated = best_val_loss_tail > val_loss_tail
            best_val_loss_mean, best_val_loss_tail = min(best_val_loss_mean, val_loss_mean), min(best_val_loss_tail, val_loss_tail)
            best_val_acc_mean, best_val_acc_tail = max(best_val_acc_mean, val_acc_mean), max(best_val_acc_tail, val_acc_tail)
            AR_ep_loss.update(vL_mean=val_loss_mean, vL_tail=val_loss_tail, vacc_mean=val_acc_mean, vacc_tail=val_acc_tail)
            args.vL_mean, args.vL_tail, args.vacc_mean, args.vacc_tail = val_loss_mean, val_loss_tail, val_acc_mean, val_acc_tail
            print(f' [*] [ep{ep}]  (val {tot})  Lm: {L_mean:.4f}, Lt: {L_tail:.4f}, Acc m&t: {acc_mean:.2f} {acc_tail:.2f},  Val cost: {cost:.2f}s')
            
            if dist.is_local_master():      # 保存检查点
                local_out_ckpt = os.path.join(args.local_out_dir_path, 'ar-ckpt-last.pth')
                local_out_ckpt_best = os.path.join(args.local_out_dir_path, 'ar-ckpt-best.pth')
                print(f'[saving ckpt] ...', end='', flush=True)
                torch.save({
                    'epoch':    ep+1,
                    'iter':     0,
                    'trainer':  trainer.state_dict(),
                    'args':     args.state_dict(),
                }, local_out_ckpt)
                if best_updated:
                    shutil.copy(local_out_ckpt, local_out_ckpt_best)
                print(f'     [saving ckpt](*) finished!  @ {local_out_ckpt}', flush=True, clean=True)
            dist.barrier()

train_one_step()

其中进行训练的是这个：

grad_norm, scale_log2 = trainer.train_step(     # 执行训练
    it=it, g_it=g_it, stepping=stepping, metric_lg=me, tb_lg=tb_lg,
    inp_B3HW=inp, label_B=label, prog_si=prog_si, prog_wp_it=args.pgwp * iters_train,
)

这个代码会进入trainer.py，执行VARTrainer.train_step()

train_step()

forward部分整体代码如下：

# forward
B, V = label_B.shape[0], self.vae_local.vocab_size
self.var.require_backward_grad_sync = stepping

# 处理输入数据
gt_idx_Bl: List[ITen] = self.vae_local.img_to_idxBl(inp_B3HW)       # 将图像转换为输入序列，Encoder+quant_conv 10层，每层尺寸[b,pn^2]
gt_BL = torch.cat(gt_idx_Bl, dim=1)     # 将每一层图像索引拼起来 [b,680]
x_BLCv_wo_first_l: Ten = self.quantize_local.idxBl_to_var_input(gt_idx_Bl)      # [b,679,32] 没了第一层的

# 模型预测
with self.var_opt.amp_ctx:
    self.var_wo_ddp.forward
    logits_BLV = self.var(label_B, x_BLCv_wo_first_l)       # 模型预测，forward [b,680,4096]
    loss = self.train_loss(logits_BLV.view(-1, V), gt_BL.view(-1)).view(B, -1)
    if prog_si >= 0:    # in progressive training  判断是否处于渐进式训练
        bg, ed = self.begin_ends[prog_si]
        assert logits_BLV.shape[1] == gt_BL.shape[1] == ed
        lw = self.loss_weight[:, :ed].clone()
        lw[:, bg:ed] *= min(max(prog_wp, 0), 1)
    else:               # not in progressive training
        lw = self.loss_weight
    loss = loss.mul(lw).sum(dim=-1).mean()  # 使用调整后的权重乘以损失，并计算平均值。

vae_local.img_to_idxBl()

使用encoder和quant_conv（都是卷积）提取特征，然后使用self.quantize.f_to_idxBl_or_fhat转换为码本索引id

class VQVAE(nn.Module):    
    # 将输入图像转换为索引列表。
    def img_to_idxBl(self, inp_img_no_grad: torch.Tensor, v_patch_nums: Optional[Sequence[Union[int, Tuple[int, int]]]] = None) -> List[torch.LongTensor]:    # return List[Bl]
        f = self.quant_conv(self.encoder(inp_img_no_grad))      # [b,3,256,256] -> [b,32,16,16] -> [b,32,16,16]
        return self.quantize.f_to_idxBl_or_fhat(f, to_fhat=False, v_patch_nums=v_patch_nums)    # 特征图转换为索引列表

其中self.quantize.f_to_idxBl_or_fhat的主要功能是将输入特征图 f_BChw 进行多尺度的向量量化，最后返回多层级的量化索引 idx_Bl。其主要步骤如下：

分离输入特征图的梯度，并克隆特征图f_rest，初始化 f_hat 为零张量。
1. f_rest：表示特征图中剩余的信息，初始化是原图，慢慢减去量化过程中提取的特征
2. f_hat：表示重建的特征图信息，初始化为0,慢慢加上量化过程中提取的特征
计算补丁大小: patch_hws=[(1,1),(2,2)......]
多尺度向量量化
1. 对每个补丁大小(ph,pw)，使用下采样插值生成当前尺度的特征向量 z_NC。
2. 计算输入特征和码本权重之间的距离d_no_grad：计算 z_NC 和码本中每个向量的平方和，沿着维度1（特征维度）进行，然后求和
3. d_no_grad.addmm_用于在矩阵乘法的基础上更新一个张量。
  1. 这个操作的目的是在计算每个输入特征向量与码本中每个向量的距离时，考虑它们之间的点积。通过减去两倍的点积，我们可以得到一个距离度量，它结合了特征向量的平方和与点积的信息。这有助于在向量量化过程中找到最接近的码本向量。
  2. $d_{no grad} =\beta \cdot d_{nograd} +\alpha \cdot (z_{NC}\cdot self.embedding.weight.data^T)$ ，alpha 被设置为 -2，beta 被设置为 1，即 $d_{no grad} =d_{nograd} -2\cdot (z_{NC}\cdot self.embedding.weight.data^T)$
4. 沿着维度1（码本维度）找到 d_no_grad 中的最小值的索引，即每个输入特征向量最接近的码本向量。idx_N是码本中的索引，尺寸[b*pn*pn]
5. h_BChw：根据索引 idx_Bhw 从嵌入层（码本）中选取对应的向量，使用双三次插值方法 bicubic 对特征图进行上采样到目标尺寸 (H, W)。
6. self.quant_resi[si/(SN-1)]：根据当前尺度 si 选择一个量化残差处理函数。调整量化特征图 h_BChw，以考虑量化过程中的误差。
7. 将量化特征图 h_BChw 加到重建的特征图 f_hat 上。这是一个原地操作，直接更新 f_hat；从剩余特征图 f_rest 中减去当前量化特征图 h_BChw。这也是一个原地操作，用于更新 f_rest。
返回一个列表 f_hat_or_idx_Bl，包含量化后的量化索引 idx_Bl。

class VectorQuantizer2(nn.Module):
    ...
    # 将输入特征图 f_BChw 转换为量化后的特征图 f_hat 或者索引列表 idx_Bl
    def f_to_idxBl_or_fhat(self, f_BChw: torch.Tensor, to_fhat: bool, v_patch_nums: Optional[Sequence[Union[int, Tuple[int, int]]]] = None) -> List[Union[torch.Tensor, torch.LongTensor]]:  # z_BChw is the feature from inp_img_no_grad
        B, C, H, W = f_BChw.shape
        f_no_grad = f_BChw.detach()     # 将输入特征图分离梯度
        f_rest = f_no_grad.clone()
        f_hat = torch.zeros_like(f_rest)    # 初始化 f_hat 为零张量。
        
        f_hat_or_idx_Bl: List[torch.Tensor] = []
        # 根据 v_patch_nums 计算不同尺度的补丁大小 patch_hws。
        patch_hws = [(pn, pn) if isinstance(pn, int) else (pn[0], pn[1]) for pn in (v_patch_nums or self.v_patch_nums)]    # from small to large
        assert patch_hws[-1][0] == H and patch_hws[-1][1] == W, f'{patch_hws[-1]=} != ({H=}, {W=})'
        
        SN = len(patch_hws)
        for si, (ph, pw) in enumerate(patch_hws): # from small to large
            if 0 <= self.prog_si < si: break    # progressive training: not supported yet, prog_si always -1
            # find the nearest embedding    # 生成当前尺度的特征向量
            z_NC = F.interpolate(f_rest, size=(ph, pw), mode='area').permute(0, 2, 3, 1).reshape(-1, C) if (si != SN-1) else f_rest.permute(0, 2, 3, 1).reshape(-1, C)      # 对特征图 f_rest 进行插值，将其大小调整到 (ph, pw)。
            if self.using_znorm:   # False
                z_NC = F.normalize(z_NC, dim=-1)
                idx_N = torch.argmax(z_NC @ F.normalize(self.embedding.weight.data.T, dim=0), dim=1)
            else:   # 向量量化（Vector Quantization）的过程，其中 z_NC 是输入特征，self.embedding.weight.data 是嵌入层的权重（码本）
                d_no_grad = torch.sum(z_NC.square(), dim=1, keepdim=True) + torch.sum(self.embedding.weight.data.square(), dim=1, keepdim=False)    # [b*pn*pn,4096]计算 z_NC 中每个向量的平方和，沿着维度1（特征维度）进行，并保持维度不变。
                d_no_grad.addmm_(z_NC, self.embedding.weight.data.T, alpha=-2, beta=1)  # (B*h*w, vocab_size)  计算了输入特征和码本权重之间的点积，并将结果加到 d_no_grad 上，用于计算每个特征向量与码本中每个向量的距离。
                idx_N = torch.argmin(d_no_grad, dim=1)  # [b*pn*pn]找到 d_no_grad 中的最小值的索引，即每个输入特征向量最接近的码本向量。
            
            idx_Bhw = idx_N.view(B, ph, pw)     # [b,pn,pn]
            h_BChw = F.interpolate(self.embedding(idx_Bhw).permute(0, 3, 1, 2), size=(H, W), mode='bicubic').contiguous() if (si != SN-1) else self.embedding(idx_Bhw).permute(0, 3, 1, 2).contiguous()
            h_BChw = self.quant_resi[si/(SN-1)](h_BChw)
            f_hat.add_(h_BChw)
            f_rest.sub_(h_BChw)     # 从剩余特征图减去当前向量映射
            f_hat_or_idx_Bl.append(f_hat.clone() if to_fhat else idx_N.reshape(B, ph*pw))
        
        return f_hat_or_idx_Bl

idxBl_to_var_input()

这段代码定义了一个名为 idxBl_to_var_input 的方法，属于 VectorQuantizer2 类。该方法的主要功能是将多尺度的索引列表 gt_ms_idx_Bl 转换为一个张量 f_hat，并生成多个尺度的特征图 next_scales。

具体过程如下：

生成一个全0向量f_hat，其尺寸为[b,32,16,16]
插值特征图：使用双三次插值将每一层特征图插值到目标尺寸 (16,16)，得到h_BChw，尺寸[b,32,16,16]。
将插值后的特征图添加到 f_hat 中。
更新补丁尺寸：更新 pn_next 为下一个尺度的补丁尺寸。
将 f_hat 插值到下一个尺度的尺寸，并将其展平后转置，添加到 next_scales 列表中。next_scales列表中每一个元素尺寸[b,pn*pn,Cvae]=[b,pn*pn,32]，注意：next_scales里不存在pn=1的信息。
返回结果：将 next_scales 列表中的所有张量在指定维度上拼接，返回拼接后的结果。返回结果[b,679,32]，

class VectorQuantizer2(nn.Module):
    def idxBl_to_var_input(self, gt_ms_idx_Bl: List[torch.Tensor]) -> torch.Tensor:
        next_scales = []
        B = gt_ms_idx_Bl[0].shape[0]
        C = self.Cvae
        H = W = self.v_patch_nums[-1]
        SN = len(self.v_patch_nums)
        
        f_hat = gt_ms_idx_Bl[0].new_zeros(B, C, H, W, dtype=torch.float32)      # [b,32,16,16]
        pn_next: int = self.v_patch_nums[0]
        for si in range(SN-1):  # 在多尺度向量量化自编码器中的渐进式训练过程，通过逐尺度地插值和累加特征图，以及处理量化残差，最终构建出完整的重建图像。
            if self.prog_si == 0 or (0 <= self.prog_si-1 < si): break   # progressive training: not supported yet, prog_si always -1
            h_BChw = F.interpolate(self.embedding(gt_ms_idx_Bl[si]).transpose_(1, 2).view(B, C, pn_next, pn_next), size=(H, W), mode='bicubic')     # 使用双三次插值将特征图插值到目标尺寸 (H, W)。
            f_hat.add_(self.quant_resi[si/(SN-1)](h_BChw))      # 将插值后的特征图添加到 f_hat 中。
            pn_next = self.v_patch_nums[si+1]       # 更新 pn_next 为下一个尺度的补丁数量。
            next_scales.append(F.interpolate(f_hat, size=(pn_next, pn_next), mode='area').view(B, C, -1).transpose(1, 2))   # 将 f_hat 插值到下一个尺度的尺寸，并将其展平后转置，添加到 next_scales 列表中。
        return torch.cat(next_scales, dim=1) if len(next_scales) else None    # cat BlCs to BLC, this should be float32

self.var()

使用作者定义的VAR模型进行推理，这里作者使用Teacher Forcing，“teacher forcing input”指的是在训练过程中，模型的输入不仅不是实际的输入数据，而是即“老师”的输出（使VectorQuantizer2得到的的x_BLCv_wo_first_l），在训练过程中，模型被“强迫”去模仿一个“老师”（即真实数据或目标输出）的行为，即使模型的预测可能是错误的。

随机丢弃部分标签:使用 torch.where 随机丢弃部分标签，概率为 self.cond_drop_rate。
1. torch.rand(B, device=label_B.device)：生成一个形状为(B,)的随机数张量，B是批大小，随机数在0到1之间。
2. torch.where：根据条件选择元素，如果随机数小于self.cond_drop_rate（条件dropout率），则使用self.num_classes（通常是一个表示背景或其他类别的固定标签）替换label_B中的相应元素。
生成初始嵌入 sos:使用 self.class_emb 生成初始嵌入 sos，并扩展其维度，尺寸为[b,1,1024]。
根据 self.prog_si 拼接初始嵌入和输入张量:将 sos 和 self.word_embed(x_BLCv_wo_first_l.float()) 拼接在一起，尺寸[b,680,1024]。
添加层级嵌入和位置嵌入:将层级嵌入和位置嵌入添加到 x_BLC 中。
转换张量类型:将 x_BLC、cond_BD_or_gss 和 attn_bias 转换为混合精度类型。
通过多个注意力块前向传播
获取最终的 logits:使用 self.get_logits 获取最终的 logits。
返回 logits:返回最终的 logits。

class VAR(nn.Module):
    def forward(self, label_B: torch.LongTensor, x_BLCv_wo_first_l: torch.Tensor) -> torch.Tensor:  # returns logits_BLV
        """
        :param label_B: label_B
        :param x_BLCv_wo_first_l: teacher forcing input (B, self.L-self.first_l, self.Cvae)
        :return: logits BLV, V is vocab_size
        """
        bg, ed = self.begin_ends[self.prog_si] if self.prog_si >= 0 else (0, self.L)    # 确定输入张量的起始和结束位置。 begin_ends=[(0, 1), (1, 5), (5, 14), (14, 30), (30, 55), (55, 91), (91, 155), (155, 255), (255, 424), (424, 680)]
        B = x_BLCv_wo_first_l.shape[0]
        with torch.cuda.amp.autocast(enabled=False):
            label_B = torch.where(torch.rand(B, device=label_B.device) < self.cond_drop_rate, self.num_classes, label_B)    # 生成一个形状为(B,)的随机数张量，如果随机数小于self.cond_drop_rate（条件dropout率），则使用self.num_classes（1000）替换label_B中的相应元素。
            sos = cond_BD = self.class_emb(label_B)     # embedding [b,1024]
            sos = sos.unsqueeze(1).expand(B, self.first_l, -1) + self.pos_start.expand(B, self.first_l, -1)     # 扩展其维度,加起始位置嵌入
            
            if self.prog_si == 0: x_BLC = sos
            else: x_BLC = torch.cat((sos, self.word_embed(x_BLCv_wo_first_l.float())), dim=1)   # [b,680,1024]将 sos 和 self.word_embed(x_BLCv_wo_first_l.float()) 拼接在一起。
            x_BLC += self.lvl_embed(self.lvl_1L[:, :ed].expand(B, -1)) + self.pos_1LC[:, :ed]   # lvl: BLC;  pos: 1LC  添加层级嵌入和位置嵌入
        
        attn_bias = self.attn_bias_for_masking[:, :, :ed, :ed]      # 计算注意力偏置 attn_bias
        cond_BD_or_gss = self.shared_ada_lin(cond_BD)       # 计算条件嵌入 cond_BD_or_gss。 默认Identity()，即一个不进行任何操作的层。
        
        # hack: get the dtype if mixed precision is used  转换为混合精度类型。
        temp = x_BLC.new_ones(8, 8)
        main_type = torch.matmul(temp, temp).dtype
        
        x_BLC = x_BLC.to(dtype=main_type)
        cond_BD_or_gss = cond_BD_or_gss.to(dtype=main_type)
        attn_bias = attn_bias.to(dtype=main_type)
        
        AdaLNSelfAttn.forward
        for i, b in enumerate(self.blocks):
            x_BLC = b(x=x_BLC, cond_BD=cond_BD_or_gss, attn_bias=attn_bias)
        x_BLC = self.get_logits(x_BLC.float(), cond_BD)     # [b,680,4096]

        return x_BLC    # logits BLV, V is vocab_size

反向传播代码和后面的log部分就不展示了，请感兴趣的读者自行查看，整个train_step的完整代码如下：

    def train_step(
        self, it: int, g_it: int, stepping: bool, metric_lg: MetricLogger, tb_lg: TensorboardLogger,
        inp_B3HW: FTen, label_B: Union[ITen, FTen], prog_si: int, prog_wp_it: float,
    ) -> Tuple[Optional[Union[Ten, float]], Optional[float]]:
        # if progressive training
        self.var_wo_ddp.prog_si = self.vae_local.quantize.prog_si = prog_si
        if self.last_prog_si != prog_si:
            if self.last_prog_si != -1: self.first_prog = False
            self.last_prog_si = prog_si
            self.prog_it = 0
        self.prog_it += 1
        prog_wp = max(min(self.prog_it / prog_wp_it, 1), 0.01)      # 计算当前进度的权重 prog_wp
        if self.first_prog: prog_wp = 1    # no prog warmup at first prog stage, as it's already solved in wp
        if prog_si == len(self.patch_nums) - 1: prog_si = -1    # max prog, as if no prog
        
        # forward
        B, V = label_B.shape[0], self.vae_local.vocab_size
        self.var.require_backward_grad_sync = stepping

        gt_idx_Bl: List[ITen] = self.vae_local.img_to_idxBl(inp_B3HW)       # 将图像转换为输入序列，Encoder+quant_conv 10层，每层尺寸[b,pn^2]
        gt_BL = torch.cat(gt_idx_Bl, dim=1)     # 将每一层图像索引拼起来 [b,680]
        x_BLCv_wo_first_l: Ten = self.quantize_local.idxBl_to_var_input(gt_idx_Bl)      # [b,679,32] 没了第一层的

        with self.var_opt.amp_ctx:
            self.var_wo_ddp.forward
            logits_BLV = self.var(label_B, x_BLCv_wo_first_l)       # 模型预测，forward [b,680,4096]
            loss = self.train_loss(logits_BLV.view(-1, V), gt_BL.view(-1)).view(B, -1)  # [b,680]
            if prog_si >= 0:    # in progressive training  判断是否处于渐进式训练
                bg, ed = self.begin_ends[prog_si]
                assert logits_BLV.shape[1] == gt_BL.shape[1] == ed
                lw = self.loss_weight[:, :ed].clone()
                lw[:, bg:ed] *= min(max(prog_wp, 0), 1)
            else:               # not in progressive training
                lw = self.loss_weight
            loss = loss.mul(lw).sum(dim=-1).mean()  # 使用调整后的权重乘以损失，并计算平均值。
        
        # backward
        grad_norm, scale_log2 = self.var_opt.backward_clip_step(loss=loss, stepping=stepping)
        
        # log
        pred_BL = logits_BLV.data.argmax(dim=-1)        # 预测值计算,取最大值得到预测标签 pred_BL。
        if it == 0 or it in metric_lg.log_iters:
            Lmean = self.val_loss(logits_BLV.data.view(-1, V), gt_BL.view(-1)).item()   # 计算整体的平均损失 Lmean
            acc_mean = (pred_BL == gt_BL).float().mean().item() * 100   # 平均准确率 acc_mean。
            if prog_si >= 0:    # in progressive training  如果 prog_si 大于等于 0，表示正在进行渐进式训练，此时不计算尾部损失和准确率
                Ltail = acc_tail = -1
            else:               # not in progressive training
                Ltail = self.val_loss(logits_BLV.data[:, -self.last_l:].reshape(-1, V), gt_BL[:, -self.last_l:].reshape(-1)).item()
                acc_tail = (pred_BL[:, -self.last_l:] == gt_BL[:, -self.last_l:]).float().mean().item() * 100
            grad_norm = grad_norm.item()
            metric_lg.update(Lm=Lmean, Lt=Ltail, Accm=acc_mean, Acct=acc_tail, tnm=grad_norm)   # 将计算得到的损失和准确率记录到 metric_lg 中。
        
        # log to tensorboard
        if g_it == 0 or (g_it + 1) % 500 == 0:
            prob_per_class_is_chosen = pred_BL.view(-1).bincount(minlength=V).float()   # 计算每个类别的选择概率：通过 bincount 计算每个类别被选择的次数，并进行归一化。
            dist.allreduce(prob_per_class_is_chosen)    # 计算集群使用率
            prob_per_class_is_chosen /= prob_per_class_is_chosen.sum()
            cluster_usage = (prob_per_class_is_chosen > 0.001 / V).float().mean().item() * 100
            if dist.is_master():
                if g_it == 0:       # 记录初始步数的指标：如果当前迭代步数为0，则记录初始步数的集群使用率
                    tb_lg.update(head='AR_iter_loss', z_voc_usage=cluster_usage, step=-10000)
                    tb_lg.update(head='AR_iter_loss', z_voc_usage=cluster_usage, step=-1000)
                kw = dict(z_voc_usage=cluster_usage)
                for si, (bg, ed) in enumerate(self.begin_ends):     # 计算并记录每个分辨率的准确率和交叉熵损失
                    if 0 <= prog_si < si: break
                    pred, tar = logits_BLV.data[:, bg:ed].reshape(-1, V), gt_BL[:, bg:ed].reshape(-1)
                    acc = (pred.argmax(dim=-1) == tar).float().mean().item() * 100
                    ce = self.val_loss(pred, tar).item()
                    kw[f'acc_{self.resos[si]}'] = acc
                    kw[f'L_{self.resos[si]}'] = ce
                tb_lg.update(head='AR_iter_loss', **kw, step=g_it)
                tb_lg.update(head='AR_iter_schedule', prog_a_reso=self.resos[prog_si], prog_si=prog_si, prog_wp=prog_wp, step=g_it)
        
        self.var_wo_ddp.prog_si = self.vae_local.quantize.prog_si = -1
        return grad_norm, scale_log2

训练VAE

代码地址：GitHub - FoundationVision/vaex: 🔥stable, simple, state-of-the-art VQVAE toolkit & cookbook

train_step()

该文件位于vaex-main/trainer.py下单VAETrainer，用于训练VQVAE，训练代码的主体如下：

使用self.vae生成重建的图rec_B3HW，并返回其他损失项 Lq, Le
计算 L1 损失 Lrec，并根据 self.wei_l1 和 self.wei_l2 加权 L1 和 mse损失。
根据条件计算感知损失 Lpip，并组合成总损失 Lnll。
组合所有损失项 Lv。
反向传播和优化

class VAETrainer(object):
    ...
    # @profile(precision=4, stream=open('trainstep.log', 'w+'))
    def train_step(...) -> Tuple[torch.Tensor, Optional[float], Optional[torch.Tensor], Optional[float]]:
        ...

        # [vae loss]
        with maybe_record_function('VAE_rec'):
            with self.vae_opt.amp_ctx:
                self.vae_wo_ddp.forward
                rec_B3HW, Lq, Le, usage = self.vae(inp, ret_usages=loggable)    # 前向传播 VAE，获取重建图像 rec_B3HW 和其他损失项 Lq, Le。
                B = rec_B3HW.shape[0]
                inp_rec_no_grad = torch.cat((inp, rec_B3HW.data), dim=0)
            
            Lrec = F.l1_loss(rec_B3HW, inp)     # 计算 L1 损失 Lrec
            Lrec_for_log = Lrec.data.clone()
            Lrec *= self.wei_l1
            if self.wei_l2 > 0:
                Lrec += F.mse_loss(rec_B3HW, inp).mul_(self.wei_l2)     # 并根据 self.wei_l1 和 self.wei_l2 加权 L1 和 L2 损失。

            
            using_lpips = inp.shape[-2] >= self.lp_reso and self.wei_lpips > 0
            if using_lpips:
                self.lpips_loss.forward
                Lpip = self.lpips_loss(inp, rec_B3HW)       # 根据条件计算感知损失 Lpip
                Lnll = Lrec + self.wei_lpips * Lpip
            else:
                Lpip = torch.tensor(0.)
                Lnll = Lrec
        
        if warmup_disc_schedule > 0:
            with maybe_record_function('VAE_disc'):
                ...
                
                wei_g = warmup_disc_schedule * self.wei_disc
                ...
                
                Lv = Lnll + Lq + self.wei_entropy * Le + wei_g * Lg
        else:
            Lv = Lnll + Lq + self.wei_entropy * Le
            Lg = torch.tensor(0.)
            wei_g = None
        
        with maybe_record_function('VAE_backward'):
            grad_norm_g, scale_log2_g = self.vae_opt.backward_clip_step(stepping=stepping, loss=Lv)

vae

其中vae的代码如下：

class VQVAE(nn.Module):
    def __init__(...):
        self.downsample_ratio = 2 ** (len(ch_mult) - 1)
        
        # 1. build encoder
        self.encoder: CNNEncoder = CNNEncoder(
            ch=ch, ch_mult=ch_mult, num_res_blocks=2, dropout=dropout,
            img_channels=3, output_channels=vocab_width, using_sa=True, using_mid_sa=True,
            grad_ckpt=grad_ckpt,
        )
        # 2. build conv before quant
        self.quant_conv = nn.Conv2d(vocab_width, vocab_width, quant_conv_k, stride=1, padding=quant_conv_k // 2)
        
        # 3. build quant
        self.quantize: VectorQuantizer = VectorQuantizer(vocab_size=vocab_size, vocab_width=vocab_width, vocab_norm=vocab_norm, beta=beta, quant_resi=quant_resi)
        
        # 4. build conv after quant
        self.post_quant_conv = nn.Conv2d(vocab_width, vocab_width, quant_conv_k, stride=1, padding=quant_conv_k // 2)
        
        # 5. build decoder
        self.decoder = CNNDecoder(
            ch=ch, ch_mult=ch_mult, num_res_blocks=3, dropout=dropout,
            input_channels=vocab_width, using_sa=True, using_mid_sa=True,
            grad_ckpt=grad_ckpt,
        )
        self.maybe_record_function = nullcontext
    
    def forward(self, img_B3HW, ret_usages=False):
        f_BChw = self.encoder(img_B3HW).float()     # 通过线性层计算均值，并累加到 diff 中。
        with torch.cuda.amp.autocast(enabled=False):
            VectorQuantizer.forward
            f_BChw, vq_loss, entropy_loss, usages = self.quantize(self.quant_conv(f_BChw), ret_usages=ret_usages)   # 使用 self.quantize 对特征图进行量化。
            f_BChw = self.post_quant_conv(f_BChw)       # 对量化后的特征图进行后处理。
        return self.decoder(f_BChw).float(), vq_loss, entropy_loss, usages      # 使用 self.decoder 对后处理后的特征图进行解码，返回解码后的图像、量化损失、熵损失和使用率。

其中CNNEncoder的架构如下：

class CNNEncoder(nn.Module):
    def __init__(
        self, *, ch=128, ch_mult=(1, 1, 2, 2, 4), num_res_blocks=2, dropout=0.0,
        img_channels=3, output_channels=32, using_sa=True, using_mid_sa=True,
        grad_ckpt=False,
    ):
        super().__init__()
        self.ch = ch
        self.num_resolutions = len(ch_mult)
        self.downsample_ratio = 2 ** (self.num_resolutions - 1)
        self.num_res_blocks = num_res_blocks
        self.grad_ckpt = grad_ckpt
        
        # downsampling
        self.conv_in = torch.nn.Conv2d(img_channels, self.ch, kernel_size=3, stride=1, padding=1)
        
        in_ch_mult = (1,) + tuple(ch_mult)
        self.down = nn.ModuleList()
        for i_level in range(self.num_resolutions):
            block = nn.ModuleList()
            attn = nn.ModuleList()
            block_in = ch * in_ch_mult[i_level]
            block_out = ch * ch_mult[i_level]
            for i_block in range(self.num_res_blocks):
                block.append(BnActConvBnActConv(in_channels=block_in, out_channels=block_out, dropout=dropout))
                block_in = block_out
                if i_level == self.num_resolutions - 1 and using_sa:
                    attn.append(make_attn(block_in, using_sa=True))
            down = nn.Module()
            down.block = block
            down.attn = attn
            if i_level != self.num_resolutions - 1:
                down.downsample = Downsample2x(block_in)
            self.down.append(down)
        
        # middle
        self.mid = nn.Module()
        self.mid.block_1 = BnActConvBnActConv(in_channels=block_in, out_channels=block_in, dropout=dropout)
        self.mid.attn_1 = make_attn(block_in, using_sa=using_mid_sa)
        self.mid.block_2 = BnActConvBnActConv(in_channels=block_in, out_channels=block_in, dropout=dropout)
        
        # end
        self.norm_out = Normalize(block_in)
        self.conv_out = torch.nn.Conv2d(block_in, output_channels, kernel_size=3, stride=1, padding=1)
    
    def forward(self, x):
        h = self.conv_in(x)
        if not self.grad_ckpt or not self.training:
            # downsampling
            for i_level in range(self.num_resolutions):
                for i_block in range(self.num_res_blocks):
                    h = self.down[i_level].block[i_block](h)
                    if len(self.down[i_level].attn) > 0:
                        h = self.down[i_level].attn[i_block](h)
                if i_level != self.num_resolutions - 1:
                    h = self.down[i_level].downsample(h)
            # middle
            h = self.mid.block_2(self.mid.attn_1(self.mid.block_1(h)))
            # end
            h = self.conv_out(F.silu(self.norm_out(h), inplace=True))
        else:
            # downsampling
            for i_level in range(self.num_resolutions):
                for i_block in range(self.num_res_blocks):
                    h = checkpoint(self.down[i_level].block[i_block], h, use_reentrant=False)
                    if len(self.down[i_level].attn) > 0:
                        h = checkpoint(self.down[i_level].attn[i_block], h, use_reentrant=False)
                if i_level != self.num_resolutions - 1:
                    h = checkpoint(self.down[i_level].downsample, h, use_reentrant=False)
            # middle
            h = checkpoint(self.mid.block_1, h, use_reentrant=False)    # PyTorch中的checkpoint函数，这是一种用于减少内存消耗的技术
            h = checkpoint(self.mid.attn_1, h, use_reentrant=False)
            h = checkpoint(self.mid.block_2, h, use_reentrant=False)
            # end
            h = F.silu(self.norm_out(h), inplace=True)
            h = checkpoint(self.conv_out, h, use_reentrant=False)
        
        return h

而BnActConvBnActConv也只是多了归一化和dropout的卷积层

class BnActConvBnActConv(nn.Module):
    def __init__(self, *, in_channels, out_channels=None, dropout): # conv_shortcut=False,  # conv_shortcut: always False in VAE
        super().__init__()
        self.in_channels = in_channels
        out_channels = in_channels if out_channels is None else out_channels
        self.out_channels = out_channels
        
        self.norm1 = Normalize(in_channels)
        self.conv1 = torch.nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=1)
        self.norm2 = Normalize(out_channels)
        self.dropout = torch.nn.Dropout(dropout, inplace=True) if dropout > 1e-6 else nn.Identity()
        self.conv2 = torch.nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1)
        if self.in_channels != self.out_channels:
            self.nin_shortcut = torch.nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=1, padding=0)
        else:
            self.nin_shortcut = nn.Identity()
    
    def forward(self, x):
        h = self.conv1(F.silu(self.norm1(x), inplace=True))
        h = self.conv2(self.dropout(F.silu(self.norm2(h), inplace=True)))
        return self.nin_shortcut(x) + h

其中Downsample2X的代码如下，主要是通过填充实现了2倍的下采样

class Downsample2x(nn.Module):
    def __init__(self, in_channels):
        super().__init__()
        self.conv = torch.nn.Conv2d(in_channels, in_channels, kernel_size=3, stride=2, padding=0)
    
    def forward(self, x):
        return self.conv(F.pad(x, pad=(0, 1, 0, 1), mode='constant', value=0))

对于F.pad(x, pad=(0, 1, 0, 1), mode='constant', value=0)

F.pad是PyTorch中用于对张量进行填充的函数。
pad=(0, 1, 0, 1)：指定了在张量x的四个边界上分别添加的填充大小。具体来说，(0, 1, 0, 1)表示在张量的最后一个维度的开头添加0个单位的填充，在结尾添加1个单位的填充；在倒数第二个维度的开头添加0个单位的填充，在结尾添加1个单位的填充。对于二维卷积，这通常意味着在图像的右边和底边各添加1个像素的填充。
mode='constant'：指定填充模式为常数填充，即用一个固定的值来填充。
value=0：指定填充的值为0。

目的是在这样特定的网络结构，需要实现特征图进行拼接。填充可以确保这些特征图在空间尺寸上是匹配的。

而attn的代码如下，主体内容是通过卷积层获得qkv，然后计算注意力

class AttnBlock(nn.Module):
    def __init__(self, in_channels):
        super().__init__()
        self.C = in_channels
        
        self.norm = Normalize(in_channels)
        self.qkv = torch.nn.Conv2d(in_channels, 3*in_channels, kernel_size=1, stride=1, padding=0)
        self.w_ratio = int(in_channels) ** (-0.5)
        self.proj_out = torch.nn.Conv2d(in_channels, in_channels, kernel_size=1, stride=1, padding=0)
    
    def forward(self, x):
        qkv = self.qkv(self.norm(x))
        B, _, H, W = qkv.shape  # should be B,3C,H,W
        C = self.C
        q, k, v = qkv.reshape(B, 3, C, H, W).unbind(1)
        
        # compute attention
        q = q.view(B, C, H * W).contiguous()
        q = q.permute(0, 2, 1).contiguous()     # B,HW,C
        k = k.view(B, C, H * W).contiguous()    # B,C,HW
        w = torch.bmm(q, k).mul_(self.w_ratio)  # B,HW,HW    w[B,i,j]=sum_c q[B,i,C]k[B,C,j]
        w = F.softmax(w, dim=2)
        
        # attend to values
        v = v.view(B, C, H * W).contiguous()
        w = w.permute(0, 2, 1).contiguous()  # B,HW,HW (first HW of k, second of q)
        h = torch.bmm(v, w)  # B, C,HW (HW of q) h[B,C,j] = sum_i v[B,C,i] w[B,i,j]
        h = h.view(B, C, H, W).contiguous()
        
        return x + self.proj_out(h)

VectorQuantizer

class VectorQuantizer(nn.Module):
    def __init__(
        self, vocab_size: int, vocab_width: int, vocab_norm: bool, beta: float = 0.25, quant_resi=-0.5,
    ):
        ...
        self.embedding = nn.Embedding(self.vocab_size, self.vocab_width)
    ...
    
    def forward(self, f_BChw: torch.Tensor, ret_usages=False) -> Tuple[torch.Tensor, torch.Tensor, torch.Tensor, List[float]]:
        f_BChw = f_BChw.float()
        B, C, h, w = f_BChw.shape
        # find the nearest embedding
        query_NxC = f_BChw.detach().permute(0, 2, 3, 1).reshape(-1, C)  # [b*h*w,c]
        if self.vocab_norm:
            query_NxC = F.normalize(query_NxC, dim=-1)
            idx_N = torch.argmax(query_NxC @ F.normalize(self.embedding.weight.data.T, dim=0), dim=1)   # 计算内积找到最大值索引。
        else:       # 计算欧氏距离并找到最小值索引。
            E_dist = torch.sum(query_NxC.square(), dim=1, keepdim=True) + torch.sum(self.embedding.weight.data.square(), dim=1, keepdim=False)
            E_dist.addmm_(query_NxC, self.embedding.weight.data.T, alpha=-2, beta=1)  # (B*h*w, vocab_size)
            idx_N = torch.argmin(E_dist, dim=1)
        
        prob_per_class_is_chosen = idx_N.bincount(minlength=self.vocab_size).float()    # 根据索引查找对应的嵌入向量，并进行量化残差操作。
        handler = tdist.all_reduce(prob_per_class_is_chosen, async_op=True) if (self.training and dist.initialized()) else None
        
        # look up
        idx_Bhw = idx_N.view(B, h, w)
        fhat_BChw = self.quant_resi(self.embedding(idx_Bhw).permute(0, 3, 1, 2).contiguous())
        
        # calc loss
        vq_loss = F.mse_loss(fhat_BChw.detach(), f_BChw).mul_(self.beta) + F.mse_loss(fhat_BChw, f_BChw.detach())  # 量化损失使用 fhat_BChw.detach()，这意味着在计算梯度时，不会考虑 fhat_BChw 的梯度，而码本损失使用 f_BChw.detach()，这意味着在计算梯度时，不会考虑 f_BChw 的梯度。
        
        # VQVAE: straight through gradient estimation, copy the gradient on fhat_BChw to f_BChw
        fhat_BChw = (fhat_BChw.detach() - f_BChw.detach()).add_(f_BChw)     # 通过这种方式，fhat_BChw 在反向传播时会拥有 f_BChw 的梯度，即使在前向传播中 fhat_BChw 是通过离散的向量量化操作得到的。
        
        # update vocab_usage  更新词汇表的使用率统计信息，记录每次训练的使用情况。
        if handler is not None: handler.wait()
        prob_per_class_is_chosen /= prob_per_class_is_chosen.sum()
        vocab_usage = (prob_per_class_is_chosen > 0.01 / self.vocab_size).float().mean().mul_(100)
        
        if self.vocab_usage_record_times == 0: self.vocab_usage.copy_(prob_per_class_is_chosen)
        elif self.vocab_usage_record_times < 100: self.vocab_usage.mul_(0.9).add_(prob_per_class_is_chosen, alpha=0.1)
        else: self.vocab_usage.mul_(0.99).add_(prob_per_class_is_chosen, alpha=0.01)
        self.vocab_usage_record_times += 1
        
        entropy_loss = 0.0 # todo: not implemented yet
        return fhat_BChw, vq_loss, entropy_loss, (vocab_usage if ret_usages else None)

计算内积找到最大值索引。

idx_N = torch.argmax(query_NxC @ F.normalize(self.embedding.weight.data.T, dim=0), dim=1)   # 计算内积找到最大值索引。

这段代码涉及到在分布式训练环境中计算每个嵌入向量（通常对应于一个类别或词汇表中的一个元素）被选择的概率，并且使用all_reduce操作来同步这些概率。

prob_per_class_is_chosen = idx_N.bincount(minlength=self.vocab_size).float()    # 计算每个嵌入向量被选择的概率。
handler = tdist.all_reduce(prob_per_class_is_chosen, async_op=True) if (self.training and dist.initialized()) else None     # 在多进程训练时，使用 tdist.all_reduce 同步概率。

根据索引查找对应的嵌入向量，并进行量化残差操作。

# look up
idx_Bhw = idx_N.view(B, h, w)
fhat_BChw = self.quant_resi(self.embedding(idx_Bhw).permute(0, 3, 1, 2).contiguous())        # 根据索引查找对应的嵌入向量，并进行量化残差操作。

quant_resi()的代码如下：

残差允许网络学习输入和输出之间的残差（即差异），而不是直接学习输出。而量化残差是在向量量化自编码器（VQ-VAE）中使用的一个概念，它允许模型在量化表示和原始表示之间进行插值，以平衡重建质量和量化误差。

class ResConv(nn.Conv2d):
    def __init__(self, embed_dim, quant_resi):
        ks = 3 if quant_resi < 0 else 1
        super().__init__(in_channels=embed_dim, out_channels=embed_dim, kernel_size=ks, stride=1, padding=ks//2)
        self.resi_ratio = abs(quant_resi)
    
    def forward(self, h_BChw):
        return h_BChw.mul(1-self.resi_ratio) + super().forward(h_BChw).mul_(self.resi_ratio)

量化损失和码本损失

detach()：是一个方法，用于从计算图中分离张量，使其不参与梯度计算。
量化损失和码本损失的计算方式相似，但它们在梯度计算中扮演不同的角色。量化损失使用 fhat_BChw.detach()，这意味着在计算梯度时，不会考虑 fhat_BChw 的梯度，而码本损失使用 f_BChw.detach()，这意味着在计算梯度时，不会考虑 f_BChw 的梯度。
这种设计的目的是为了在训练过程中平衡特征图的重建质量和码本的更新。通过调整 self.beta 的值，可以控制量化损失和码本损失之间的权重，从而影响模型的训练过程和最终的生成质量。

# calc loss
vq_loss = F.mse_loss(fhat_BChw.detach(), f_BChw).mul_(self.beta) + F.mse_loss(fhat_BChw, f_BChw.detach())  # 量化损失使用 fhat_BChw.detach()，这意味着在计算梯度时，不会考虑 fhat_BChw 的梯度，而码本损失使用 f_BChw.detach()，这意味着在计算梯度时，不会考虑 f_BChw 的梯度。

“直通梯度”（Straight-Through Gradient, STG）估计

fhat_BChw.detach()：是重建的特征图，从计算图中分离出来，不追踪梯度。
f_BChw.detach()：是原始的特征图，同样从计算图中分离出来，不追踪梯度。
(fhat_BChw.detach() - f_BChw.detach())：计算重建特征图和原始特征图之间的差异，这两个张量都不参与梯度计算。
.add_(f_BChw)：是一个原地操作，将原始特征图 f_BChw 加到差异上，更新 fhat_BChw 的值。

通过这种方式，fhat_BChw 在反向传播时会拥有 f_BChw 的梯度，即使在前向传播中 fhat_BChw 是通过离散的向量量化操作得到的。这样做的目的是让模型能够学习到如何调整原始特征图 f_BChw，以便在向量量化和重建过程中最小化重建误差。

# VQVAE: straight through gradient estimation, copy the gradient on fhat_BChw to f_BChw
fhat_BChw = (fhat_BChw.detach() - f_BChw.detach()).add_(f_BChw)     # 通过这种方式，fhat_BChw 在反向传播时会拥有 f_BChw 的梯度，即使在前向传播中 fhat_BChw 是通过离散的向量量化操作得到的。

损失函数

重构损失Lrec：通过VQVAE重构的图rec_B3HW和原图比较，计算重构损失

Lrec = F.l1_loss(rec_B3HW, inp)     # 计算 L1 损失 Lrec

mse损失计算的重构损失

if self.wei_l2 > 0:
    Lrec += F.mse_loss(rec_B3HW, inp).mul_(self.wei_l2)     # 并根据 self.wei_l1 和 self.wei_l2 加权 L1 和 L2 损失。

感知损失

self.lpips_loss.forward
Lpip = self.lpips_loss(inp, rec_B3HW)       # 根据条件计算感知损失 Lpip
Lnll = Lrec + self.wei_lpips * Lpip

LPIPS的流程如下

将原始图像和重建图像沿着批次维度拼接，然后标准化
使用预训练好的VGG网络输出5个不同层次的特征图。
遍历VGG网络输出的特征图和对应的线性层
计算原图和重建图的特征之间的平方差，通过1*1的卷积层映射特征差异到损失值，然后计算均值，并累加到 diff 中。

class LPIPS(nn.Module):
    # Learned perceptual metric
    def __init__(self, lpips_path, use_dropout=False):    
        self.net = Vgg16(requires_grad=False)
        self.lins = nn.ModuleList([NetLinLayer(c, use_dropout=use_dropout) for c in [64, 128, 256, 512, 512]])  # 卷积核大小为1的卷积层 c: vgg16 feature dimensions
        
        ...
    
    def forward(self, inp, rec):
        """
        :param inp: image for calculating LPIPS loss, [-1, 1]
        :param rec: image for calculating LPIPS loss, [-1, 1]
        :return: lpips loss (scalar)
        """
        B = inp.shape[0]
        inp_and_recs = torch.cat((inp, rec), dim=0).sub(self.shift).mul_(self.scale_inv)  # 将 inp 和 rec 拼接在一起，并进行去标准化和再标准化处理。first use dataset_mean,std to denormalize to [-1, 1], then use vgg_inp_mean,std to normalize again
        inp_and_recs = self.net(inp_and_recs)   # net:vgg16； len(inp_and_recs) == 5  计算得到5个特征图
        diff = 0.
        for inp_and_rec, lin in zip(inp_and_recs, self.lins):   # 遍历每个特征图和对应的线性层 lin。
            diff += lin.model((normalize_tensor(inp_and_rec[:B]) - normalize_tensor(inp_and_rec[B:])).square_()).mean()     # 计算原图和重建图的特征之间的平方差，通过1*1的卷积层映射特征差异到损失值，然后计算均值，并累加到 diff 中。
        return diff

其中NetLinLayer定义如下：

class NetLinLayer(nn.Module):
    """ A single linear layer which does a 1x1 conv """
    def __init__(self, chn_in, chn_out=1, use_dropout=False):
        super(NetLinLayer, self).__init__()
        layers = [nn.Dropout(), ] if use_dropout else [nn.Identity()]
        layers += [nn.Conv2d(chn_in, chn_out, 1, stride=1, padding=0, bias=False), ]
        self.model = nn.Sequential(*layers)

判别器损失

Lg代表判别器损失，它是生成图像的重建质量的一个指标。在GAN中，这个损失通常用于训练生成器，使其生成的图像能够“欺骗”判别器，即让判别器将生成的图像误判为真实图像。

# 计算生成图像的判别器损失 Lg：  使用数据增强方法 self.daug.aug 对重建图像 rec_B3HW 进行增强，将增强后的图像传递给判别器 self.disc_wo_ddp，并计算其输出的平均值。
self.disc_wo_ddp.forward
Lg = -self.disc_wo_ddp(self.daug.aug(rec_B3HW, fade_blur_schedule), grad_ckpt=False).mean()

disc_wo_ddp代码如下：

这里使用DINO作为判别器。

class DinoDisc(nn.Module):
    def __init__(self, device, dino_ckpt_path, ks, depth=12, key_depths=(2, 5, 8, 11), norm_type='bn', using_spec_norm=True, norm_eps=1e-6):
        ...

        dino_C = self.dino_proxy[0].embed_dim
      
        self.heads = nn.ModuleList([
            nn.Sequential(
                make_block(dino_C, kernel_size=1, norm_type=norm_type, norm_eps=norm_eps, using_spec_norm=using_spec_norm),
                ResidualBlock(make_block(dino_C, kernel_size=ks, norm_type=norm_type, norm_eps=norm_eps, using_spec_norm=using_spec_norm)),
                (SpectralConv1d if using_spec_norm else nn.Conv1d)(dino_C, 1, kernel_size=1, padding=0)
            )
            for _ in range(len(key_depths) + 1) # +1: before all attention blocks
        ])
    
    def forward(self, x_in_pm1, grad_ckpt=False):   # x_in_pm1: image tensor normalized to [-1, 1]
        dino_grad_ckpt = grad_ckpt and x_in_pm1.requires_grad
        FrozenDINOSmallNoDrop.forward
        activations: List[torch.Tensor] = self.dino_proxy[0](x_in_pm1.float(), grad_ckpt=dino_grad_ckpt)    # 用 DINO 模型的前向传播方法，获取激活值列表 activations。
        B = x_in_pm1.shape[0]
        return torch.cat([
            (
                h(act) if not grad_ckpt     # 通过多个头部处理这些激活值
                else torch.utils.checkpoint.checkpoint(h, act, use_reentrant=False)
            ).view(B, -1)
            for h, act in zip(self.heads, activations)      # 遍历激活值和头部
        ], dim=1)  # cat 5 BL => B, 5L

更新判别器

这段代码描述的是一个类似于生成对抗网络（GAN）的训练过程，其中涉及到判别器（discriminator）的损失计算。在GAN中，判别器的目标是区分真实图像和生成的假图像。通过最小化这个损失，判别器可以学习区分真实图像和生成的假图像，而生成器则学习生成越来越逼真的图像。

# [discriminator loss]
if warmup_disc_schedule > 0:
    with maybe_record_function('Disc_forward'):
        for d in self.disc_params: d.requires_grad = True
        with self.disc_opt.amp_ctx:
            self.disc_wo_ddp.forward
            logits = self.disc(self.daug.aug(inp_rec_no_grad, fade_blur_schedule), grad_ckpt=self.disc_grad_ckpt).float()
        
        logits_real, logits_fake = logits[:B], logits[B:]
        acc_real, acc_fake = (logits_real.data > 0).float().mean().mul_(100), (logits_fake.data < 0).float().mean().mul_(100)
        
        Ld = self.d_criterion(logits_real) + self.d_criterion(-logits_fake)
    
    if self.bcr:
        with maybe_record_function('Disc_bCR'):
            with self.disc_opt.amp_ctx:
                self.disc_wo_ddp.forward
                logits2 = self.disc(self.bcr_strong_aug.aug(inp_rec_no_grad, 0.0), grad_ckpt=self.disc_grad_ckpt).float()
            Lbcr = F.mse_loss(logits2, logits).mul_(self.bcr)
            Ld += Lbcr
    else:
        Lbcr = torch.tensor(0.)

5.总结

在这篇博客中，我们深入探讨了Visual AutoRegressive（VAR）模型，这是一种创新的图像生成范式，它通过重新构思自回归学习在图像上的应用，实现了从低分辨率到高分辨率的“next-scale prediction”。

VAR模型不仅在理论上解决了传统自回归模型的局限性，还在实际应用中取得了突破性成果，特别是在ImageNet数据集上，VAR模型在图像质量、推理速度和数据效率等多个维度上超越了现有的扩散模型。此外，VAR模型展现出的零样本泛化能力，使其在图像修复、扩展和编辑等下游任务中表现出色，无需针对特定任务的微调。

VAR模型的提出，不仅推动了自回归模型在计算机视觉领域的发展，也为未来多模态智能的研究提供了新的方向。随着VAR模型的进一步优化和应用，我们有望在图像生成和理解方面实现更多激动人心的突破。
-

如果您对人工智能的最新进展和图像生成技术的革新充满热情，那么这篇关于VAR模型的博客绝对值得您的点赞和关注。如果您对这些内容感兴趣，别忘了收藏这篇文章，以便随时回顾和分享。您的每一次互动都是对我们最大的支持，也是我们继续创作高质量内容的动力。感谢您的参与，让我们一起见证并推动技术的边界！