矩阵快速幂

快速幂基础

点我去看

矩阵基础

矩阵乘法

设A为n行s列，B为s行m列，则结果为C为 :n行m列。n*m
C = A · B；
前提为A的列数与B的行数相同，才可以进行矩阵相乘。
C的第i行第j列的结果为A的第i行与B第j列对应元素之积的和

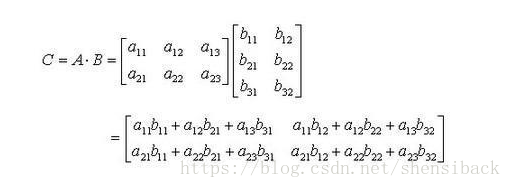
两个数阵的矩阵相乘代码实现：

    //矩阵a*b  a[n][s]*b[s][m] = c[n][m];
void matMulti(int a[][N], int b[][N],  int n) 
{//求a*b，并将相乘结果存入a中
    int temp[N][N];      //先将a与b的乘积存入temp，然后再将其存入a 
    memset(temp, 0, sizeof(temp));
    for(int i = 0;i < n;i++)
    {
        for(int j = 0;j < n;j++)
        for(int k=0;k< n;k++)  
        temp[i][j]+=a[i][k]*b[k][j]; 
    }    //该循环求a*b，并存入了temp 
    for(int i=0;i<n;i++)      //将temp中的值转存入a  
        for(int j=0;j<n;j++)  
            a[i][j]=temp[i][j];     
}

矩阵单位元

矩阵快速幂中，需要与快速幂一样有一个“ans =1”, ，使得ans与任意矩阵相乘的结果都是矩阵本身。即单位矩阵E，特点是除主对角线所有元素为1，其他元素都为0，并且单位矩阵为方阵（即行列相同）例：3*3 与6*6的单位矩阵表示：

$$\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 &1 \end{matrix} \tag{3*3}$$
$$\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{matrix} \tag{6*6}$$
对于任意矩阵 $A_{n*s}$，
我们有 $E_{n*n}*A_{n*s}== A_{n*s}$， $A_{n*s}*E_{s*s} == A_{n*s}$

矩阵相等

矩阵a==b ,当且仅当他们的对应位置的元素完全相同

结合性

A(BC) = (AB)C

矩阵快速幂

求$A^n$:矩阵A为方阵，原理与快速幂相同，如果n的二进制表示最后一位为1，更新ans *= A；然后讲A自乘，n进行以为运算,代码如下：

void matMulti(int a[][s], int b[][m], int n,int m)；//矩阵乘法
void matPow(int a[][N], int n) 
{  //求N*N矩阵a的n次幂  
    int ans[N][N];              //ans用来存放最终结果  
    memset(ans, 0, sizeof(ans));  //将矩阵ans的所有元素置为0  
    for(int i=0; i<n; i++)   ans[i][i] = 1;  //设置单位矩阵  
    while(n)  
    {   if(n&1) matMulti(ans, a, N);   // ans = ans*a；  
        matMulti(a, a, N);            //a = a*a，
        n=n>>1;                  //n = n/2 ;
    }  
    return ;  
}

结构体表示

#include<bits/stdc++.h>
#define ll long long
#define mod 1000000009
using namespace std;
struct Node{
    ll c[2][2];
}ans;
Node mult(Node a,Node b){
    Node c = {0};
    for(int i=0;i<2;i++){
        for(int j=0;j<2;j++){
            for(int k=0;k<2;k++){
                c.c[i][j] += (a.c[i][k] * b.c[k][j]) % mod;
                c.c[i][j] %= mod;
            }
        }
    }
    return c;
}
Node mulPow(ll n){
    Node res = ans;
    if(n<0) return res;
    while(n){
        if(n&1) res = mult(res,ans);
        ans = mult(ans,ans);
        n>>=1;
    }
    return res;
}
void init(){
    ans.c[0][0] = 1;
    ans.c[0][1] = 1;
    ans.c[1][0] = 1;
    ans.c[1][1] = 0;
}
int main(){
    ll n;
    while(cin>>n){
        init();
        Node a = mulPow(n-2);
        cout<<a.c[0][0]*1<<endl;
    }
    return 0;
}

(^o^)/~，理论结束！

【例题】：

求斐波那契数列的第9999999个数，由于这个数值非常大，因此要求计算出其模1000000的值。

#include<bits/stdc++.h> 
using namespace std;
int MOD = 1000000;  
void matMulti(long long a[][2], long long b[][2], int n);
void matPow(long long a[][2], int n) 
{  //求矩阵a的n次幂
    long long ans[2][2];         //ans用来存放最终结果  
    memset(ans, 0, sizeof(ans));  //将矩阵ans的所有元素置为0        
    for(int i=0; i<2; i++)  ans[i][i] = 1;  //设置单位矩阵；  
    while(n)  
    {  
        if(n&1)  matMulti(ans, a, 2);    // ans = ans*a；  
        matMulti(a, a, 2);              //a = a*a
        n = n>>1;                    //n = n/2 
    }
    cout<<ans[1][0]<<endl;  //此处输出ans[1][0]的缘由，见后面**部分
    return ;  
} 

void matMulti(long long a[][2],  long long b[][2],  int n) 
{//求a*b，并将相乘结果存入a中
    long long temp[2][2]; //先将a与b的乘积存入temp，然后再将其存入a 
    memset(temp, 0, sizeof(temp));
    for(int i = 0; i< n; i++)
    {
        for(int j = 0;j < n;j++)
        for(int k=0; k< n; k++)  
        temp[i][j] = (temp[i][j] + a[i][k] * b[k][j]) % MOD; 
    }   //该循环求a*b，并存入了temp 
    for(int i=0; i<n; i++)    //将temp中的值转存入a  
        for(int j=0; j<n; j++)  
        a[i][j] = temp[i][j];   
}
int main()
{
    long long a[2][2] = {1, 1, 1, 0};
    matPow(a, 9999999);
    return 0;
}