【算法分析】分支限界法 一般方法

一、概述

分支限界算法类似于回溯算法。区别是回溯算法进行dfs搜索，而分支限界法进行bfs搜索。

过程：生成当前E节点的全部儿子之后，才从活结点表中选择下一个活结点作为新的E节点。（BFS，可以想想二叉树层序遍历的例子）

活结点：自己已经生成，但是儿子还没开始生成。

E节点：正在扩展的节点。

死节点：儿子节点已经全部生成。

分支限界法的活结点表：FIFO（队列）、LIFO（堆栈）

但是只有这两种活结点表过于死板。比如dfs的下一步就是答案了，但是bfs还要把当前层都扫完才能取下一层找到答案。所以引出了LC检索来优化这个问题。

二、LC-检索（least cost最低成本）

每次把当前节点的子节点放到活结点表中，每次按照成本函数取出成本最小的节点继续拓展。

（具体结合下面的15迷问题来理解LC检索的过程，以及估计函数的定义）

给出一个带有智力的排序函数来决定出当前活结点表中的优先权。（这和棋类游戏中的评估函数很像，对于当前局面给出一个评分）

如果假设我们已经知道答案了，根据答案定义了一个C（x）函数。

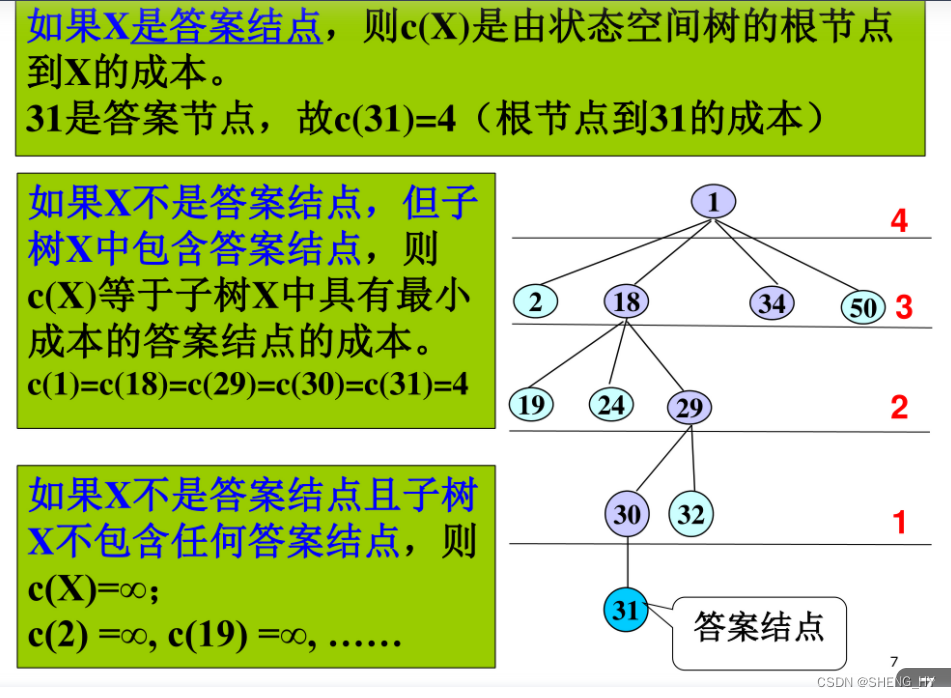
 根据这个成本函数就能较快的找出答案。（直接一部走到结尾还是只在在后一步进行优化？直接走一步，因为其他的节点成本值是∞根本不会选择）

 但实际上如果提前知道了结果是哪个，那也就没必要搜索了，所以给