基于遗传算法的卫星布局优化

原创于 2025-10-17 15:52:10 发布 · 901 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#卫星布局优化 #遗传算法 #Nelder-Mead #PythonOCC

部署运行你感兴趣的模型镜像

2020年国际工业工程与现代技术多会议（FarEastCon）

基于进化优化方法的航天器布局自动化

摘要

提出卫星布局优化设计（SLOD）问题，旨在通过自动化方法生成更优的布局候选方案，供工程师选择。该问题被建模为带有行为约束的三维装箱问题，理论上已被证明属于NP难问题。优化目标包括组件间无干涉、质心偏移最小化以及惯性轴偏差最小化。

为了解决该问题，提出采用带有精化过程的双阶段遗传算法（GA）。在第一阶段，选择组件的承载面和旋转角度；在第二阶段，选择承载面上的位置坐标；在精化过程中，使用Nelder-Mead方法对位置坐标进行修正。

关键词 — 卫星布局优化；遗传算法；内尔德-米德优化；PythonOCC

I. 引言

布局设计是卫星建造的关键步骤之一。自动布局的主要目标是在卫星框架上生成若干组件位置的变体，所有变体均需满足工程要求。卫星布局优化设计（SLOD）问题被定义为带行为约束的三维装箱问题，已被证明是一个NP难问题 [1]。

解决SLOD问题有两种技术类型。一种是将组件转化为数学模型，并应用数值优化方法根据准则（质心位置、主惯性轴对齐、热性能）搜索最优解。这些数学模型在文献中有所描述（滕等，2001b [2]；Sun和Teng 2003[3]；De Sousa和Muraoka2007[4]；Zhang等 2008[5]；Fakoor等 2017[6]；Shafaee等 2017[7]）。已有研究提出了优化方法和算法（Huo等 2007[8]；Zhang等 2008[9]；Wang等 2009[10]；滕等 2010[11]；Xu等 2010[12]；Shi等 2011[13]；Yue等 2011[14]；刘等，2016a [15]；Cui等 2017[16]）。

这些方法适用于可分解为若干二维布局问题的情况。另一类技术是结合计算机辅助设计（CAD）工具与优化算法。该技术已在以下研究中实现（Pühlhofer等 2004[17]；Lau等 2014[18]；Cuco等 2015[19]；Fakoor等 2016[20]；Qin等 2018[21]）。此类技术可保证精度，但需要大量计算能力。

本文其余部分结构如下。在第2节中，描述了SLOD问题，其包含两个目标：最小化质心和惯性轴偏差。接着在第3节中，介绍了布局优化方法。在第4节中，通过案例研究——试验卫星“Orbit craft”验证了所提出方法的可行性。

II. 问题陈述

假设一个卫星模型，其包含可用于部件放置的平面。每个组件的表面均已定义。卫星框架和组件均为具有各自质量参数（质量、质心位置和惯性轴）的实体模型。同时假设卫星框架按照基本技术坐标系(BTCS)定向。卫星模型可具有承重面，其位置不排除位于其上的组件之间发生干涉的可能性。每个承重面由形心、法线、自身的X轴方向以及尺寸定义：

$$
M_w = [O_w, \bar{N}_w, \bar{X}_w, L, H]
$$

组件具有自身的坐标系，其原点位于表面形心的底部，Z轴沿该表面法线方向指向组件内部。质心不一定与Z轴重合。

A. 设计变量

为每个组件定义的设计变量如下：允许的承重面索引、组件绕Z轴的旋转角、组件基准点在表面上的x和y位置坐标。x和y的范围为[-1；1]，当x和y等于0时，组件基准点位于表面形心；当x和y等于1或-1时，组件位于边缘。

$$
X = {X_1, X_2, …, X_n} = {X_i = (m_i, \alpha_i, x_i, y_i) | i = 1,2,…,N}
$$

其中：
- $ m_i $ 是第i个组件的面索引；
- $ a_i = 0 $ 或 1;
- $ x = [-1, 1] $;
- $ y = [-1, 1] $.

B. 布局约束

基本布局约束是组件形状不应相交，且不应与卫星框架相交。

静态稳定性约束意味着航天器质心应位于允许范围内。基于此，该约束表示实际质心与预期质心之间的距离应小于最大允许偏移。静态稳定性约束可表示为：

$$
\sqrt{|x_r - x_p|^2 + |y_r - y_p|^2 + |z_r - z_p|^2} - \delta c \leq 0
$$

动态平衡约束意味着整个航天器的惯性轴(X, Y, Z)应与基本技术坐标系的轴(Xp, Yp, Zp)平行，偏转角不应超过 $\delta \theta$。动态平衡约束可以表示为：

$$
\max\left((\hat{X}, X_p), (\hat{Y}, Y_p), (\hat{Z}, Z_p)\right) - \delta \theta \leq 0
$$

描述单个组件位置的约束，这些约束与单个组件的要求相关。其中一些组件允许位于框架内部，另一些必须从外部可接触，还有一些组件（如偏航速率传感器）允许位于法线与基本轴之一平行的表面上。

$$
\bar{X} = {X_i = (m_i, \alpha_i, x_i, y_i) | i = 1,2,…,N}
$$

$$
m_i \in [p_0, p_1, …, p_t]_i (\forall p_t \in [1,2,…,M])
$$

其中M为允许布置的面的数量。

C. 优化目标

对于每个卫星版本，都会计算参数向量：

$$
\bar{U}(X) = [U_1(X), U_2(X), U_3(X), U_4(X)]
$$

其中：
- $ U_1(X) $ 是预期质心之间的距离计算得出；
- $ U_2(X) $ 是惯性轴与BTCS轴之间偏差的最大值；
- $ U_3(X) $ 是组件间的交集体积；
- $ U_4(X) $ 是组件与卫星框架的交集体积。

目标函数通过参数向量和权重向量A的标量积计算得出：

$$
f(X) = \bar{U}(X) \cdot \bar{A} = A_1U_1(X) + A_2U_2(X) + A_3U_3(X) + A_4U_4(X)
$$

权重系数定义如下：

$$
\bar{A} = [A_1, A_2, A_3, A_4]
$$

$$
A_1 = \frac{a}{\delta c_1}
$$

$$
A_3 = a_3
$$

$$
A_4 = a_4
$$

根据任务的具体情况选择a1, a2, a3, a4的值。

因此，该优化问题归结为求函数 $ f(X) $ 的最小值：

$$
Min(\bar{U}(X) \cdot \bar{A})
$$

D. 设计变量计算

计算由PythonOCC执行。PythonOCC是面向Python编程语言的三维 CAD/CAE/PLM开发框架。它提供了高级拓扑与几何操作、数据交换（STEP、IGES、STL导入/导出）、基于GUI的可视化（wx、Qt）以及jupyter notebook渲染等功能。PythonOCC基于开源三维CAD内核OCE项目构建。

形状的平移与旋转通过gp_Trsf类的方法实现。Perfom函数用于将组件和框架组合成一个整体对象。惯性张量Mat通过Group_Grops类中的MatrixOfInertia()函数计算，该函数通过Value(i, j)返回值，其中i, j = 1, 2, 3：

$$
M_{ij} = mat.value(i,j)
$$

基于此计算惯性轴偏差：

$$
\hat{X}, X_p = \arccos\left( \frac{X_1M_{11} + X_2M_{12} + X_3M_{13}}{\sqrt{X_1^2 + X_2^2 + X_3^2} \sqrt{M_{11}^2 + M_{12}^2 + M_{13}^2}} \right)
$$

$$
\hat{Y}, Y_p = \arccos\left( \frac{Y_1M_{21} + Y_2M_{22} + Y_3M_{23}}{\sqrt{Y_1^2 + Y_2^2 + Y_3^2} \sqrt{M_{21}^2 + M_{22}^2 + M_{23}^2}} \right)
$$

$$
\hat{Z}, Z_p = \arccos\left( \frac{Z_1M_{31} + Z_2M_{32} + Z_3M_{33}}{\sqrt{Z_1^2 + Z_2^2 + Z_3^2} \sqrt{M_{31}^2 + M_{32}^2 + M_{33}^2}} \right)
$$

然后 $ U_1 $ 被定义为最大散度：

$$
U_1 = \max\left((\hat{X}, X_p), (\hat{Y}, Y_p), (\hat{Z}, Z_p)\right)
$$

质心“cog”由同一类中的bnCentreOfMass()函数计算得出：

$$
x_p, y_p, z_p = cog.Coord()
$$

$ U_2 $ 按如下方式计算：

$$
U_2 = \sqrt{|x_r - x_p|^2 + |y_r - y_p|^2 + |z_r - z_p|^2}
$$

在循环步骤中计算组件的相交部分，其中通过 BRepAlgoAPI_Section() 类中的 brepgprop_LinearProperties 函数确定另外两个组件的公共体积，该体积在循环步骤中累加，然后返回其一半值。

与框架的相交通过相同的方法计算，不同之处在于与框架的相交是在循环步骤中计算的。

III. 布局约束计算方法

本节提出了结合Nelder-Mead方法精化的两步遗传算法，用于处理不重叠约束、静态稳定性约束和动态平衡约束。

A. 面上组件布局的递归算法

在航天器框架上的布局过程中，每个面的组件集合被形成。存在一些简化：组件被转换为矩形，其尺寸ai, bi等于组件的尺寸；面被简化为具有正交边和面积Swall的多边形。

首先，通过区域比较来检查位置的可能性：

$$
S_{wall} \geq \sum_{i=1}^{N} a_{i,wall} b_{i,wall}
$$

其中N 是属于“壁面”的组件数量。

如果检查未成功，则会生成一个新的变体。

然后使用递归算法：
1) 寻找可用于放置的多边形；
2) 多边形通过若干变体被划分为最大面积的矩形；
3) 从最小面积矩形开始，依次遍历矩形，进一步遍历分割变体和组件（从底面最大面积的组件开始），直到组件无法放入矩形中为止。同时也会检查组件旋转90度的变体；
4) 当所有组件都位于面多边形上时，递归停止。

算法的框图如图1所示。

示意图0

示意图1

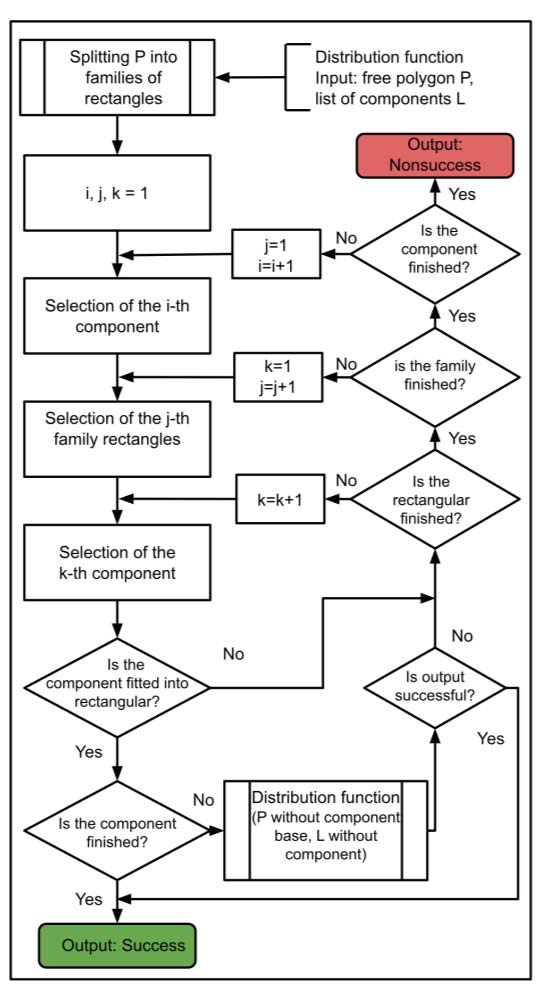
B. 进化算法

遗传算法（GA）与优化算法结合使用，其中GA找到粗略结果，优化算法对其进行细化。基本结构包括两个GA阶段，第一阶段为每个组件选择面索引和旋转，第二阶段选择位置坐标。Nelder-Mead算法用作优化算法，以精化位置坐标。

在每个模块中，参数向量U与阈值进行比较。如果满足以下条件，则算法停止：

$$
U_1 \leq a_1 \
U_2 \leq a_2 \
U_3 = U_4 = 0
$$

第一代种群通过随机方法生成：组件的索引从允许的索引范围内选取，旋转从0或1中选取（1对应90度旋转角），位置坐标值介于-1和1之间。

这样会生成多个向量。向量的总数为种群大小 - Pop_Size。

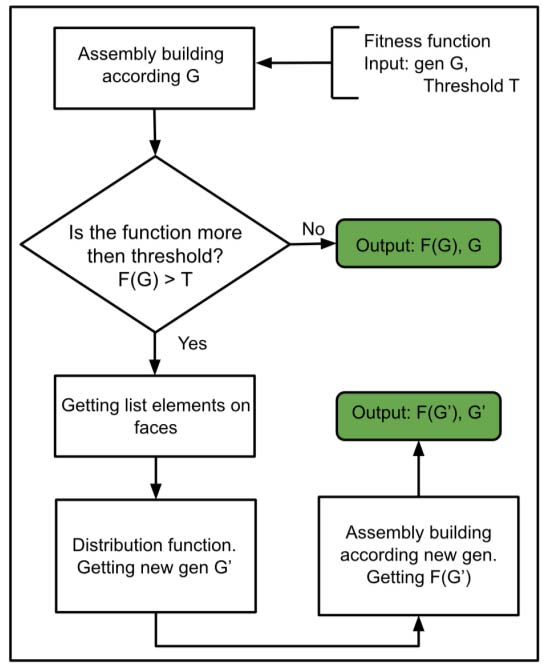
在基因处理开始时，根据变量向量构建装配。如果目标函数的值大于阈值T，则在保存面索引的同时使用分配算法。如果分配算法显示使用这些面索引无法实现装配，则在本地生成新基因。新基因由分配算法进行检查和编辑。

在这两种情况下，处理函数返回编辑后的基因，然后替换种群中的基因。分配完成后，重新构建装配，并重新计算目标函数的值并予以保留。选择适应度函数最小的基因，其数量由精英比例参数定义。

$$
N_{parents} = ElitistFraction \cdot PopSize
$$

最佳基因被复制到新种群中，其他基因则作为第一代基因生成。

在第二阶段，基因通过复制上一代的最佳基因并对其位置坐标变量进行变异而生成。其中，未发生变化的副本（父代）将在新一代中被保留。

适应度函数的计算方式与第一阶段相同。因此，如果目标函数超过阈值，则使用重新分配，并将编辑后的基因返回到种群中。

Nelder-Mead方法用于精化。该方法（约翰·尼德爾和羅傑·米德，1965年）是一种常用的数值方法，用于在多维空间[25]中寻找目标函数的最小值或最大值。它是一种直接搜索法（基于函数比较），通常应用于导数可能未知的非线性优化问题。

此阶段仅编辑位置坐标。

示意图2

示意图3

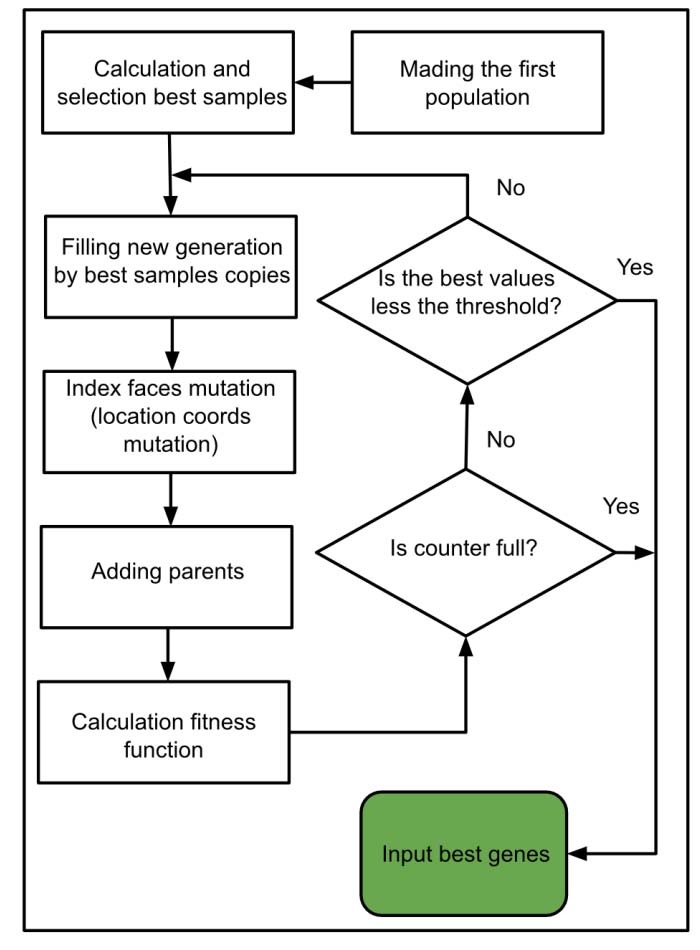
IV. 案例研究 “ORBITCRAFT”

A. 测试问题描述

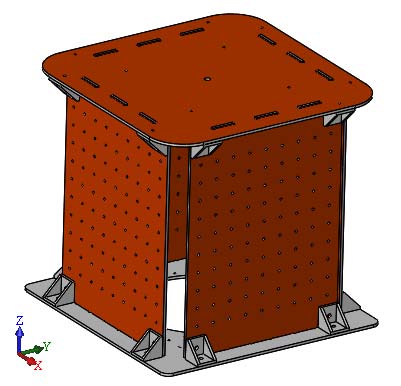
航天器由套件框架（6个壁，如图9所示）和16个组件（表1）组成。组件可以放置在外部面上，但飞轮只能放置在顶面上。可用表面如图4 (a, b)所示。

框架尺寸为266毫米、266毫米、254毫米，质量为1.01千克。基本技术坐标轴的方向如图4所示，基准点位于框架的形心处。质心起始位置为(0; 0; 6.3)。惯性张量见表2。期望质心：(0; 0; 0)。质心最大允许偏差为0.5毫米。惯性轴最大允许偏差为30角分。

表II. 航天器框架的惯性张量

Lxx = 0.16（千克/米²）	Lxy = 0.0（kg/m²）	Lxz = 0.0（千克/米²）
Lyx = 0.0（千克/米²）	Lyy = 0.16 (kg/m²)	Lyz = 0.0 （千克/米²）
Lzx = 0.0（千克/米²）	Lzy = 0.0 (kg/m²)	Lzz = 0.16（千克/米²）

表III. 组件的特性 TS

设备	质量，克	а，毫米	b，毫米	h，毫米
所有 Sep WS16 _ _	228.84	150	90	94.3
Base_sape	235.18	150	90	60.5
Batterry_WS16	213.92	160	116	61.4
Camera_WS16	65.4	94	58	43.8
Camera2_WS16	65.4	94	58	43.8
DAV_WS16	64.47	94	58	39
DAV2 WS16_	73.41	94	58	39
DAV3 WS16_	74.57	94	58	39
磁力计	64.47	94	58	39
飞轮	283.37	155	155	84
无线电 WS16_	64.8	94	58	39
Sep	40.41	88	44	35.3
太阳能_电池_WS16	64.7	94	58	39
太阳辐射计_	64.53	94	58	39
UKV	64.47	94	58	39
Vch 转换器 WS16 _ _	64.49	94	58	39

表IV. 研究的常量值

参数	值	定义
种群大小	8	种群大小
$ Elitist Fraction $	0.1	确定数量的参数种群中幸存者的数量
$ \delta c $	0.5	质心最大允许偏差 , mm
$ \delta \theta $	0.5	惯性轴最大允许偏差，度
n ‐ 的多重性结合	2	将自由多边形分割为矩形族
$ a_1 $	0.001	权重因子
$ a_2 $	0.001	权重因子
$ a_3 $	0.001	权重因子
$ a_4 $	0.001	权重因子
step	0.01	邻域搜索半径初始步长
阿尔法	1	算法参数
伽马	2	算法参数
rho	-0.5	算法参数
西格玛	0.05	算法参数

B. 结果与讨论

在表3中对常数进行了一些实验，其中前两个遗传算法步骤的代数发生了变化。研究目的是验证该方法在解决SLOD问题上的适用性。

研究成果通过所有计算装配体的数量进行评估，这可以显示实验所消耗的计算资源。然而，部分样本是并行计算的，因此应通过最后一代的索引来评估所花费的时间。

如表4‐5所示，在遗传算法步骤中代数最少的实验中获得了最经济且最快的结果。然而，由于GA和Nelder-Mead算法是启发式的，因此无法保证获得同样快速的结果。

然而，实验结果表明，“Orbitcraft” SLOD问题可以通过所提出的方法解决。

表V. 研究结果

№	Ⅰ	ⅠⅠ	ⅠⅠⅠ	U1，毫米	U2，度	最后一代的适应度函数	Index结果	所有计算装配体的数量
1	20	50	900	-0,43	0,498	0,001935	198	773
2	50	50	900	0,04	0,498	0,00108	492	1307
3	100	50	900	0,13	0,489	0,001279	613	1828
4	150	50	900	-0,04	0,498	0,001079	476	2091
5	200	50	900	0,36	0,239	0,001135	561	2576
6	20	100	1000	0,33	0,498	0,001741	225	1200
7	20	150	1000	0,14	0,461	0,001212	453	1828
8	20	200	1000	0,04	0,453	0,001002	379	2154
9	20	250	1000	0,42	0,175	0,001223	336	2511

表六。绘图研究结果

测试编号1 (20_50_900) 世代遗传算法	测试编号1 (20_50_900) 内尔德_mead
测试编号5 (200_50_900) 世代遗传算法	测试编号5 (200_50_900) 内尔德_mead
测试编号6 ( 20_100_1000 ) 世代遗传算法	测试编号6 ( 20_100_1000 ) 内尔德_mead
测试编号9 (20_250_1000) 世代遗传算法	测试编号9 (20_250_1000) 内尔德_mead