C++篇（20）并查集

1、并查集的原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按照一定的规律将同一组元素的集合合并，在此过程中要反复用到查询某一个元素归属于哪个集合的运算。适用于描述这类问题的抽象数据类型称为并查集。

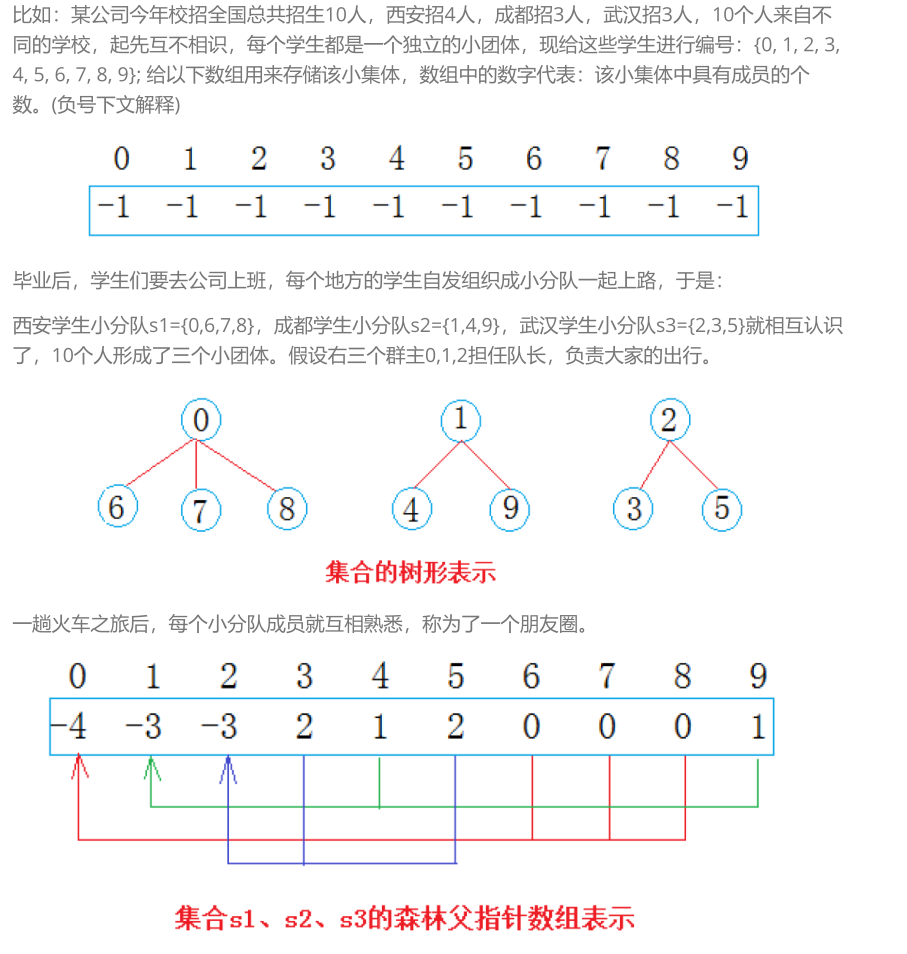
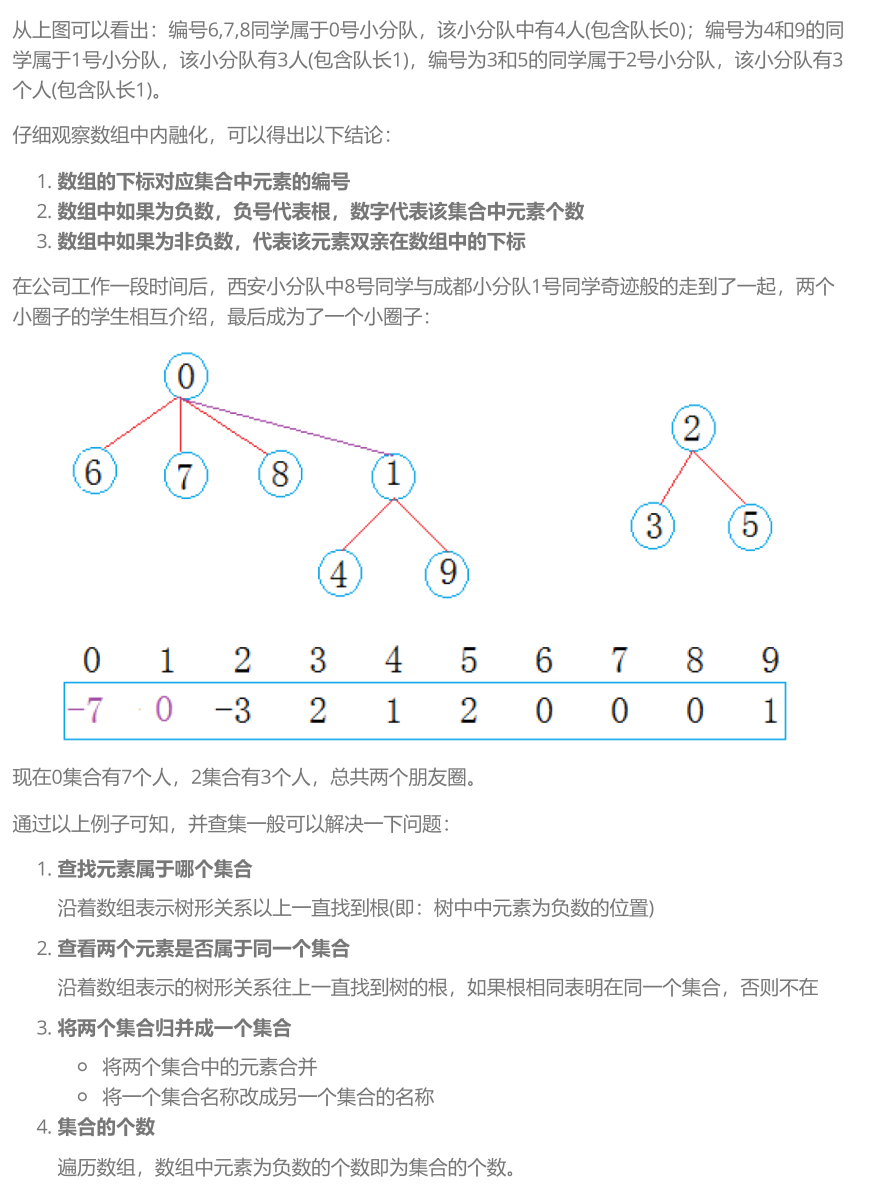
2、并查集的实现

#pragma once
#include <vector>
#include <map>

class UnionFindSet
{
public:
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{ }

	void Union(int x1, int x2)
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		// 如果本身在一个集合就没必要合并了
		if (root1 == root2)
			return;

		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
	}

	int FindRoot(int x)
	{
		int parent = x;
		while (_ufs[parent] >= 0)
		{
			parent = _ufs[parent];
		}

		return parent;
	}

	bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);
	}

	size_t SetSize()
	{
		size_t size = 0;
		for (size_t i = 0;i < _ufs.size();++i)
		{
			if (_ufs[i] < 0)
			{
				++size;
			}
		}

		return size;
	}

private:
	vector<int> _ufs;
};

如果题目中并没有用编号来表示数据，那么在实现并查集时可以用map建立映射关系。

template<class T>
class UnionFindSet
{
public:
	UnionFindSet(const T* a, size_t n)
	{
		for (size_t i = 0;i < n;i++)
		{
			_a.push_back(a[i]);
			_indexMap[a[i]] = i;
		}
	}
private:
	vector<T> _a;  // 编号找人
	map<T, int> _indexMap;  // 人找编号
};

3、并查集的应用

class Solution {
public:
    bool equationsPossible(vector<string>& equations) 
    {
        vector<int> ufs(26, -1);
        auto findRoot = [&ufs](int x)
        {
            while(ufs[x] >= 0)
            {
                x = ufs[x];
            }
            return x;
        };

        // 第一遍，先把相等的值加到一个集合中
        for(auto& str : equations)
        {
            if(str[1] == '=')
            {
                int root1 = findRoot(str[0] - 'a');
                int root2 = findRoot(str[3] - 'a');
                if(root1 != root2)
                {
                    ufs[root1] += ufs[root2];
                    ufs[root2] = root1;
                }
            }
        }

        // 第二遍，判断不相等的在不在同一个集合，在就相悖了
        for(auto& str : equations)
        {
            if(str[1] == '!')
            {
                int root1 = findRoot(str[0] - 'a');
                int root2 = findRoot(str[3] - 'a');
                if(root1 == root2)
                {
                    return false;
                }
            }
        }

        return true;
    }
};