hihoCoder1324

最新推荐文章于 2018-08-01 16:01:27 发布

sdnuzsj

最新推荐文章于 2018-08-01 16:01:27 发布

阅读量218

点赞数

CC 4.0 BY-SA版权

分类专栏： ------------数学------------

本文链接：https://blog.youkuaiyun.com/sdnuzsj/article/details/78064124

------------数学------------ 专栏收录该内容

11 篇文章

订阅专栏

本文介绍了一种通过递归算法实现的希尔伯特曲线坐标到顶点序号转换的方法。针对给定的分形曲线阶数及坐标，文章详细解释了如何计算出该坐标对应顶点在曲线上的位置序号。

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

希尔伯特曲线是以下一系列分形曲线 H_n 的极限。我们可以把 H_n 看作一条覆盖 2ⁿ × 2ⁿ 方格矩阵的曲线，曲线上一共有 2ⁿ × 2ⁿ 个顶点(包括左下角起点和右下角终点)，恰好覆盖每个方格一次。

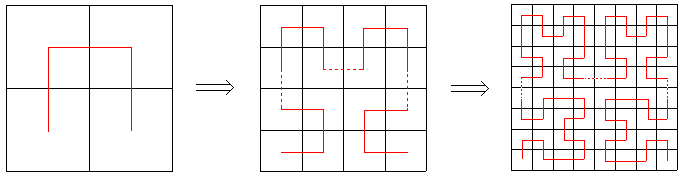
H_n(n > 1)可以通过如下方法构造：

1. 将 H_n-1 顺时针旋转90度放在左下角

2. 将 H_n-1 逆时针旋转90度放在右下角

3. 将2个 H_n-1 分别放在左上角和右上角

4. 用3条单位线段把4部分连接起来

对于 H_n 上每一个顶点 p ，我们定义 p 的坐标是它覆盖的小方格在矩阵中的坐标，定义p 的序号是它在曲线上从起点开始数第几个顶点。给定 p 的坐标，你能算出 p 的序号吗？

输入

输入包含3个整数 n , x , y 。 n 是分形曲线的阶数，(x,y)是 p 的坐标。

1 ≤ n ≤ 30

1 ≤ x, y ≤ 2ⁿ

输出

p 的序号。

样例输入

3 6 1

样例输出

分治或说成递归，把大问题分解为一个个的小问题。此题找到坐标转移方程就可轻松求解。

具体看代码。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long LL;


LL fun(LL n,LL x,LL y)
{
    if(n==1)
    {
        if(x==1&&y==1) return 1;
        if(x==1&&y==2) return 2;
        if(x==2&&y==2) return 3;
        if(x==2&&y==1) return 4;
    }
    else
    {
        if(x<=(LL)pow(2,n-1)&&y<=(LL)pow(2,n-1))
        {
            LL t;
            t=x;
            x=y;
            y=t;
            return fun(n-1,x,y);
        }
        if(x<=(LL)pow(2,n-1)&&y>(LL)pow(2,n-1))
        {
            y-=(LL)pow(2,n-1);
            return fun(n-1,x,y)+(LL)pow(2,n-1)*(LL)pow(2,n-1);
        }
        if(x>(LL)pow(2,n-1)&&y>(LL)pow(2,n-1))
        {
            x-=(LL)pow(2,n-1);
            y-=(LL)pow(2,n-1);
            return fun(n-1,x,y)+(LL)pow(2,n-1)*(LL)pow(2,n-1)*2;
        }
        if(x>(LL)pow(2,n-1)&&y<=(LL)pow(2,n-1))
        {
            x-=(LL)pow(2,n-1);
            LL t1=x;
            LL t2=y;
            x=-t2+(LL)pow(2,n-1)+1;
            y=-t1+(LL)pow(2,n-1)+1;
            return fun(n-1,x,y)+(LL)pow(2,n-1)*(LL)pow(2,n-1)*3;
        }
    }
}

int main()
{
    LL n,x,y;
    while(~scanf("%lld%lld%lld",&n,&x,&y))
    {
        printf("%lld\n",fun(n,x,y));
    }
    return 0;
}