


例1-1 图一
自感: 电流和电压同相,则
电流和电压同相,则  为正,不带负号;
为正,不带负号;
互感:标有*的为互感电压的正极, 的互感电压与
的互感电压与 同相;则
同相;则 也为正;
也为正;
得
自感: 电流和电压同相,则
电流和电压同相,则  为正,不带负号;
为正,不带负号;
互感:标有*为互感电压的正极, 的互感电压与
的互感电压与 同相;则
同相;则 也
也
为正;
得:
图二:
自感: 电流和电压同相,则
电流和电压同相,则  为正,不带负号;
为正,不带负号;
互感:标有*为互感电压的正极, 的互感电压与
的互感电压与 反相;则
反相;则 为负;
为负;
自感: 电流和电压同相,则
电流和电压同相,则  为正,不带负号;
为正,不带负号;
互感:标有*为互感电压的负极, 的互感电压与
的互感电压与 反相;则
反相;则 为负;
为负;
图三:
自感: 电流和电压同相,则
电流和电压同相,则  为正,不带负号;
为正,不带负号;
互感:标有*为互感电压的正极, 的互感电压与
的互感电压与 正相;则
正相;则 为正;
为正;
自感: 电流和电压反相,则
电流和电压反相,则  为负,带负号;
为负,带负号;
互感:标有*的为互感电压的正极, 的互感电压与
的互感电压与 反相;则
反相;则 为负;
为负;
图四
自感: 电流和电压反相,则
电流和电压反相,则  为负,带负号;
为负,带负号;
互感:标有*为互感电压的负极, 的互感电压与
的互感电压与 反相;则
反相;则 为负;
为负;
自感: 电流和电压反相,则
电流和电压反相,则  为负,带负号;
为负,带负号;
互感:标有*的为互感电压的负极, 的互感电压与
的互感电压与 反相;则
反相;则 为负;
为负;
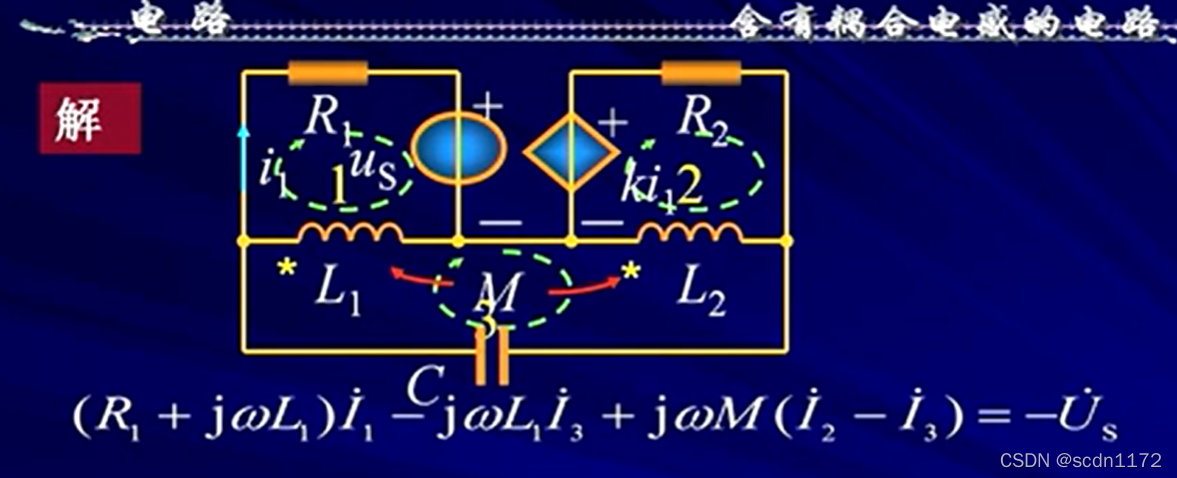
列写回路方程:
回路1:
 :电阻电压
:电阻电压
 :
: 的自感电压
的自感电压
回路3的L1自感电压:
回路3中的 对
对 产生的互感:
产生的互感:
回路2中的 对
对 产生的互感:
产生的互感:
回路2,3不再多缀述:

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








