[matlab实践应用]matlab实现读取xls表格并三次样条插值拟合压杆稳定实验数据

最新推荐文章于 2023-05-14 15:06:35 发布

程序菜鸟一只

最新推荐文章于 2023-05-14 15:06:35 发布

阅读量2.3k

点赞数 2

文章标签： matlab 力学

本文链接：https://blog.youkuaiyun.com/sbsbsb666666/article/details/121664675

版权

上一期给大家发布了“MATLAB三次样条插值拟合实验数据”，这一次我们就来看一下三次样条在实验中的工程应用：

在本文中，我会直接使用Spline_3来进行三次样条插值拟合：Spline_3是我上一篇文章里三次样条拟合数据很方便的一个函数

三次样条插值的详细讲解和Spline_3函数（包括len）来源请参见我的上一篇文章：[数值分析拟合]Matlab三次样条插值拟合数据

一、实验内容：压杆稳定实验

材料力学中，对于部件的强度校核问题，需要综合考虑强度，刚度和稳定性问题，其中稳定性是一个很重要的课题，对于材料力学在压杆稳定方面的分析，可使用欧拉公式来解决

欧拉公式简介:对于大柔度杆（ $\lambda<\lambda_p$ ,其中 $\lambda=\mu\frac{l}{i},i=\surd(I/A), I=\frac{bh^3}{12}$ ）其中I为绕z轴的惯性矩（以宽的那一边为b，更容易失稳）,试样（长方形截面）宽b，高h，i为惯性半径， $\mu$ 为等效长度系数，对于两端铰支的杆，等效长度系数为1，两端固定的杆，长度系数为0.5，一段铰支一段固定的杆长度系数为0.7（较精确值约0.707），而 $\lambda_p$ 由材料性质等决定，可以查表获得

（1）杆的理论最大应力的计算：

本实验中，均认为实验中的杆件为大柔度杆

满足欧拉公式： $F_{cr}=\frac{\pi^2EI}{(\mu l)^2}$ ，E为材料的弹性模量。

其中，Fcr是临界压力，压力超过临界压力后，杆件即会发生不可恢复的塑性变形

（2）杆实际应力的测量：

对于压弯状态的杆，在逐步施加压力时，做出杆的反力和两端的位移量图，在临界压力处，杆件的反力会趋向于一个极值，做出反力的渐近线，即得到实验确定的极限应力值。

二、实验数据

1）补充数据

试样（条状）宽b=19.6mm,高h=2mm

弹性模量E=210Gpa

对于两端固定的杆， $\mu=0.5,l_1=366mm$

上端固定，下端铰支的杆 $\mu=0.7,l=378mm$

下端固定，上端铰支的杆 $\mu=0.7,l=382mm$

两端铰支的杆： $\mu=$ 1,l=395mm

2）原始压力数据实验表格：百度网盘

提取压杆稳定实验数据

提取码：c3xy

其中以端点位移量（也就是上端点的下降量）为x坐标，以压力为纵坐标（由压力传感器测得），绘制出杆的受压情况

将表格作为data.xls保存在该程序的文件夹下

三、代码

clf
data=xlsread('data.xls');
%-----读取数据-----------
t1=data(:,1);
F1=data(:,2);
t2=data(:,1);t2=t2(1:21,:);
F2=data(:,3);F2=F2(1:21,:);
t3=data(:,1);t3=t3(1:30,:);t4=t3;
F3=data(:,4);F3=F3(1:30,:);
F4=data(:,5);F4=F4(1:30,:);
%----------------------------------------
figure(1)
subplot(1,2,1)
hold on 
plot(t1,F1,'-b','Linewidth',0.2);
plot(t2,F2,'-r')
plot(t3,F3,'-k')
plot(t4,F4,'-c')
axis([0,0.9,0,800])
xlabel('端点的位移量')
ylabel('压力（N）')
legend('两端固定','上固下铰','上铰下固','两端铰支','location','northwest')

subplot(1,2,2)
hold on
[t_1,F_1]=Spline_3(t1,F1);
[t_2,F_2]=Spline_3(t2,F2);
[t_3,F_3]=Spline_3(t3,F3);
[t_4,F_4]=Spline_3(t4,F4);
y_1=(1+zeros(len(t_1),1))*715;
y_2=(1+zeros(len(t_2),1))*300;
y_3=(1+zeros(len(t_3),1))*345;
y_4=(1+zeros(len(t_4),1))*175;

plot(t_1,F_1,'-b');
plot(t_2,F_2,'-r');
plot(t_3,F_3,'-k');
plot(t_4,F_4,'-c');
plot(t_1,y_1,'-b');
plot(t_2,y_2,'-r');
plot(t_3,y_3,'-k');
plot(t_4,y_4,'-c');
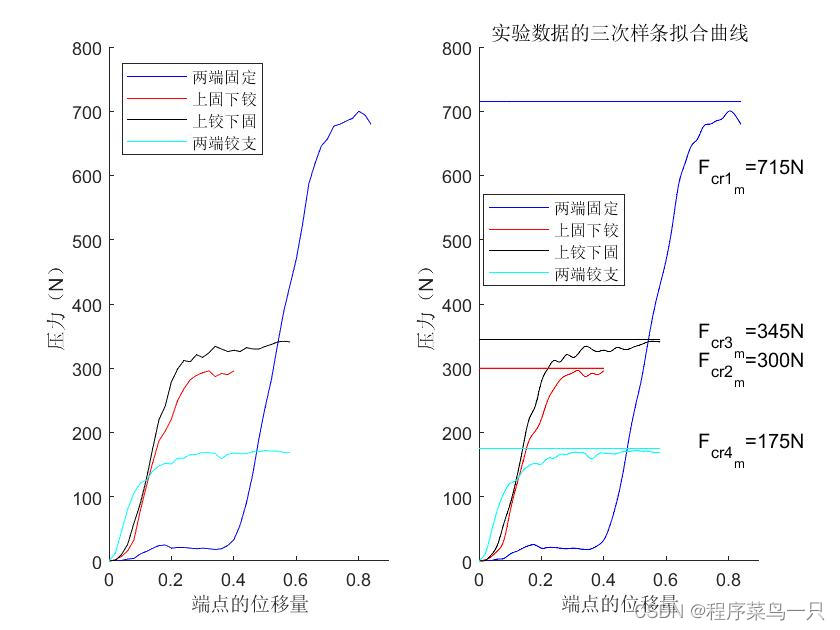
text(0.7,600,'F_{cr1_m}=715N')
text(0.7,300,'F_{cr2_m}=300N')
text(0.7,345,'F_{cr3_m}=345N')
text(0.7,175,'F_{cr4_m}=175N')
legend('两端固定','上固下铰','上铰下固','两端铰支','location','best')
xlabel('端点的位移量')
ylabel('压力（N）')
title('实验数据的三次样条拟合曲线')
axis([0,0.9,0,800])

mu=[0.5,0.7,0.7,1];
l=[0.366,0.378,0.382,0.395];
I=(1+zeros(1,4))*1.306666666667*10^-11;
E=(1+zeros(1,4))*210*10^9;
den=(mu.*l).^2;
num=pi^2*E.*I;
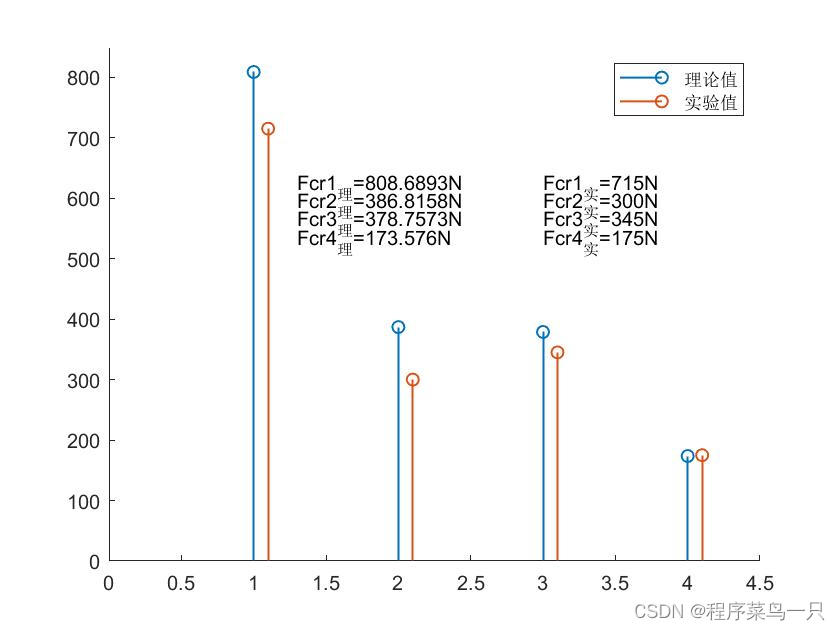
Fcr1=num./den
Fcr2=[715,300,345,175]

figure(2);
clf
x=1:1:4;
x2=1.1:1:4.1;
hold on
stem(x,Fcr1,'LineWidth',1);
stem(x2,Fcr2,'LineWidth',1);
axis([0,4.5,0,850])

for nu = 1:1:4;
    text(1.3,650-30*nu,['Fcr',num2str(nu),'_理','=',num2str(Fcr1(nu)),'N'])
    text(3,650-30*nu,['Fcr',num2str(nu),'_实','=',num2str(Fcr2(nu)),'N'])
end
legend('理论值','实验值')

四、运行结果：

五、补充

从实验的拟合效果来看，其实实验的目的是寻求一条相应的渐进线，可以看到，经过三次样条插值后，实验数据曲线更加光滑了，这也更加方便我们去估计理论中某一点的值，不过针对渐进线这一方面还是做得不够好的，读者可以发现，我的渐近线是取曲线最高点上方多一点来近似的，目前没有想到更好的方法，对拟合渐近线有见解的读者可以在评论区为我提供更好的方法

但是从结果来看，三次样条插值的结果还是很令人满意的，拟合的曲线也比较符合要求

（这也算是一个编程与实验结合的实际应用吧）