跳表

跳表是一种各方面性能都比较优秀的动态数据结构，可以支持快速的插入、删除、查找操作，写起来也不复杂，甚至可以替代红黑树（Red-black tree）。

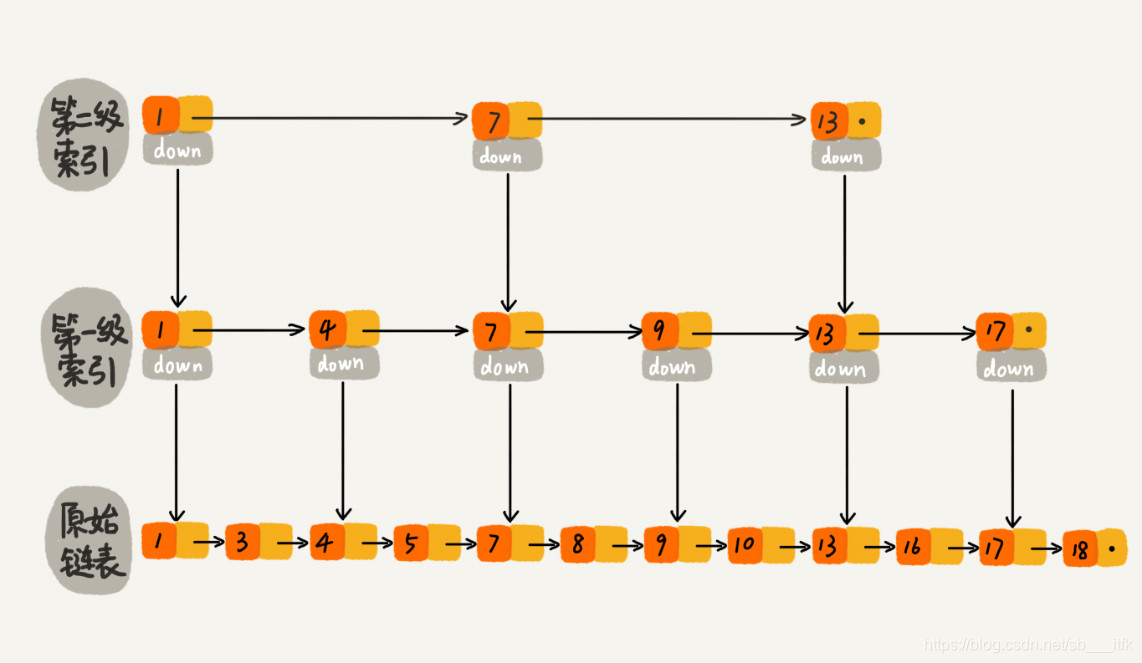有序链表加多级索引的结构就是跳表。加索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了。

跳表中查询任意数据的时间复杂度就是 O(logn)。
跳表的空间复杂度是 O(n)。

跳表这个动态数据结构，不仅支持查找操作，还支持动态的插入、删除操作，而且插入、删除操作的时间复杂度也是 O(logn)。

作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。

按照区间来查找数据这个操作，红黑树的效率没有跳表高。

const (
	//最高层数
	MAX_LEVEL = 16
)

//跳表节点结构体
type skipListNode struct {
	//跳表保存的值
	v interface{}
	//用于排序的分值
	score int
	//层高
	level int
	//每层前进指针
	forwards []*skipListNode
}

//新建跳表节点
func newSkipListNode(v interface{}, score, level int) *skipListNode {
	return &skipListNode{v: v, score: score, forwards: make([]*skipListNode, level, level), level: level}
}

//跳表结构体
type SkipList struct {
	//跳表头结点
	head *skipListNode
	//跳表当前层数
	level int
	//跳表长度
	length int
}

//实例化跳表对象
func NewSkipList() *SkipList {
	//头结点，便于操作
	head := newSkipListNode(0, math.MinInt32, MAX_LEVEL)
	return &SkipList{head, 1, 0}
}

//获取跳表长度
func (sl *SkipList) Length() int {
	return sl.length
}

//获取跳表层级
func (sl *SkipList) Level() int {
	return sl.level
}

//插入节点到跳表中
func (sl *SkipList) Insert(v interface{}, score int) int {
	if nil == v {
		return 1
	}

	//查找插入位置
	cur := sl.head
	//记录每层的路径
	update := [MAX_LEVEL]*skipListNode{}
	i := MAX_LEVEL - 1
	for ; i >= 0; i-- {
		for nil != cur.forwards[i] {
			if cur.forwards[i].v == v {
				return 2
			}
			if cur.forwards[i].score > score {
				update[i] = cur
				break
			}
			cur = cur.forwards[i]
		}
		if nil == cur.forwards[i] {
			update[i] = cur
		}
	}

	//通过随机算法获取该节点层数
	level := 1
	for i := 1; i < MAX_LEVEL; i++ {
		if rand.Int31()%7 == 1 {
			level++
		}
	}

	//创建一个新的跳表节点
	newNode := newSkipListNode(v, score, level)

	//原有节点连接
	for i := 0; i <= level-1; i++ {
		next := update[i].forwards[i]
		update[i].forwards[i] = newNode
		newNode.forwards[i] = next
	}

	//如果当前节点的层数大于之前跳表的层数
	//更新当前跳表层数
	if level > sl.level {
		sl.level = level
	}

	//更新跳表长度
	sl.length++

	return 0
}

//查找
func (sl *SkipList) Find(v interface{}, score int) *skipListNode {
	if nil == v || sl.length == 0 {
		return nil
	}

	cur := sl.head
	for i := sl.level - 1; i >= 0; i-- {
		for nil != cur.forwards[i] {
			if cur.forwards[i].score == score && cur.forwards[i].v == v {
				return cur.forwards[i]
			} else if cur.forwards[i].score > score {
				break
			}
			cur = cur.forwards[i]
		}
	}

	return nil
}

//删除节点
func (sl *SkipList) Delete(v interface{}, score int) int {
	if nil == v {
		return 1
	}

	//查找前驱节点
	cur := sl.head
	//记录前驱路径
	update := [MAX_LEVEL]*skipListNode{}
	for i := sl.level - 1; i >= 0; i-- {
		update[i] = sl.head
		for nil != cur.forwards[i] {
			if cur.forwards[i].score == score && cur.forwards[i].v == v {
				update[i] = cur
				break
			}
			cur = cur.forwards[i]
		}
	}

	cur = update[0].forwards[0]
	for i := cur.level - 1; i >= 0; i-- {
		if update[i] == sl.head && cur.forwards[i] == nil {
			sl.level = i
		}

		if nil == update[i].forwards[i] {
			update[i].forwards[i] = nil
		} else {
			update[i].forwards[i] = update[i].forwards[i].forwards[i]
		}
	}

	sl.length--

	return 0
}

func (sl *SkipList) String() string {
	return fmt.Sprintf("level:%+v, length:%+v", sl.level, sl.length)
}

以上内容摘自《数据结构与算法之美》课程，来学习更多精彩内容吧。