快速排序

快排的思想是这样的：如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。

我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

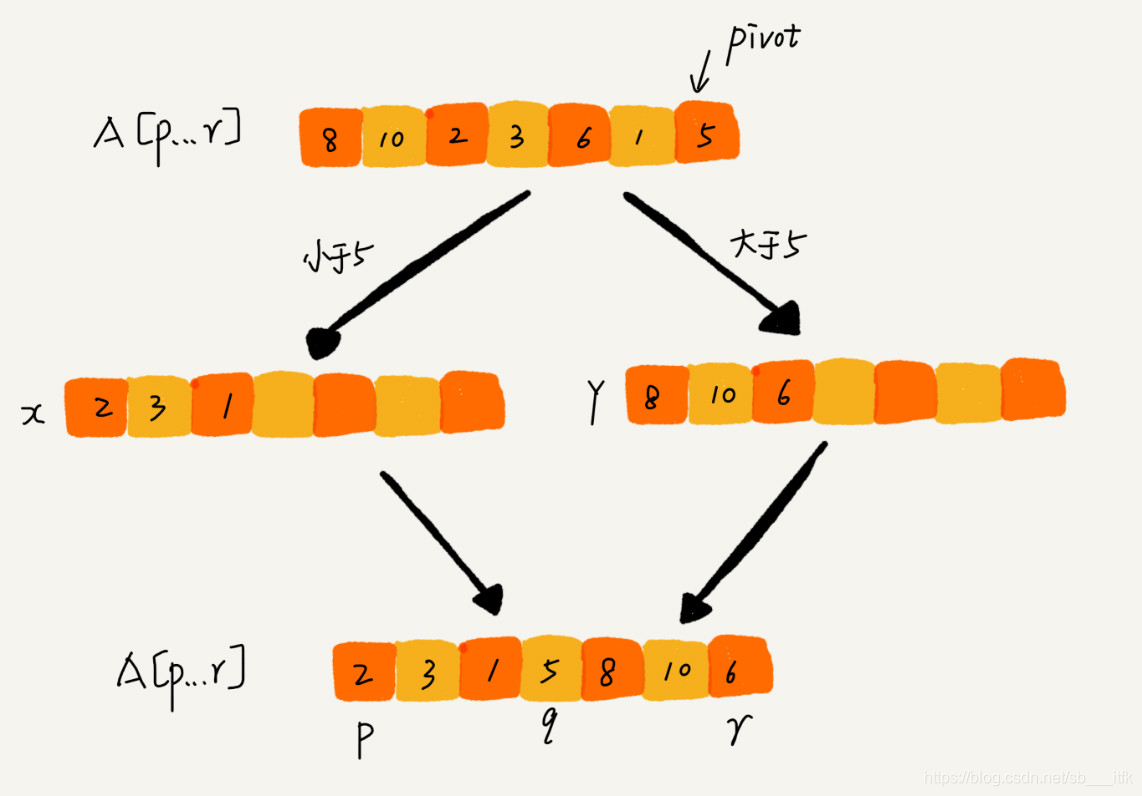根据分治、递归的处理思想，我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

如果我们用递推公式来将上面的过程写出来的话，就是这样：

递推公式：
quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)

终止条件：
p >= r

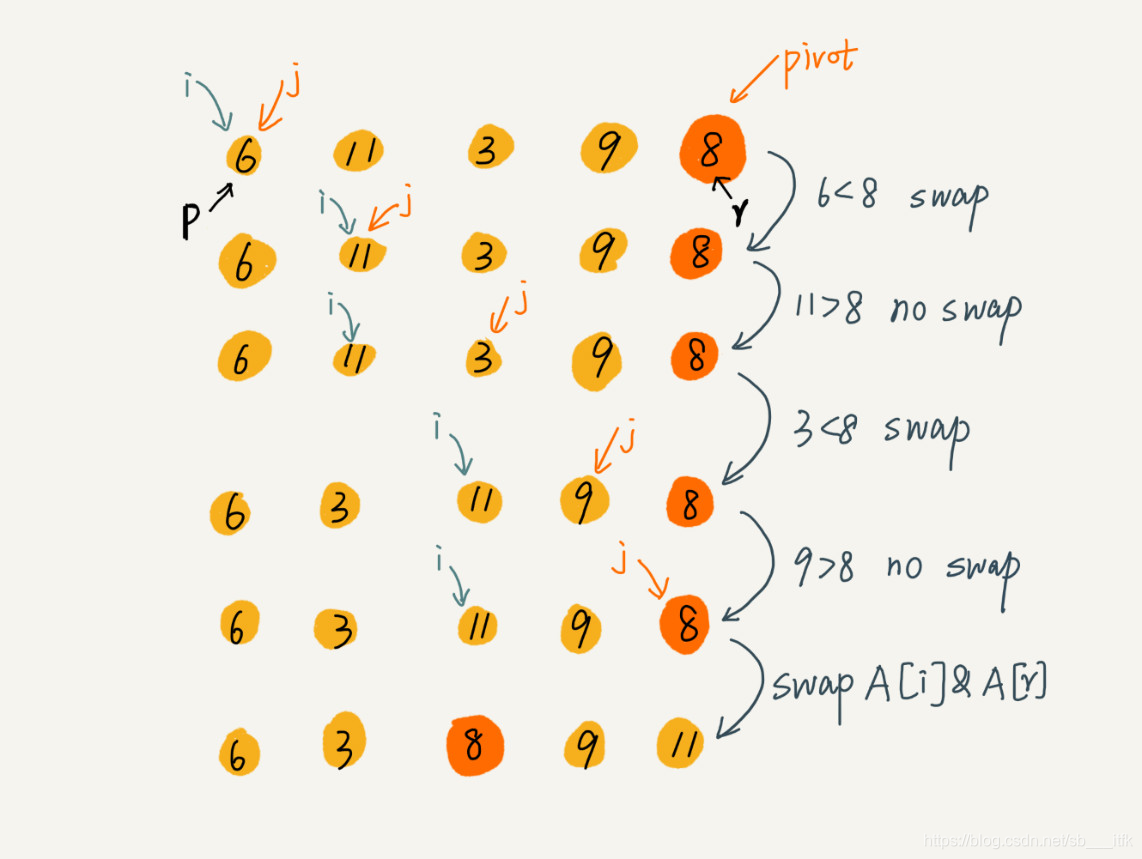
数据分组需要两个标记，i是小于pivot的分组的标记，j是遍历所有数据的标记。循环所有数据之后i之前的数据小于等于pivot，i之后（除了最后一个数据r）的数据大于pivot。最后将i和r交换，数据分组完成。
下面是代码实现

// QuickSort is quicksort methods for golang
func QuickSort(arr []int) {
	separateSort(arr, 0, len(arr)-1)
}

func separateSort(arr []int, start, end int) {
	if start >= end {
		return
	}
	i := partition(arr, start, end)
	separateSort(arr, start, i-1)
	separateSort(arr, i+1, end)
}

func partition(arr []int, start, end int) int {
	// 选取最后一位当对比数字
	pivot := arr[end]

	var i = start
	for j := start; j < end; j++ {
		if arr[j] < pivot {
			if !(i == j) {
				// 交换位置
				arr[i], arr[j] = arr[j], arr[i]
			}
			i++
		}
	}

	arr[i], arr[end] = arr[end], arr[i]

	return i
}

大部分情况下快排的时间复杂度都可以做到 O(nlogn)，只有在极端情况下，才会退化到 O(n2)。空间复杂度得是 O(1)，不是稳定的排序算法。

以上内容摘自《数据结构与算法之美》课程，来学习更多精彩内容吧。