C语言底层学习（1.二进制与原、反、补码）（超详细）

在这里开一个新的专栏

这个新专栏用来解释一些C语言相对来说更底层的东西

像是二进制码之类的东西

• 这里是say-fall分享，感兴趣欢迎互三

1. 二进制

众所周知，计算机使用的是二进制，也就是010101…
而我们数学里面计算问题用的是十进制，除此之外常用进制其实还有八进制，十六进制等。
这样的话，我们就不得不面对进制转换的问题。

1.1 二进制和十进制转换

1.1.1 十 - 二转换

整数部分：除二余一，逆序排列
什么原理呢？
其实就是一个十进制整数可以写成几个二的次方相加
以63为例：

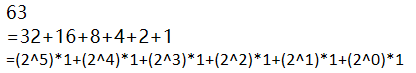
这样的话，除以2余1，就说明有2^0存在，先记录1
继续向下走，每次都会类似上面检查最后一个2^n并且记录0或1，最后再逆序输出就能得到二进制数字
小数部分：乘二取整，顺序排列
它的原理其实和整数部分一致
以0.625为例：

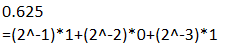
每次乘2就会顺序出现2^0,也就是小数部分第一位，记录0或1，最后再顺序输出

1.1.2 二 - 十转换

例如：111111.101
按照2的次方递增的顺序变成十进制然后全部相加，就等于63.625

1.2 二进制和八进制，十六进制转换

1.2.1 二进制转换八进制

从后往前个二进制转变为一个八进制数，不足3位的前面补0再转换

• 例如：11 111 111
  111变为7，11变为3，整体则为八进制的 377

1.2.2 二进制转换十六进制

从后往前每四个二进制转变为一个八进制数，不足4位的前面补0再转换

• 例如：111 1111 1111
  1111变成E(15)，111变为7，整体则为十六进制的 7EE

2. 原码，反码和补码

2.1 他们是什么

• 原码：先来说说原码是什么，原码其实就是在原有的二进制位前添加一个符号位，如果是正数符号位为0，负数的符号位为1.这样的话，就得到了原码
• 反码：那什么是反码呢？首先，只有负数才有反码，正数的反码与原码一致。那顾名思义，反码就是与原码“相反”的一串二进制码。注意，这里的符号位不变。
  例如：1 11111 010101
  这串二进制码的反码为1 00000 101010
• 补码：和反码一样，负数才有补码，整数的补码和原码一致。负数的补码就是在已有的反码基础上加1.

2.2 为什么要搞得这么麻烦

• 为什么要引入原码，反码和补码的概念呢，下面我来解释一下与原因：
  其实是因为计算机在处理数字的时候实际上用的都是加法，这在计算两个正数的时候的没有任何问题的，当我们计算负数

• 例如说，两个负数相加：1 010101 + 1 111111 = ？
  如果按照正常计算的话，应该等于1 1010100 也就是十进制的-84
  但是实际上，超出7位的首位就会被舍去，结果就会改变，比如说，这题的结果变为了1 010100也就是十进制的-20.

• 再举个例子，两个数做差（或者一正一负相加）：1 0101 + 0 1010 = ？
  正常计算的话，结果应该等于5(就是十进制-5和10相加)
  但是由于符号位的存在，他会把非符号位相加，符号位的正负也无法保证正确，就得到了结果 1 1111（十进制-15）

• 这样的话我们就无法在计算机上计算负数或者是做减法了吗？
  并非如此，聪明的科学家发现了一件事情，下面以十进制举例：

• -6是十进制的一个数，现在我们负号不变，只对数字本身做这样一个运算：10-6=4，我们就得到了一个4，当我们想要用1+（-6）的时候，发现结果为-5，而-5这个结果负号不变是不是等于将4和1相加再用10-5，就得到-5
  那我们就想：诶，这是不是一个巧合呀？

• 再以-7举例，做同样的操作得到一个3当我们用1+（-7）就得到一个-6，刚好就等于3和1相加（得到4）再用10-4，保留负号，就得到-6.
  经过上面这一个很绕的解释，我们回头仔细研究一下就能发现，实际上的补码就是-7为原码，-3为补码的关系
  我来画图解释一下：
  

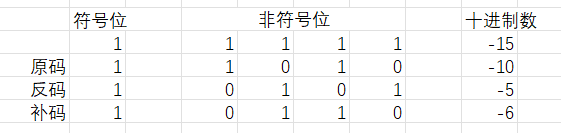
  就如同表格里一样-10和-6相加，刚好就是-16，-3和-7也是这样的关系。
  通过这样的方式，我们就能对上面不能的运算进行处理

• 这就是要引入原码，反码和补码的概念的原因。

本节完