数论-裴蜀定理、拓展欧几里得（exgcd）

最新推荐文章于 2025-11-04 14:22:31 发布

原创最新推荐文章于 2025-11-04 14:22:31 发布 · 239 阅读

0 ·

CC 4.0 BY-SA版权

数论专栏收录该内容

7 篇文章

订阅专栏

博客介绍了裴蜀定理及其在求解线性同余方程中的应用。通过使用欧几里得算法实现exgcd函数，能够找到整数解x和y，满足ax + by = gcd(a, b)。此外，还展示了如何解决模线性同余方程ax ≡ b (mod m)，当b能被最大公约数整除时给出解x的模m值。

裴蜀定理

对于任意正整数 $a$ , $b$ ,那么一定存在非零整数 $x$ , $y$ ,使得 $a x + b y = g c d (a, b)$

exgcd

推导过程：
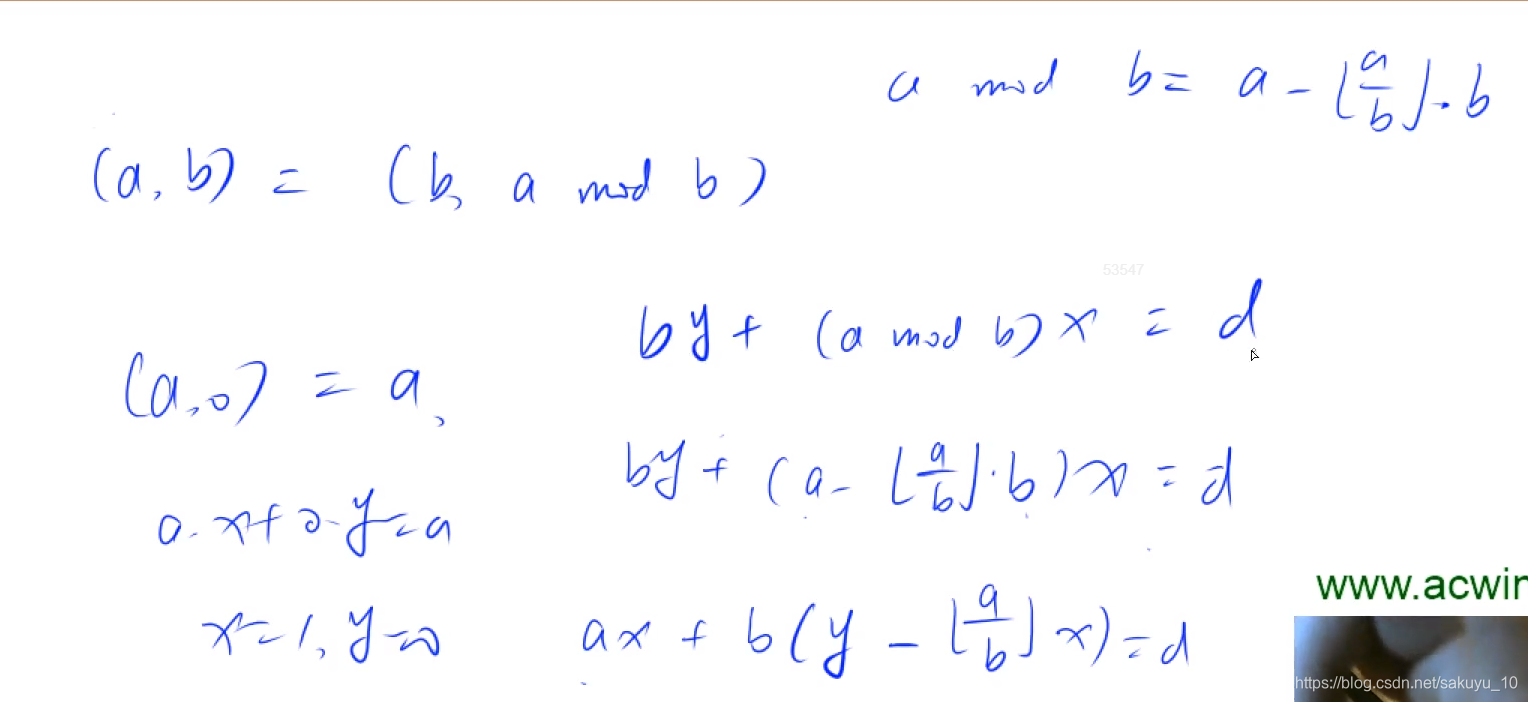
acwing

#include<bits/stdc++.h>
using namespace std;

int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1,y=0;
        return a;
    }
    
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int main(){
    int t;cin>>t;while(t--){
        int a,b,x,y;
        scanf("%d%d",&a,&b);
        
        exgcd(a,b,x,y);
        
        printf("%d %d\n",x,y);
    }
    
}

线性同余方程求解

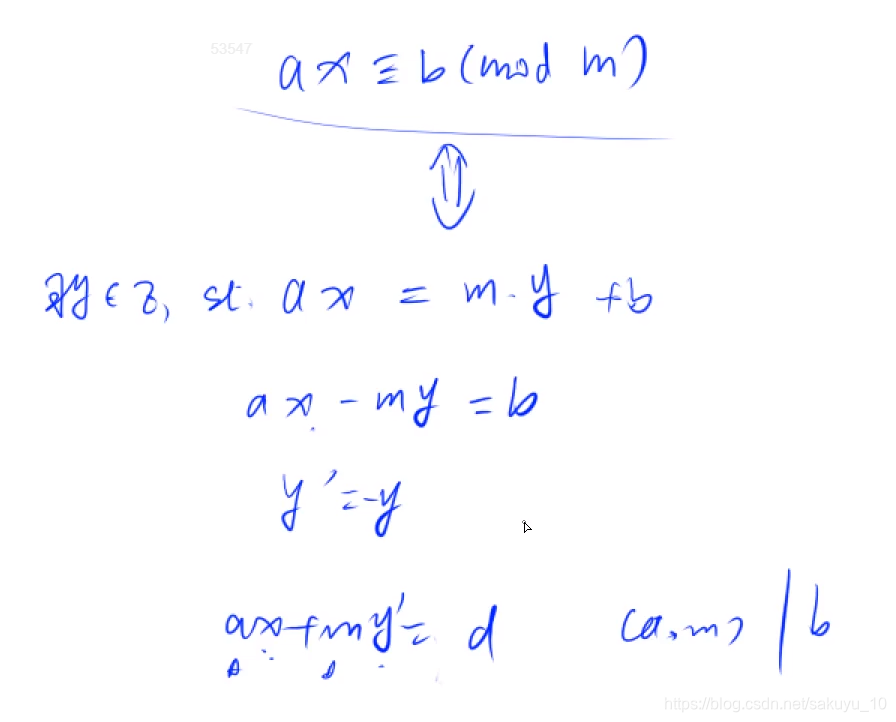
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1,y=0;
        return a;
    }
     
    int d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}
int main(){
    int t;cin>>t;while(t--){
        int a,b,m,x,y;
        scanf("%d%d%d",&a,&b,&m);
        
        int d=exgcd(a,m,x,y);
        if(b%d) cout<<"impossible"<<endl; 
        else printf("%d\n",(ll)x*(b/d)%m);
    }
    
}