机器学习算法系列（十四）-硬间隔支持向量机算法（Hard-margin Support Vector Machine）

阅读本文需要的背景知识点：拉格朗日乘子法、KKT条件、一丢丢编程知识

一、引言

  前面一节我们介绍了一种分类算法——朴素贝叶斯分类器算法，从概率分布的角度进行分类。下面我们会花几节来介绍另一种在分类问题中有着重要地位的算法——支持向量机¹ （Support Vector Machine/SVM）。
  SVM从基础到复杂可以分成三种分别为线性可分支持向量机（也就是硬间隔支持向量机）、线性支持向量机（软间隔支持向量机）、非线性支持向量机（核函数支持向量机），这一节先来介绍第一种最基础的算法——硬间隔支持向量机算法（Hard-margin Support Vector Machine）。

二、模型介绍

原始模型

  先来看下图，展示了一组线性可分的数据集，其中红点表示 -1、蓝叉表示 1 ，可以看到将该数据集分开的直线有无限多条，那么如何选择一条相对合适的直线呢？如下图中的两条直线 A、B，直观上似乎直线 A 比直线 B 更适合作为决策边界，因为对于直线 B，离某些样本点过于近，虽然依然能正确分类样本点，但当在该样本点附近预测时，会得到完全不同的结果，似乎不符合直觉，其泛化能力更差一些，而反观直线 A，其更具有鲁棒性。

图 2-1

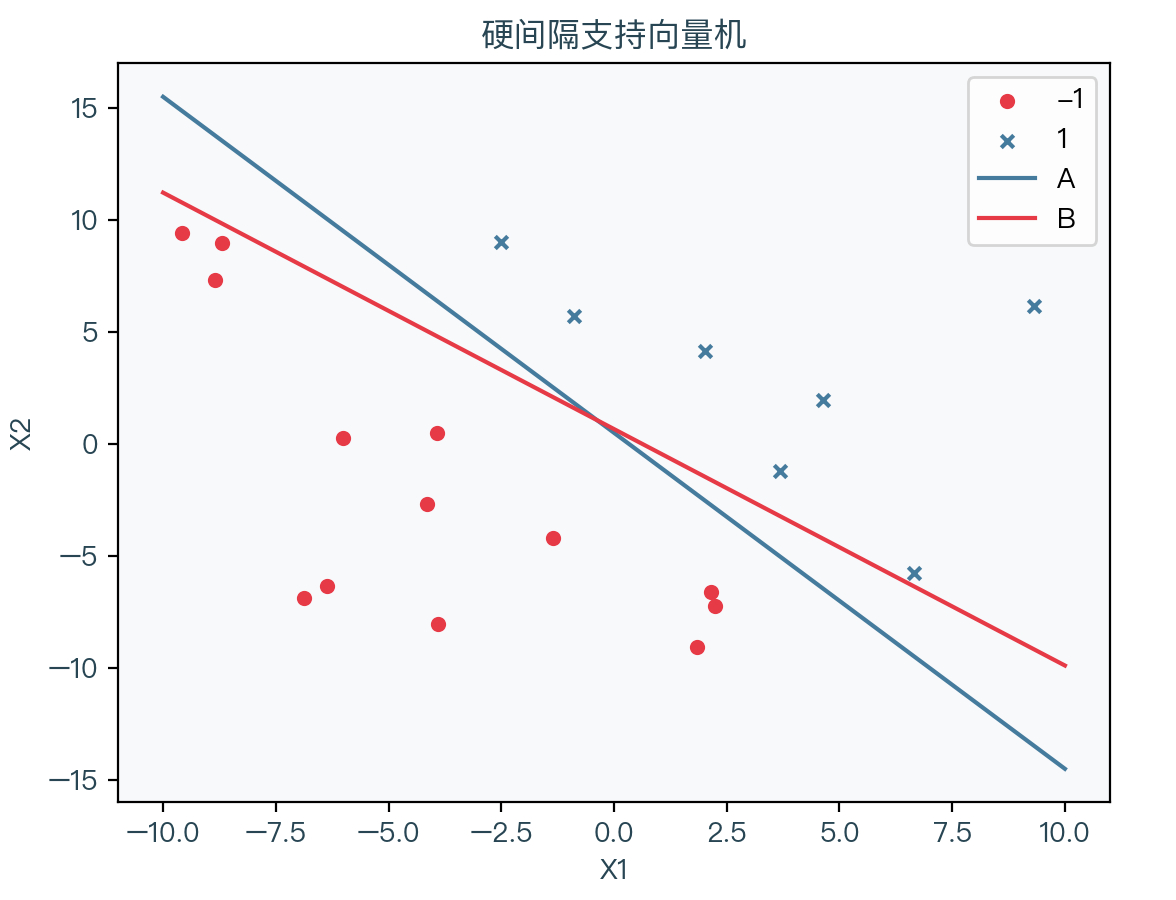
  根据上面的推断，我们的目标为找到一条直线（多维时为超平面），使得任意样本点到该超平面的距离的最小值最大。超平面表达式如下：
$$w^{T}x+b=0$$

式 2-1

  同时使得每个样本点都在正确的分类下面，即满足下式：
$$\{\begin{array}{cc}{w}^T{x}_i+b>0& y_i=+1\\ w^T{x}_i+b<0& y_i=-1\end{array}\Rightarrow y_i\left(w^T{x}_i+b\right)>0$$

式 2-2

  观察下图，可以将问题转化为找到两个超平面 A、C，使得两个超平面之间的距离最大，同时每个样本点分类正确。

图 2-2

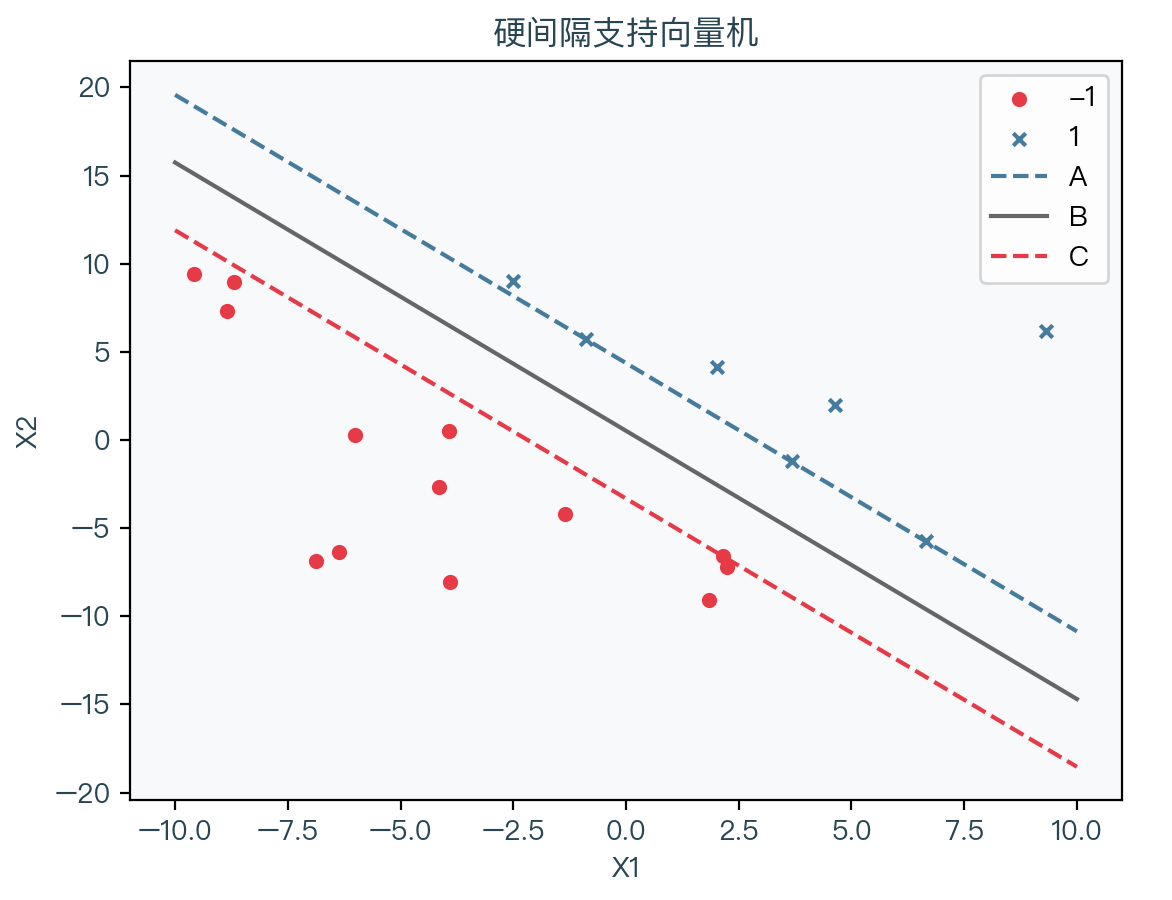
  不妨假设超平面 A 为 $wx+b=1$，超平面 B 为 $wx+b=-1$（由于 $w、b$ 都可以成比例缩放，所以必然可以找到对应的值使得上式成立），同时分类正确的条件如下：
$$\{\begin{array}{cc}{w}^T{x}_i+b\ge 1& y_i=+1\\ w^T{x}_i+b\le -1& y_i=-1\end{array}\Rightarrow y_i\left(w^T{x}_i+b\right)\ge 1$$

式 2-3

  任意一点到超平面 $wx+b=0$ 的距离为（推导见四）：
$$d=\frac{\mid w^{T}x+b\mid }{\mid w\mid }$$

式 2-4

  由上式可知超平面 A：$wx+b=1$，超平面 B：$wx+b=-1$ 之间的间距为（推导见四）：
$$\text{margin}=\frac{2}{\mid w\mid }$$

式 2-5

  那么问题转化为了如下形式：
$$\begin{array}{rl}\underset{w,b}{\max }\frac{2}{\mid w\mid }& \\ \text{ s.t. }{y}_i\left(w^T{x}_i+b\right)\ge 1& i=1,2,\cdots ,N\end{array}$$

式 2-6

  对向量的取模操作可以转化为向量内积的形式，同时取倒数，将最大值问题变成求最小值的问题，得到最后的模型如下：
$$\begin{array}{rl}\underset{w,b}{\min }\frac{1}{2}{w}^{T}w& \\ \text{ s.t. }{y}_i\left(w^T{x}_i+b\right)\ge 1& i=1,2,\cdots ,N\end{array}$$

式 2-7

对偶模型

  对原模型用拉格朗日乘子法转换一下：
（1）使用拉格朗日乘子法，即在后面加上 N 个拉格朗日乘子的条件，得到对应的拉格朗日函数
（2）拉格朗日函数对 $w$ 求偏导数并令其为零
（3）得到 $w$ 的解析解
（4）拉格朗日函数对 $b$ 求偏导数并令其为零
（5）得到新的条件
$$\begin{array}{rlr}L(w,b,\lambda )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i\left(1-y_i\left(w^T{x}_i+b\right)\right)& (1)\\ \frac{\partial L}{\partial w}& =w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0& (2)\\ w& =\sum _{i=1}^N{\lambda }_i{y}_i{x}_i& (3)\\ \frac{\partial L}{\partial b}& =-\sum _{i=1}^N{\lambda }_i{y}_i=0& (4)\\ \sum _{i=1}^N{\lambda }_i{y}_i& =0& (5)\end{array}$$

式 2-8

  将上面 $w、b$ 的解析解带回到拉格朗日函数：
（1）拉格朗日函数
（2）展开括号
（3）观察（2）式最后一项，必定为零，再带入 $w$ 的解析解
（4）化简整理得到
$$\begin{array}{rlr}L(w,b,\lambda )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i\left(1-y_i\left(w^T{x}_i+b\right)\right)& (1)\\ L(\lambda )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i-\sum _{i=1}^N{\lambda }_i{y}_{i}b& (2)\\ & =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j& (3)\\ & =\sum _{i=1}^N-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x}_i^T{x}_j& (4)\end{array}$$

式 2-9

（1）原始问题
（2）使用拉格朗日乘子法转换
（3）转换为对偶问题，要想使得原始问题与对偶问题等价，需要引入 KKT 条件
（4）带入拉格朗日函数
$$\begin{array}{rlr}& \underset{w,b}{\min }\frac{1}{2}{w}^{T}w\text{ s.t. }y\left(w^{T}x+b\right)\ge 1& (1)\\ \Rightarrow & \underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda )\text{ s.t. }\lambda \ge 0& (2)\\ \Rightarrow & \underset{\lambda }{\max }\underset{w,b}{\min }L(w,b,\lambda )\text{ s.t. }\lambda \ge 0& (3)\\ \Rightarrow & \underset{\lambda }{\max }L(\lambda )\text{ s.t. }\lambda \ge 0& (4)\end{array}$$

式 2-10

KKT（Karush-Kuhn-Tucker）条件²

  前面在推导原始问题的对偶问题中，使得两个问题等价的条件被称为 KKT 条件（Karush–Kuhn–Tucker conditions）。
  对偶问题需满足的 KKT 条件如下：
$$\{$$