代码随想录Day30 | 332.重新安排行程 51. N皇后 37. 解数独

332.重新安排行程

文档讲解：代码随想录
视频讲解： 带你学透回溯算法（理论篇）
状态

本题题目有几个要求

1. 从JFK开始
2. 所有机票必须用一次 且 只能用一次 去重
3. 字典序最小的路径

自己做的时候直接超时了，想法比较简单，定义了一个记录结果字符串的数组，然后用一个字符串来存储所有行程，同时为了避免一张机票被树枝上重复利用，还定义了一个used数组，其余的操作和基础回溯差不多，只不过还有一个参数是当前起飞地点的名字，用于在数组中搜寻满足这个起飞地点的航班。
整个递归函数如下

    void getTickets(vector<vector<string>>& tickets, string Name, vector<int> used)
    {
        if(count == tickets.size())
        {
            path.erase(path.size()-1);
            if(res.size() == 0)
            {
                res.push_back(path);
            }
            if(res.size() >0 && path < res[0])
            {//只存储最小的
                res.clear();
                res.push_back(path);
            }
            //cout<<res.size()<<" ";
            return;
        }
        for(int i = 0;i<tickets.size();i++)
        {
            //当不是当前Name就跳过
            if(tickets[i][0] != Name)
            {
                continue;
            }
            //已经用过就跳过
            if(used[i]==1)
            {
                continue;
            }
            used[i] = 1;
            int pathlen = path.size();
            path += tickets[i][1];
            path += ',';
            count++;
            getTickets(tickets, tickets[i][1],used);
            count--;
            path.erase(pathlen,pathlen+4);
            used[i]=0;
        }
        return ;
    }

在main函数中只需要再把res里面的字符串以“,”分割开就可以了，对于用例来说没问题，但是第11个测试时就超时了。
代码随想录中，利用map来处理排序的问题，通过建立一个哈希表unordered_map来存储机场可以与哪些机场对接，而存储对接机场因为也是一个机场集合所以使用了map<string,int>来排序并且表示了机场和该机票的使用次数。

//向下递归层数是票数
//找到从 JFK开始的机票
//所有行程 都要涉及 只能 用一次
//最小
class Solution {
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {
    if (result.size() == ticketNum + 1) {
        return true;
    }
    for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
        if (target.second > 0 ) { // 记录到达机场是否飞过了
            result.push_back(target.first);
            target.second--;
            if (backtracking(ticketNum, result)) return true;
            result.pop_back();
            target.second++;
        }
    }
    return false;
}
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        targets.clear();
        vector<string> result;
        for (const vector<string>& vec : tickets) {
            targets[vec[0]][vec[1]]++; // 记录映射关系
        }
        result.push_back("JFK"); // 起始机场
        backtracking(tickets.size(), result);
        return result;
    }
};

N皇后

文档讲解：代码随想录
视频讲解： 这就是传说中的N皇后？ 回溯算法安排！| LeetCode：51.N皇后
状态

对每一层的位置进行考虑，然后递归的深度即结果返回的时机就是处理到最后一行时，或者没有结果时。

void getSN(int n,int currow)
    {
    //当前的行数
        if(currow == n)
        {
            res.push_back(level);
            return;
        }
        //对这一行的每列进行遍历，一个遍历只能对应1个Q
        //过滤掉了行同时存在的情况
        for(int i = 0;i<n;i++)
        {
            if(isValid(currow,i,level,n))
            {
                level[currow][i] = 'Q';
                getSN(n,currow+1);
                level[currow][i] = '.';
            }
        }
        return ;
    }

判断是否合理可以参考上图

    //不满足的情况
    bool isValid(int currow, int curcol, vector<string> curlevel, int n)
    {
        //对于一个列
        for(int i = 0;i < currow;i++)
        {
            if(curlevel[i][curcol] == 'Q')
            {
                return false;
            }
        }
        //对于45度,从要插入位置向上搜索
        for(int i = currow-1 ,j = curcol+1;i>=0&&j<=n;i--,j++)
        {
            if(curlevel[i][j] == 'Q')
            {
                return false;
            }
        }
        //135
        for(int i = currow-1, j = curcol-1;i>=0&&j>=0;i--,j--)
        {
            if(curlevel[i][j] == 'Q')
            {
                return false;
            }
        }
        return true;
    }

37.解数独

文档讲解：代码随想录
视频讲解： 回溯算法二维递归？解数独不过如此！| LeetCode：37. 解数独
状态

二维回溯递归，对于每个点的判断1-9是否合理，如果合理就放入，然后递归，插入。如果递归过程中一直都是成立的，最后直接返回true。如果没有返回true那么就需要回溯，然后测试下一个数字放入是否合理。如果所有数字测试完都不合理，那么就需要返回false，说明这个数独无解。最终如果遍历完行和列都没有返回，那么说明处理成功直接返回true;

bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {        // 遍历行
        for (int j = 0; j < board[0].size(); j++) { // 遍历列
            if (board[i][j] != '.') continue;
            for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适
                if (isValid(i, j, k, board)) {
                    board[i][j] = k;                // 放置k
                    if (backtracking(board)) return true; // 如果找到合适一组立刻返回
                    board[i][j] = '.';              // 回溯，撤销k
                }
            }
            return false;                           // 9个数都试完了，都不行，那么就返回false
        }
    }
    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}

如何判断是否合理呢

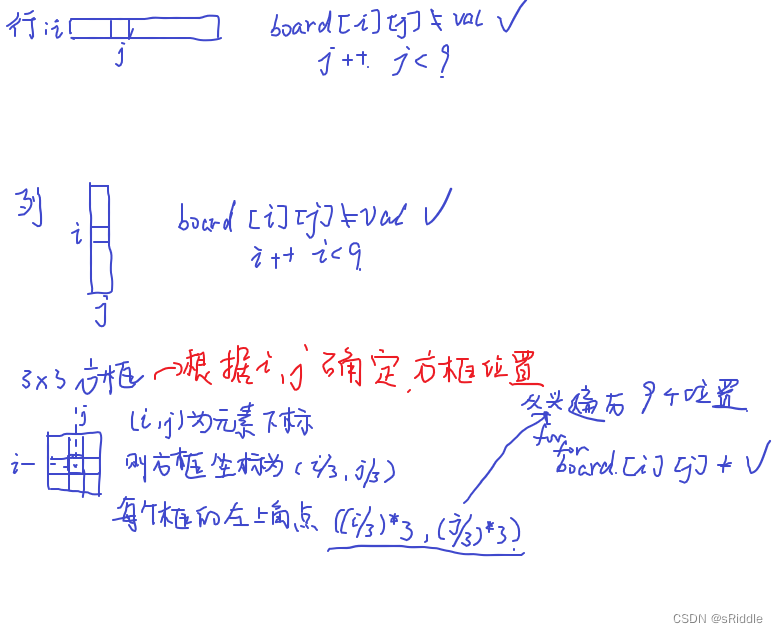
 bool isValid(vector<vector<char>>& board, int currow, int curcol,char k)
    {
        //判断行
        for(int i = 0;i<9;i++)
        {
            if(board[currow][i] == k)
            {
                return false;
            }
        }
        //判断列
        for(int i = 0;i<9;i++)
        {
            if(board[i][curcol] == k)
            {
                return false;
            }
        }
        //判断一个九宫格
        //确定currow curcol所在的九宫格起点
        int startRow = (currow/3)*3;
        int startCol = (curcol/3)*3;
        for(int i = startRow ;i<3+startRow;i++)
        {
            for(int j = startCol;j<3+startCol;j++)
            {
                if(board[i][j] == k)
                {
                    return false;
                }
            }
        }

        return true;
    }