【力扣hot100题】（048）二叉树的最近公共祖先

最新推荐文章于 2025-08-13 22:03:49 发布

回荡在随机森林的码喽

最新推荐文章于 2025-08-13 22:03:49 发布

阅读量262

点赞数 2

CC 4.0 BY-SA版权

文章标签： leetcode 算法职场和发展

本文链接：https://blog.youkuaiyun.com/s478527548/article/details/146988816

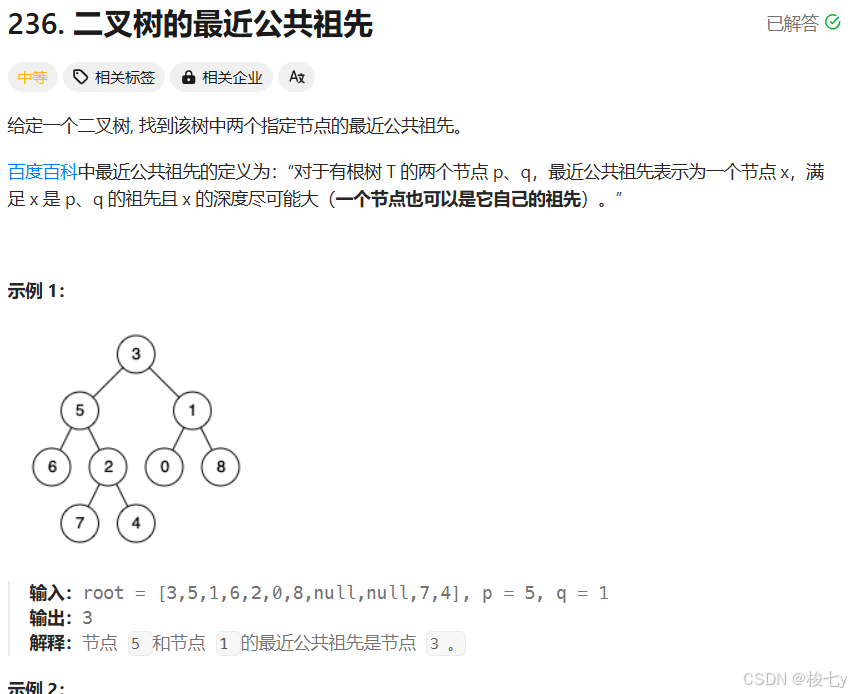
依旧只会用递归+栈。

栈记录当前遍历的节点，如果有一个节点已经被找到，则不往栈中添加新节点，并且每次回溯删除栈顶节点，每次回溯判断另一个节点有没有在栈顶节点的右边。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    stack<TreeNode*> record;
    bool search_p=0;
    bool search_q=0;
    TreeNode* result;
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root==nullptr) return result;
        if(result!=nullptr) return result;
        if(!(search_p||search_q)) record.push(root);
        if(root==p) search_p=1;
        if(root==q) search_q=1;
        if(search_p&&search_q) result=record.top();
        if(result) return result;
        lowestCommonAncestor(root->left,p,q);
        lowestCommonAncestor(root->right,p,q);
        if(record.top()==root) record.pop();
        return result;
    }
};

不过写完一提交，看着这个时空复杂度的击败比例感觉它仿佛在告诉我什么……

答案用的也是递归，不过它的时空复杂度比我的低了好多TT明明都是遍历每一个节点，为什么会变成这样………………

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
TreeNode* result;
    bool exist(TreeNode* root,TreeNode* p,TreeNode* q){
        if(root==nullptr) return 0;
        bool l=exist(root->left,p,q);
        bool r=exist(root->right,p,q);
        if((l&&r)||(root==p&&l)||(root==q&&r)||(root==p&&r)||(root==q&&l)) result=root;
        return l||r||(root==p)||(root==q);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        exist(root,p,q);
        return result;
    }
};