肌肉用力最小化与人体姿势控制

肌肉用力用于人体姿势行为的表征

埃梅尔·德米尔坎、村井昭彦、Oussama Khatib 和中村 义博

1 引言

1.1 相关工作

人类在执行常见任务时移动和协调肢体的能力非常出色。当手持重物或通过工具对环境施加力时，熟练的人类会调整其手臂和身体的姿势以最有效的方式完成任务。数学模型已被证明是运动控制预测[1, 2]和预测运动学冗余身体运动的有价值工具[3]。这些模型通常表征肌肉骨骼用力的某些方面。基于机器人学的用力模型[4]通常使用仅从骨骼运动学中推导出的量，而这些量并不特定于肌肉驱动及其动力学。因此，考虑一种类似指标来编码关于整体肌肉骨骼系统的信息，以涵盖肌肉驱动及其冗余性，是有用的。激活代表了肌肉的标准化用力，为构建此类指标提供了一个自然的起点。肌肉激活向量的幅值已在静态和动态优化中被用作优化准则[5]。

1.2 动机

最近，我们在人体运动分析方面的研究已实现了基于机器人学的人体运动合成[6]。我们的假设是，通过利用身体的运动学特性，人类有效地运用身体的机械优势，以改善肌肉张力向任务所需力的传递。然而，这种传递的效率还受到人类肌肉驱动生理学和动力学的影响。通过调整身体构型以最大化肌肉张力向任务力的传递，人类实际上是在利用其肌肉骨骼系统的生理力学优势。

本文通过多项实验验证，研究了人体姿势行为的生理力学优势。我们推测，在习得性任务中，生理力学优势的优化实际上等同于整体最小化人体肌肉用力。通过在自然人体运动中验证这一准则，我们旨在将其用于人体和类人模型的实时姿势控制。

2 肌肉用力准则

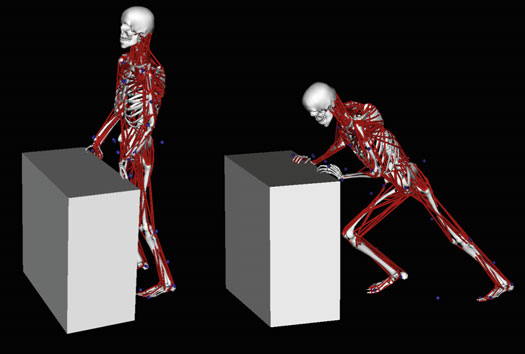
基于机器人学的用力模型通常利用仅从骨骼运动学中推导出的量，这些量并不特定于肌肉驱动和动力学。因此，考虑一种类似的度量方法来编码关于整体肌肉骨骼系统的信息，以反映肌肉驱动及其冗余性，是很有必要的。由于人体运动通常与生理能力相关联，采用一种基于模型的肌肉系统表征方法，纳入肌肉的运动学和力量特性，对于模拟人体运动至关重要。一种利用机械优势来产生姿势和任务力的策略，对应于肌肉用力最小化（图1）。在静态姿势中，肌肉产生关节力矩以抵抗重力力矩；而在动态技能中，惯性力也是用力的一部分，并被相应地考虑在内。

2.1 肌肉用力公式化

肌肉骨骼运动学为我们理解肌肉骨骼几何结构对肌肉功能的影响，以及建立肌肉力与所产生的关节力矩之间的关系提供了基础。本文定义了人体肌肉骨骼系统的肌肉雅可比矩阵，并提出了用于人体运动面向任务的表征的肌肉/任务关系。对于一个具有n个自由度和r块肌肉的人体肌肉骨骼系统，一组肌肉力m由肌肉激活a以及骨骼构型q和 ˙q决定。在此模型中，所有肌腱长度l均可由关节角度q唯一确定，其微分变化dl由以下公式给出：

$$
dl = L(q)dq. \tag{1}
$$

这里，L 是表示肌肉力臂的肌肉雅可比矩阵（图2）。肌肉诱发的关节力矩 Γ 可通过肌肉力 m 和任务力 F 之间的关系给出：

$$
\Gamma = J^T(q)F = L^T(q)m. \tag{2}
$$

为了研究肌肉用力与肌肉骨骼参数之间的关系，我们引入函数 Φ(q) 来表示包含雅可比矩阵 J(q)、肌肉雅可比矩阵 L(q)，以及肌肉发力能力 C（即最大等长收缩力）的人体肌肉骨骼系统的生理力学。生理力学优势函数 Φ(q) 定义为：

$$
\Phi = J(q)\left(L^T(q)C^2L(q)\right)^{-1}J^T(q), \tag{3}
$$

并通过雅可比矩阵将肌肉生理学与最终任务关联起来，捕捉肌肉用力测量的空间表征。

利用基于任务的用力准则的生理力学优势函数 Φ(q)，以及用于表示任务需求的广义操作空间力 F，整体用力函数可写为如下形式：

$$
E = F^T\Phi(q)F. \tag{4}
$$

2.2 与接触的动力学一致性

对于与环境的k个接触，我们通过拼接每个接触的雅可比矩阵来形成接触雅可比矩阵：

$$
J_c(q) =
\begin{bmatrix}
J_{c1} \
J_{c2} \
\vdots \
J_{ck}
\end{bmatrix}. \tag{5}
$$

类似地，对于肌肉骨骼系统要执行的m个任务，我们通过拼接每个任务的雅可比矩阵来形成任务雅可比矩阵：

$$
J_t(q) =
\begin{bmatrix}
J_{t1} \
J_{t2} \
\vdots \
J_{tm}
\end{bmatrix}. \tag{6}
$$

在存在支撑接触的情况下，我们使用任务的接触一致性雅可比矩阵，

$$
J_{t|c}(q) = J_t(q)N_c(q), \tag{7}
$$

如[8]中所定义以及与 J_c(q) 相关的动力学一致零空间矩阵，

$$
N_c(q) = I - \bar{J}_c(q)J_c(q), \tag{8}
$$

由[9]建立。下标 t|c 表示任务点与接触一致。雅可比矩阵的范围 J_{t|c}(q) 是与接触相一致的任务运动的瞬时空间。J_c(q) 是确保接触与任务之间动力学一致性的广义逆，该广义逆是唯一的，且由以下给出，

$$
\bar{J}_c(q) = A^{-1}_c(q)J^T_c(q)\Lambda(q), \tag{9}
$$

其中

$$
\Lambda(q) = \left(J_c(q)A^{-1}_c(q)J^T_c(q)\right)^{-1}, \tag{10}
$$

是操作空间动能矩阵 [10]。

因此，式(3)变为：

$$
\Phi = J_{t|c}(q)\left(L^T(q)C^2L(q)\right)^{-1}J^T_{t|c}(q). \tag{11}
$$

在本例中，左/右脚和左/右手分别表示接触点和任务点。任务雅可比矩阵和接触雅可比矩阵可分别表示为：

$$
J_t(q) = [J_{\text{RightHand}} \quad J_{\text{LeftHand}}], \quad J_c(q) = [J_{\text{RightFoot}} \quad J_{\text{LeftFoot}}]. \tag{12}
$$

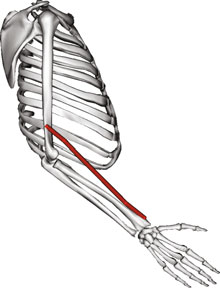（图改编自[7]))

3 肌肉骨骼模型与实验

3.1 肌肉骨骼模型

本研究所使用的肌肉骨骼模型源自上[11]和下[12]半身模型。模型的骨骼部分由刚体或骨段表示。每个身体节段均附有一个参考坐标系，该身体节段的惯性参数在此参考坐标系中表达。上半身运动学包含14个自由度（DOF），对应肩关节、肘关节、前臂、腕关节和手部。下半身运动学包含17个自由度（DOF），对应髋关节、膝关节、踝关节、距下关节和跖趾关节。手臂‐躯干、躯干‐骨盆以及骨盆‐腿关节采用球窝关节表示，其余关节为旋转关节。髋关节建模为球窝关节，膝关节建模为具有一个自由度的定制关节[13]，足部和踝关节建模为具有两个自由度的定制关节（即踝关节背屈/跖屈、跗骨外翻/内翻）。

腰椎运动建模为球窝关节[14]。肩关节建模为球窝关节，肘关节采用旋转关节建模，腕关节则采用具有三个自由度的定制关节建模（即屈伸、尺侧/桡侧偏移、旋前/旋后）。肌肉跨越关节并产生力和运动。肌肉作用线由连接至刚体的起点、止点和途经点定义。每个肌腱单元的收缩动力建模采用传统的Hill型肌肉现象学模型[15]。在我们的肌肉骨骼模型中，上肢、下肢和背部关节由118个肌腱驱动器驱动[12,14]。用于推行动作中全身用力表征的肌肉功能群如表1所示。

肩内收	肩外展
喙肱肌	三角肌
冈下肌	肩胛下肌
背阔肌	斜方肌
胸大肌
大圆肌

肩胛骨后缩	肩胛骨上提/下降
斜方肌	肩胛提肌
斜方肌	背阔肌
斜方肌	斜方肌

手臂屈曲	手臂伸展
肱二头肌	背阔肌
喙肱肌	大圆肌
胸大肌	三头肌小部

髋关节内收	髋关节外展
大收肌	臀中肌

髋关节屈曲	髋关节伸展
臀中肌	大收肌
臀中肌	股二头肌
臀中肌	臀大肌
臀中肌	半膜肌

膝关节屈曲	膝关节伸展
股二头肌	股内侧肌
半膜肌	股直肌

踝关节背屈/跖屈	踝关节外翻/内翻
趾长伸肌	趾长伸肌
拇长伸肌	腓骨短肌
腓骨第三肌	腓骨长肌
胫骨前肌/后部	腓骨第三肌
趾长屈肌	拇长伸肌
拇长屈肌	趾长屈肌
腓肠肌	拇长屈肌
腓骨短肌/长肌	胫骨前肌
比目鱼肌	胫骨后肌

躯干屈伸/旋转
腹外斜肌
腹内斜肌
竖脊肌
## 3.2 实验
对一名健康男性推一个重物进行了动作捕捉实验。要求受试者以尽可能大的力在水平方向上推该物体。每次推力试验后，要求受试者改变姿势，以便更舒适地推动物体。此过程重复了七种不同配置。受试者的动作通过八摄像头运动分析[17]系统以100赫兹的频率捕捉。地面反作用力通过两个Bertec测力台以4000赫兹的频率采集[18]。推力通过安装在物体与受试者手之间的力传感器[19]进行测量。

4 肌肉骨骼模拟与结果

4.1 用力函数的带状椭球表示

机器人学为多自由度冗余机械手的分析与控制提供了高效算法和工具。作者建立的带状椭球体[20]是一种几何表示，用于表征在末端执行器某一位置和姿态下所感知到的惯性特性。椭球体表示仅能描述有效质量（惯性）在某一方向上（或绕该方向）平方根的特性。带状椭球体则被定义为一种能够表征这些特性实际大小的几何表示。椭球体上由向量 v 表示的一点被变换为带状椭球体上由向量 w 表示的一点，其中向量 w 与 v 共线，且其大小等于 $ v^T v $[20]。

在机器人学中，带状椭球体表示[20]通过描述末端执行器运动在期望方向上的有效质量，用于评估多自由度机械手的性能。在对人体肌肉用力进行几何化描述时，带状椭球体表示可用于高效地描述在期望方向上肌肉用力的实际值，从而帮助理解为调整身体姿势或完成特定任务所需的肌肉用力。

4.2 仿真与分析结果

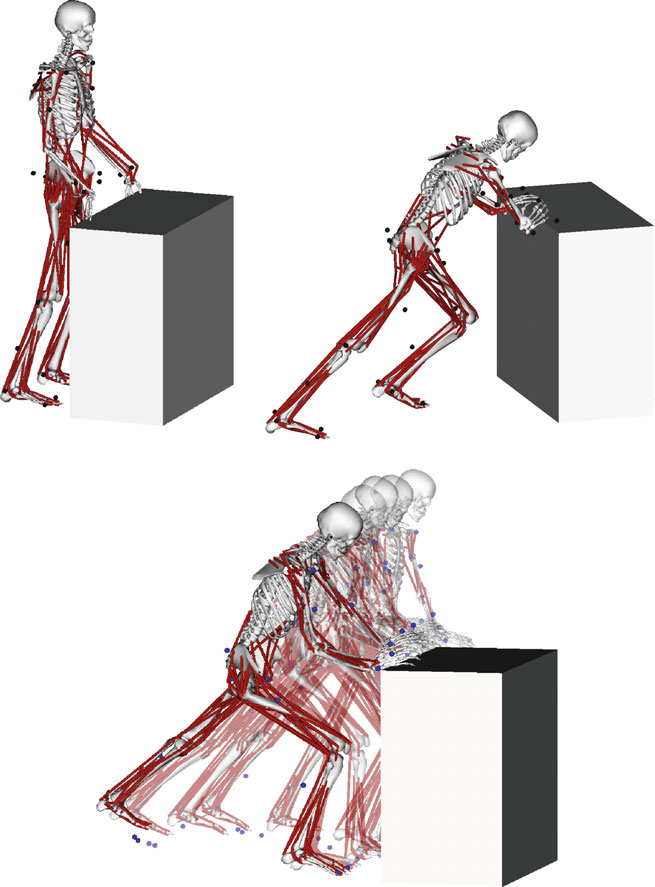
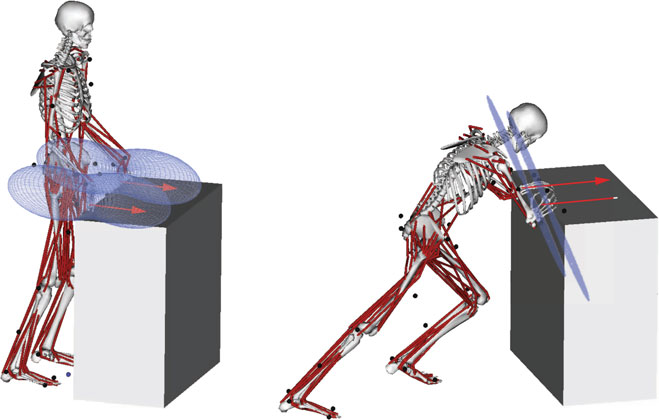
图3显示了受试者在推动物体时的两个极端姿势和五个中间姿势的三维仿真。图4展示了推动物体时采用的两种不同姿势。地面接触力 $ F_c $（用绿色箭头表示）由测力台测量，并用于计算肌肉用力。在图4中，左侧图像显示了采用不自然姿势推动物体时的肌肉骨骼模拟，以及带状椭球体（蓝色）表示在左右手上反映的全身肌肉用力。力传感器测得接触点处左右手的总力为50.4牛。红色箭头表示施加力的方向 $ F $，与带状椭球体的最长半轴对齐。这表明在推力方向上全身用力达到最大。图4右侧展示了采用自然姿势推时的肌肉骨骼模拟，其中在左右手上反映了全身肌肉用力（蓝色）的带状椭球体。力传感器测得接触点处左右手的总力为379牛。红色箭头表示施加力的方向 $ F $，与带状椭球体的最短半轴对齐。这表明在推力方向上全身用力最小。在这两种推的姿势之间，推力方向（即任务方向）上的肌肉用力减少了146倍。

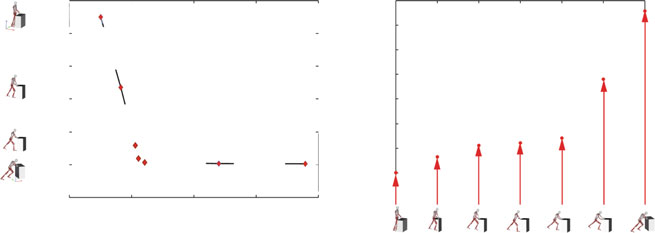
图5a 描述了七种不同配置下，全身用力在推力作用下的变化与总推力（即从左右手施加的水平力的总和）之间的关系，这些力由力传感器和测力台测量得到。图5b 描述了总推力与推力配置之间的关系。从配置一（即最大用力）到配置七（即最小用力），总推力分别为 50.4、82.6、106、111、121、239.6 和 379 牛。

随着采用更舒适的姿势，肌肉用力显著减少，最大减少了146，而作用在物体上的最大力在中间姿势时从82.6增加到239.6牛，并在最小用力的姿势下达到最大值379牛。

5 结论

一种利用生理力学优势来产生姿势和任务力的策略对应于肌肉用力的最小化。全身肌肉用力准则被用于分析多种推的姿势。在静态姿势中，肌肉产生关节力矩以抵抗重力力矩；而在动态技能中，惯性力是用力的一部分，并被相应地考虑在内。为了实现任务与接触之间的动力学一致性，计算了任务的接触一致性雅可比矩阵，并将其纳入全身肌肉用力的计算中。分析结果显示，当受试者采用更舒适的姿势推动物体时，地面反作用力和受试者体重向最终作用力的传递显著增强。这种最优传递使得全身用力减少了146，得益于骨骼构型以及肌肉运动学的优势。全身用力的最小化是与自然人体运动相关的一个准则，可用于构成控制器所期望实现的目标肌肉骨骼姿势。我们对人体肌肉用力表征的方法包括对人体测量学进行个体化缩放的肌肉骨骼模型。该方法提供个体特异性的肌肉和关节参数，如肌腱长度、力臂、作用线和关节拓扑结构。因此，该技术本质上考虑了因体型差异而导致的个体间差异。据此技术预测，不同身高体型的受试者在执行相同任务（即以最大力量推）时，会采用略有不同的关节运动学。