本文参考自: 原文地址
递归式的求解
递归式的求解主要有三种方法,分别是代入法、递归树法和主方法。递归式与分治方法紧密相连,因为使用递归式可以很自然地刻画分治算法的运行时间。换言之,对递归式进行求解有助于判断算法的优劣性,进而帮助我们选用更优的算法解决实际问题。
一、代入法求解递归式
用代入法对递归式进行求解需要分两步进行:
1. 猜测解的形式;
2. 用数学归纳法求出解中的常数,并证明解是正确的。
在猜测解的形式时,由于并不存在获得正确解的通用方法,因此这一步骤需要经验。一般而言,如果待求递归式的形式似曾相识,则猜测一个类似的解会是一种较便捷的方式。举例而言,假设已知递归式 的解为
的解为 ,那么可以假设递归式
,那么可以假设递归式 的解也为
的解也为 ,且使用代入法可证明该例子确实如此。除此之外,还有一种猜测方式是,首先证明递归式存在较为宽松的上界和下界,然后不断缩小范围。对于上述例子,可以从下界
,且使用代入法可证明该例子确实如此。除此之外,还有一种猜测方式是,首先证明递归式存在较为宽松的上界和下界,然后不断缩小范围。对于上述例子,可以从下界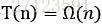 ,上界开始
,上界开始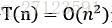 ,逐渐降低上界,提升下界,直到两者收敛,得到渐近界
,逐渐降低上界,提升下界,直到两者收敛,得到渐近界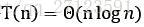 。
。
二、递归树法求解递归式
递归树法也是求解递归式的一种方法。在递归树中,每一个节点表示一个单一子问题的代价,所谓子问题即算法中的递归函数调用。对递归树的每一层求和可以得到每一层的代价;对所有层求和便可以得到总的代价。举例而言,利用递归树法求解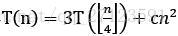 的递归式,该式对应的递归树如图1.1所示。
的递归式,该式对应的递归树如图1.1所示。
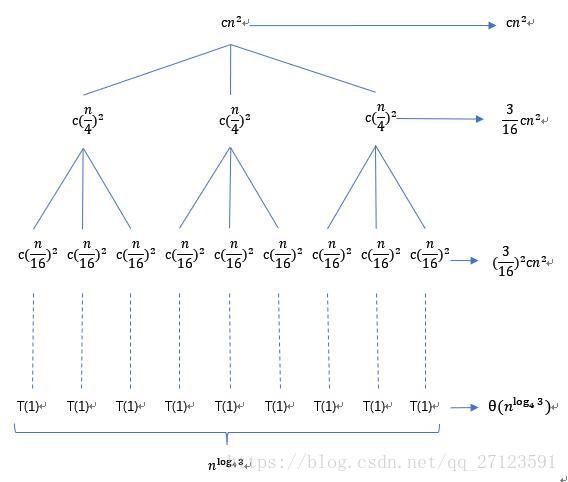
图1.1 递归式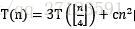 的递归树,其高度为
的递归树,其高度为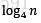 (有
(有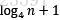 层)
层)
因为子问题的规模每一步均减少为上一步的1/4,因此最终必然会达到临界条件。由于深度为i的节点对应的子问题的规模为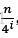 ,因此递归树的层数为
,因此递归树的层数为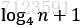 层。对于每一层的代价,当深度为i时,每一层的总代价为
层。对于每一层的代价,当深度为i时,每一层的总代价为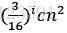 ,另外树的最底层的总代价为
,另外树的最底层的总代价为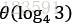 ,因此,对所有层数求和便可以得到整个递归树的总代价。
,因此,对所有层数求和便可以得到整个递归树的总代价。
根据上述思路,可以对递归树的所有层次的代价求和,来确定整棵树的代价:
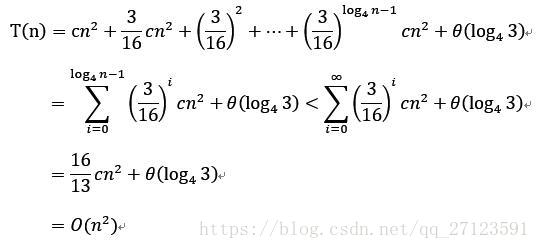
三、主方法求解递归式
用主方法求解递归式依赖定理1。
定理1:令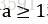 和
和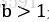 是常数,f(n)是一个函数,T(n)是定义在非负整数上的递归式:
是常数,f(n)是一个函数,T(n)是定义在非负整数上的递归式:
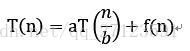
其中我们将n/b解释为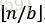 或
或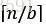 。那么T(n)有如下渐近界:
。那么T(n)有如下渐近界:
1. 若对某个常数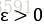 有
有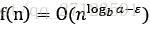 ,则
,则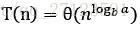 。
。
2. 若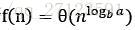 ,则
,则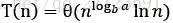 。
。
3. 若对某个常数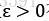 有
有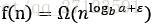 ,且对某个常数
,且对某个常数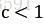 和所有足够大的n有
和所有足够大的n有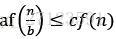 ,则
,则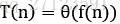 。
。








 本文详细介绍了递归式的三种求解方法:代入法、递归树法和主方法。代入法通过猜测解的形式和数学归纳法求解常数;递归树法通过构建递归树分析算法成本;主方法依赖于特定的递归形式和定理来求解。这些方法有助于理解和优化分治算法的效率。
本文详细介绍了递归式的三种求解方法:代入法、递归树法和主方法。代入法通过猜测解的形式和数学归纳法求解常数;递归树法通过构建递归树分析算法成本;主方法依赖于特定的递归形式和定理来求解。这些方法有助于理解和优化分治算法的效率。
















 4854
4854

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








