中国海洋大学OUC-数据结构-蒋若冰-第五次实验-校园导游咨询-源代码

《数据结构与算法》实验报告

实验名称	校园导游咨询
姓名		学号		日期	2024年6月5日
实验内容	设计一个校园导游程序，为来访客人提供各种信息查询服务。测试数据根据实际情况指定。提示：一般情况下，校园的道路是双向通行的，可设校园平面图是一个无向图。顶点和边均含有相关信息。
实验目的	掌握图的存储方法和最短路经算法。
实验步骤	设计西海岸校园平面图，所含Point of Interest(PoI)不少于10个。以图中顶点表示校内各PoI，存放PoI名称、代号、简介等信息；以边表示路径，存放路径长度等相关信息。（4分） 根据我对西海岸了解画出平面图，然后存储依然采用了最清晰的存储方式，邻接矩阵，但因为每个点存在明显不同，所以另设一个点的数据结构，该数据结构存储点的代号、名称和简介，边没有直接存储在邻接矩阵中，而是先以起点、终点、长度存储在数组中，然后会在创造函数中进行赋值。 点数据结构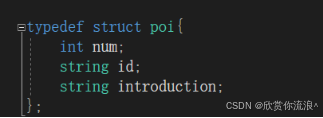： 图内容存储： 画出地图的存储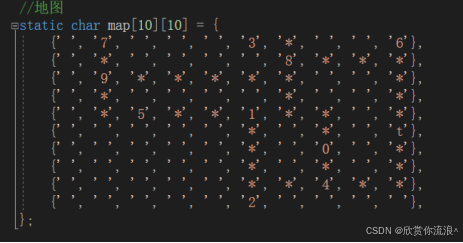： 赋值矩阵函数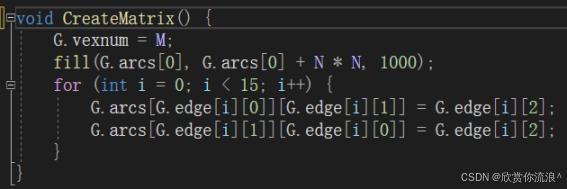： 地图信息打印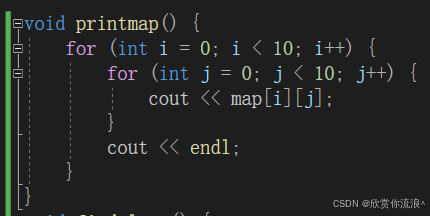： 我设计的校园平面图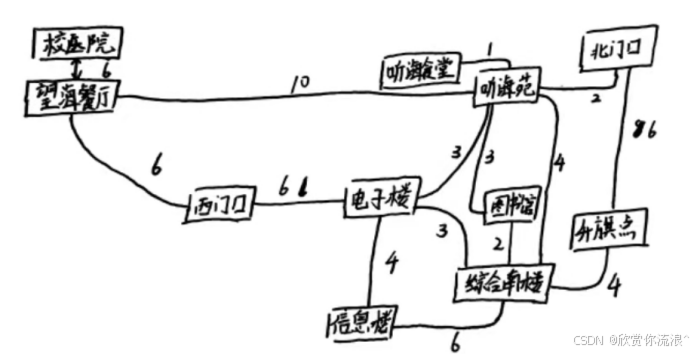： 为来访客人提供图中任意PoI相关信息的查询。（2分） 根据输入的内容，来查询对应的数组内容即可，无难度。 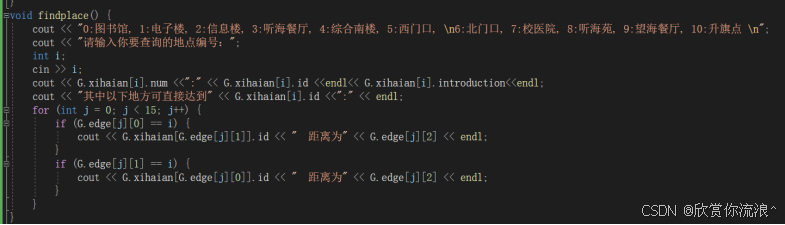为来访客人提供图中任意PoI的纹路查询，即查询任意两个PoI之间的一条最短的简单路径。（4分） 采用课程学到的迪杰斯特拉算法， 初始化辅助数组Dist：该数组用于记录从源点到图中其他所有顶点的最短路径长度。数组中的每个元素Dist[k]表示从源点到顶点k的最短路径长度。 2. Dist[k]的计算规则：Dist[k]的值可以通过以下公式计算： Min{<源点到顶点 k 的弧上的权值>，<源点到其它顶点的最短路径长度> + <其它顶点到顶点 k 的弧上的权值>}  4.初始化距离值：设置源点的距离d[0]为0，而其他所有顶点的距离d[i]初始化为无穷大（inf）。 5. 执行循环：进行n次循环，每次循环中，在所有未标记的顶点中，选择具有最小d值的顶点x，并为其添加标记。然后，对于从顶点x出发的每条边（x，y），更新顶点y的距离值d[y]，更新规则为：d[y]= min{d[y], d[x]+w(x,y)} 这里无穷我设置了10000，因为后面都会改变，所以并不重要。 算法代码：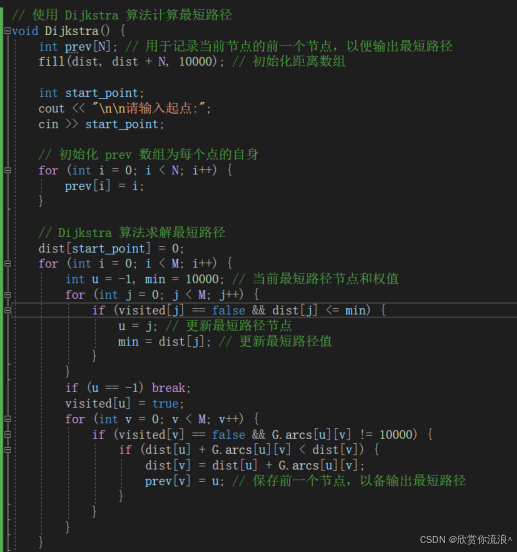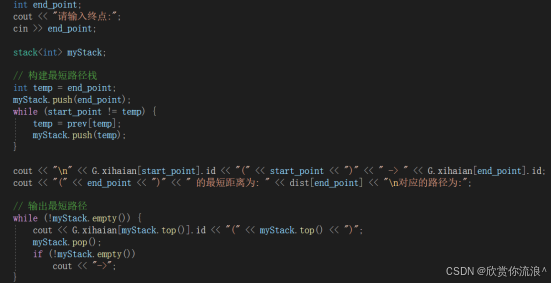
实验步骤	实验结果：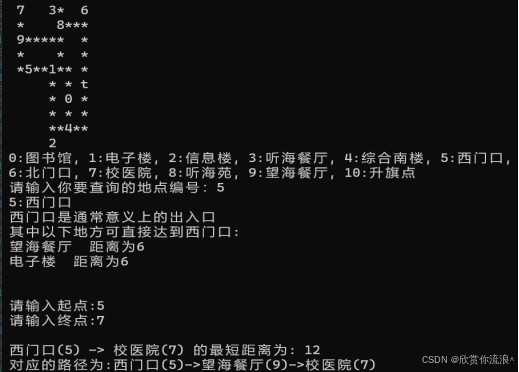
实验总结	本次实验将课堂上所讲解的迪杰斯特拉算法实现，比较偏向实际应用，首先需要自己根据西海岸的了解，来设计一个地图，同时要将这个地图打印出来。把建筑物和距离转化成“点”和“权值”的对应，然后以邻接矩阵的形式存入，去调用最短路径算法（如迪杰斯特拉算法）就可以解决问题。其次，在代码的数据结构方面，需要设计顶点的类型和图的构造，这样在查询的时候就根据存储内容，得到查询结果。最后，寻找无向图的最短路径，采用了Dijkstra算法，这与之前作业有向图最短路径的floyd算法相比，复杂度方面由O(n*n*n)优化到了O(n*n)。   这次的实验，将课堂上算法用c实现的过程，提高了我的代码能力，也将所学到的知识，应用到解决实际问题，提高了我的思维能力。

源代码：

#include <algorithm>
#include <stack>
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;

#define M 11//顶点个数
#define N 15//路径个数
#define ElemType int


typedef struct poi{
	int num;
	string id;
	string introduction;
};

typedef struct Graph {
	int arcs[M][M];//二维数组存储邻接矩阵
	int vexnum=M;//顶点数
	//点的信息
	poi xihaian[11] = { {0,"​图书馆","图书馆是学生们平时学习的地方"},{1,"电子楼","电子楼是信息工程大学部的另一栋主楼"} ,{2,"信息楼","信息楼是计算机学生做实验的地方"} ,
		{3,"听海餐厅","听海餐厅是听海居民吃饭的地方"} ,{4,"综合南楼","综合南楼是大家上课的地方"} ,{5,"西门口","西门口是通常意义上的出入口"} ,
	{6,"北门口","北门口是离宿舍很近的偷渡门"} ,{7,"校医院","能够治疗感冒等微小疾病的医院"} ,{8,"听海苑","学生们休息的地方"} ,
		{9,"望海餐厅","如果上体育课可以饱餐一顿的地方"} ,{10,"升旗点","升旗活动或自己跑步的地方"} };
	int edge[15][3] = { {7,9,6},{9,5,6},{9,8,10},{5,1,6},{3,8,1},{1,8,3},{8,6,2},{6,10,6},{4,10,4},{8,0,3},{8,4,4},{1,2,4},{1,4,3},{2,4,6},{0,4,2} };
}Graph;
Graph G;

//地图
static char map[10][10] = {
	{' ', '7', ' ', ' ', ' ', '3', '*', ' ', ' ', '6'},
	{' ', '*', ' ', ' ', ' ', ' ', '8', '*', '*', '*'},
	{' ', '9', '*', '*', '*', '*', '*', ' ', ' ', '*'},
	{' ', '*', ' ', ' ', ' ', ' ', '*', ' ', ' ', '*'},
	{' ', '*', '5', '*', '*', '1', '*', '*', ' ', '*'},
	{' ', ' ', ' ', ' ', ' ', '*', ' ', '*', ' ', 't'},
	{' ', ' ', ' ', ' ', ' ', '*', ' ', '0', ' ', '*'},
	{' ', ' ', ' ', ' ', ' ', '*', ' ', '*', ' ', '*'},
	{' ', ' ', ' ', ' ', ' ', '*', '*', '4', '*', '*'},
	{' ', ' ', ' ', ' ', ' ', '2', ' ', ' ', ' ', ' '},
};

void CreateMatrix() {
    G.vexnum = M;
	fill(G.arcs[0], G.arcs[0] + M * M, 1000);
    for (int i = 0; i < 15; i++) {
        G.arcs[G.edge[i][0]][G.edge[i][1]] = G.edge[i][2];
        G.arcs[G.edge[i][1]][G.edge[i][0]] = G.edge[i][2];
    }
}


int  weight[M], dist[M];
bool visited[M] = { false };

void printmap() {
	for (int i = 0; i < 10; i++) {
		for (int j = 0; j < 10; j++) {
			cout << map[i][j];
		}
		cout << endl;
	}
}
void findplace() {
	cout << "0:图书馆, 1:电子楼, 2:信息楼, 3:听海餐厅, 4:综合南楼, 5:西门口, \n6:北门口, 7:校医院, 8:听海苑, 9:望海餐厅, 10:升旗点 \n";
	cout << "请输入你要查询的地点编号：";
	int i;
	cin >> i;
	cout << G.xihaian[i].num <<":" << G.xihaian[i].id <<endl<< G.xihaian[i].introduction<<endl;
	cout << "其中以下地方可直接达到" << G.xihaian[i].id <<":" << endl;
	for (int j = 0; j < 15; j++) {
		if (G.edge[j][0] == i) {
			cout << G.xihaian[G.edge[j][1]].id << "  距离为" << G.edge[j][2] << endl;
		}
		if (G.edge[j][1] == i) {
			cout << G.xihaian[G.edge[j][0]].id << "  距离为" << G.edge[j][2] << endl;
		}
	}
}



// 使用 Dijkstra 算法计算最短路径
void Dijkstra() {
	int prev[M]; // 用于记录当前节点的前一个节点，以便输出最短路径
	fill(dist, dist + M, 10000); // 初始化距离数组

	int start_point;
	cout << "\n\n请输入起点:";
	cin >> start_point;

	// 初始化 prev 数组为每个点的自身
	for (int i = 0; i < M; i++) {
		prev[i] = i;
	}

	// Dijkstra 算法求解最短路径
	dist[start_point] = 0;
	for (int i = 0; i < M; i++) {
		int u = -1, min = 10000; // 当前最短路径节点和权值
		for (int j = 0; j < M; j++) {
			if (visited[j] == false && dist[j] <= min) {
				u = j; // 更新最短路径节点
				min = dist[j]; // 更新最短路径值
			}
		}
		if (u == -1) break;
		visited[u] = true;
		for (int v = 0; v < M; v++) {
			if (visited[v] == false && G.arcs[u][v] != 10000) {
				if (dist[u] + G.arcs[u][v] < dist[v]) {
					dist[v] = dist[u] + G.arcs[u][v];
					prev[v] = u; // 保存前一个节点，以备输出最短路径
				}
			}
		}
	}

	int end_point;
	cout << "请输入终点:";
	cin >> end_point;

	stack<int> myStack;

	// 构建最短路径栈
	int temp = end_point;
	myStack.push(end_point);
	while (start_point != temp) {
		temp = prev[temp];
		myStack.push(temp);
	}

	cout << "\n" << G.xihaian[start_point].id << "(" << start_point << ")" << " -> " << G.xihaian[end_point].id;
	cout << "(" << end_point << ")" << " 的最短距离为: " << dist[end_point] << "\n对应的路径为:";

	// 输出最短路径
	while (!myStack.empty()) {
		cout << G.xihaian[myStack.top()].id << "(" << myStack.top() << ")";
		myStack.pop();
		if (!myStack.empty())
			cout << "->";
	}
}


int main()
{
	CreateMatrix();
	printmap();
	findplace();
	Dijkstra();
    return 0;
}