中国海洋大学OUC-数据结构-蒋若冰-第四次实验-KMP算法的实现和应用-源代码

《数据结构与算法》实验报告

实验名称	KMP算法的实现和应用
姓名		学号		日期	2024年4月20日
实验内容	实验内容： 1.调通圆周率生成算法，生成尽可能长的圆周率序列。 2.利用自己实现的KMP算法比对圆周率序列中是否存在某个特殊序列并给出位置序号，比如本课程ID，02003048；自己的生日，YYYYMMDD。 实验要求： 1.（3分）调试正确圆周率生成函数，并生成“足够长”的圆周率序列 2.（3分）根据课程内容实现KMP模式匹配算法 3.（3分）尝试搜索匹配课程ID或8位生日序列 4.*（1分）尝试搜索匹配其他感兴趣的数字序列
实验目的	学习使用kmp算法解决问题
实验步骤	1.（3分）调试正确圆周率生成函数，并生成“足够长”的圆周率序列 采用基于Ramanujan公式的算法输出圆周率序列 圆周率的数学公式： π = 2 + 1/3 * (2 + 2/5 * (2 + 3/7 * (2 + ...  (2 + k/2k+1 * (2 + ... ))...))) 计算无限精度π，需反复运用迭代公式并保证每项精确度。但在计算机中，这几乎不可能。基本做法是多次迭代，每次迭代力求精确，直至得到PI的前n位。该程序计算了80000位，迭代公式共计280000次。（显然可以通过增加迭代次数来增加求出π的长度），程序中采用整数，分段运算出π的每几位并输出（每次计算4位）。 注释：输出语句printf("%.4d",e+d/a);中的%.4表示输出4位 π输出的实验代码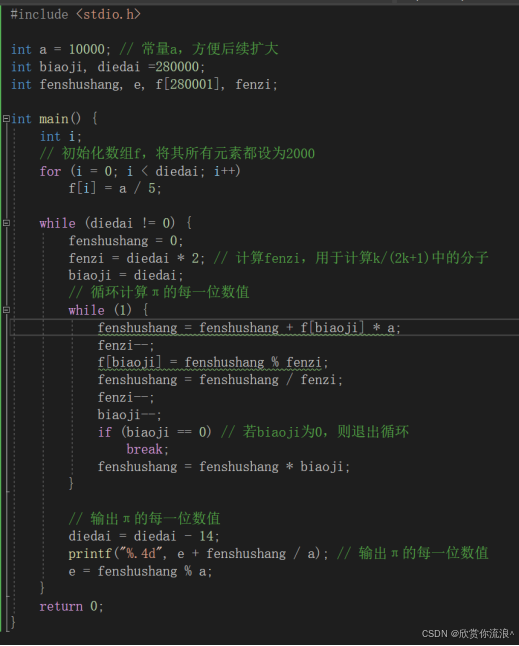： 成功输出后将π的值，编辑并存入到记事本pi.dat中，为接下来查找准备。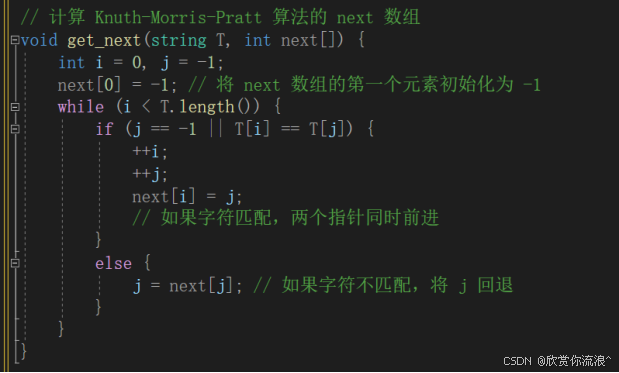 （3分）根据课程内容实现KMP模式匹配算法 优先实现next算法（已经在作业4实现过，较为轻松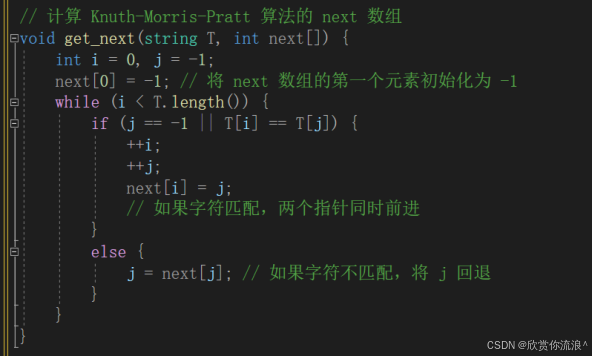）： 再实现kmp算法来查找特定字符串T： 主程序如下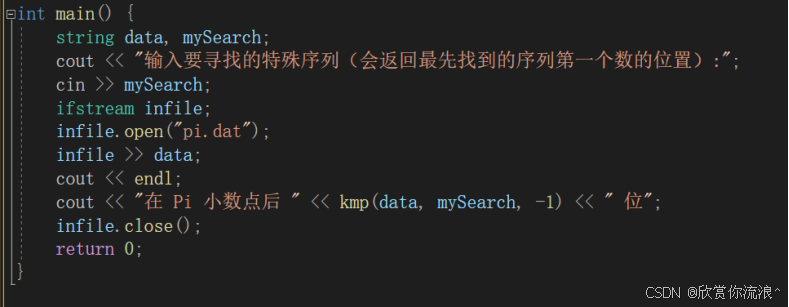： 实验结果： Pi的输出： 3.（3分）尝试搜索匹配课程ID或8位生日序列 选课号： 生日：
实验步骤	4.*（1分）尝试搜索匹配其他感兴趣的数字序列 其他的号码：
实验总结	首先是π的输出，在完成实验的过程中学习发现，π的输出算法并不止一种，除了实验中使用的Ramanujan公式（复杂度为O（n））,还有布朗开罗的连分数、反正切式、沙-波法、布丰投针等算法，在学习过程中，简单了解这些算法后，大多算法要求递归并重复利用前面的式子，以此，感受到了思路的重要性，以及考量复杂度。事实上，本次实验相较于前面几个实验较为轻松，因为之前已经在作业中实现过求next数组和kmp算法查找，在实验的第二题只需要考虑如何将输出的π放入到字符串中，如过每次都重复查找π后几千万位并记入，那么算法就过于冗余了，于是通过将实验第一题的数据储存在一个dat后缀的文件中，在程序调用时直接打开这个文件即可。在再一次学习并使用kmp算法后，我理解到强大思路带来的作用，如果直接查找那么复杂度即使是n*m，也会因为n过于庞大而使时间复杂度过高，但只要牺牲一点空间复杂度，来利用next数组，就能使时间复杂度降低到m+n。

源代码：

因π的一亿位文件占40多MB这里不再无法放入
π的输出：
#include <stdio.h>

int a = 10000; // 常量a，方便后续扩大
int biaoji, diedai =280000; 
int fenshushang, e, f[280001], fenzi;

int main() {
    int i;
    // 初始化数组f，将其所有元素都设为2000
    for (i = 0; i < diedai; i++)
        f[i] = a / 5;

    while (diedai != 0) {
        fenshushang = 0;
        fenzi = diedai * 2; // 计算fenzi，用于计算k/(2k+1)中的分子
        biaoji = diedai;
        // 循环计算π的每一位数值
        while (1) {
            fenshushang = fenshushang + f[biaoji] * a;
            fenzi--;
            f[biaoji] = fenshushang % fenzi; 
            fenshushang = fenshushang / fenzi;
            fenzi--; 
            biaoji--; 
            if (biaoji == 0) // 若biaoji为0，则退出循环
                break;
            fenshushang = fenshushang * biaoji; 
        }

        // 输出π的每一位数值
        diedai = diedai - 14;
        printf("%.4d", e + fenshushang / a); // 输出π的每一位数值
        e = fenshushang % a;
    }
    return 0;
}


Kmp查找：
#include <iostream>
#include <string>
#include <fstream>
using namespace std;

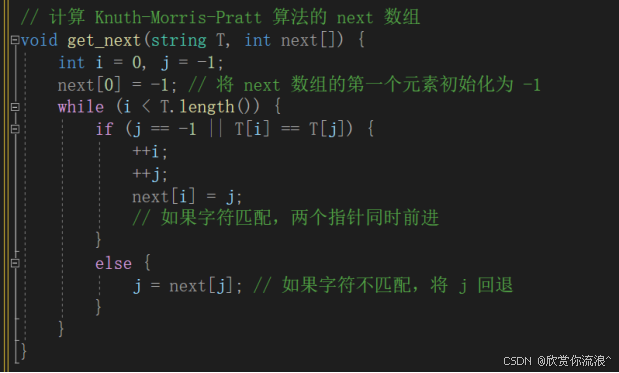
// 计算 Knuth-Morris-Pratt 算法的 next 数组
void get_next(string T, int next[]) {
    int i = 0, j = -1;
    next[0] = -1; // 将 next 数组的第一个元素初始化为 -1
    while (i < T.length()) {
        if (j == -1 || T[i] == T[j]) {
            ++i;
            ++j;
            next[i] = j;
            // 如果字符匹配，两个指针同时前进
        }
        else {
            j = next[j]; // 如果字符不匹配，将 j 回退
        }
    }
}

// 在字符串 S 中查找模式串 T 的第一个匹配位置
int kmp(string S, string T, int pos) {
    long long int i = pos, j = -1;
    int next[1000];
    get_next(T, next);
    while (i < (int)S.length() && j < (int)T.length()) {
        if (j == -1 || S[i] == T[j]) {
            ++i;
            ++j;
        }
        else {
            j = next[j];
        }
    }
    if (j == (int)T.length()) {
        return i - T.length(); // 返回匹配模式串的第一个字符的下标
    }
    else {
        return 0; // 如果未找到模式串，返回 0
    }
}

int main() {
    string data, mySearch;
    cout << "输入要寻找的特殊序列（会返回最先找到的序列第一个数的位置）:";
    cin >> mySearch;
    ifstream infile;
    infile.open("pi.dat");
    infile >> data;
    cout << endl;
    cout << "在 Pi 小数点后 " << kmp(data, mySearch, -1) << " 位";
    infile.close();
    return 0;
}