LLM 大语言模型 RoPE 相对位置编码综述

一、位置编码技术挑战

Transformer 架构的核心自注意力机制天然缺乏序列顺序感知能力，

因此位置编码成为实现语言理解的关键模块。在原始的 transformer 中

使用的是绝对位置编码，以正弦余弦编码为代表，通过固定函数生成位

置向量并叠加到词嵌入上。这个方法虽无需训练且理论支持无限外推，

但存在长序列频谱混淆问题——高频分量因周期性重复导致位置区分

度下降，低频分量则因指数衰减难以捕捉长程依赖。

当下流行使用更多的是混合编码范式，RoPE（Rotary Position

Embedding）作为新一代编码技术，通过复数空间旋转操作实现绝对位

置到相对关系的映射，成为 LLaMA、Qwen 等主流模型的核心组件。

二、传统位置编码的原理与局限

绝对位置编码：固定函数的数学困境

基本原理：Transformer 原始方案采用正弦余弦函数生成位置向量：

其中`pos`为绝对位置，`d`为嵌入维度，`i`向量索引下标。位置编码

向量是一个维度为 d 的向量和 Transformer 模型的词嵌入维度等长，

方便与词嵌入相加融合。为了用三角函数编码位置信息，将这个 d 维向

量按奇偶维度拆分：对于偶数维度（第 2i 维，i 从 0 开始取整数值 ），

用正弦函数 ( sin ) 生成编码值；对于奇数维度（第 2i + 1 维 ），用余

弦函数 ( cos ) 生成编码值。绝对位置编码的核心是给每个位置（如句子

中第 1 个、第 2 个 token）分配一个固定的向量(PE(𝑝os))。将其与词嵌入向量 (Embedding(token))相加,相当于给词向量增加了一个 “位

置偏移”，让模型能同时感知 token 的语义信息（来自词嵌入）和位置信息（来自位置编码）。

例如，第 i 个 token 的最终输入向量为：

这种加法本质是将两种信息在同

一向量空间中融合，避免了复杂的参数交互（如矩阵乘法）。该方法利

用三角函数周期性编码位置信息，理论上支持无限长度外推。

核心缺陷：

1. 语义稀释问题：位置向量通过加法注入，深层网络中位置信息易被

语义信号淹没。

2. 频谱塌缩现象：高频分量在长序列中因周期性重复出现混叠效应，

导致相邻位置难以区分。

3. 长程衰减悖论：低频分量因固定基数的指数衰减，无法有效建立跨

越大跨度位置的依赖关系。

三、RoPE 相对位置编码的原理与实现

RoPE 通过将词嵌入向量映射到复数空间，利用旋转操作编码位置信息。

具体步骤如下：

1. 复数空间映射：将词嵌入向量分解为二维子空间，每个子空间对应

一个复数分量：

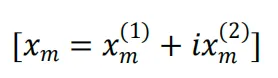
2. 旋转操作：对位置`m`的嵌入向量施加旋转矩阵：