最短路Dijkstra求最短路(讲解 + 模板 + 例题)

Dijkstra算法

Dijkstra是基于贪心思想的单源最短路算法;

变量定义 : 

const int N = 510;
const int INF = 1e9 + 10 ;
struct edge{
	int  v , w ; // 表示出边和边权 
}; 
vector<edge> e[N] ;
int d[N] ; // dis[u]存u到源点s的最短距离 
int vis[N] ;// vis[u]标记u是否出圈 
int n , m  , s ;

核心思路也就是  : 对u操作的时候 ， 有出边u->v(设边权为w),那么就可以尝试更新d[v] = min(d[v] , d[u]+w) ;

图解示例 : 

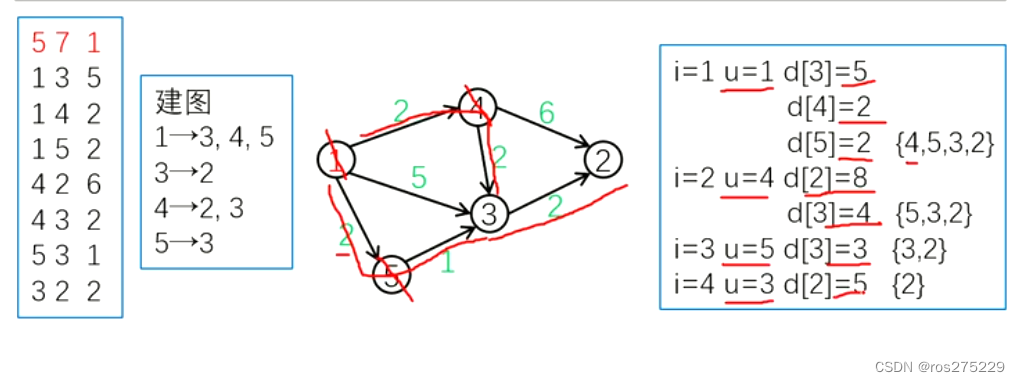
注 : 对负边权可能会出错;

模板(朴素版)  : 

时间复杂度 : O(n^2 + m) == O(n^2)

const int N =1e4 + 10;
const int INF = 1e9 + 10 ;
struct edge{
	int  v , w ; // 表示出边和边权 
}; 
vector<edge> e[N] ;
int d[N] ; // dis[u]存u到源点s的最短距离 
int vis[N] ;// vis[u]标记u是否出圈 
int n , m  , s ;

void dijkstra(int s){
    for(int i=0;i<=n;i++) d[i] = INF ;
    d[s] = 0 ;
	for(int i=1;i<n;i++){//枚举次数 
		int u = 0 ;// 相当于哨兵
		for(int j=1;j<=n;j++) 
			if(!vis[j]&&d[j]<d[u]) 
				u = j ;
 		vis[u] = 1 ;// 标记u以出圈
		for(auto ed : e[u]){// 枚举邻边 
			int v = ed.v , w = ed.w ;
			if(d[v]>d[u]+w)
				d[v] = d[u] + w ;
		}	
	}
}

堆优化版 

模拟步骤 : 

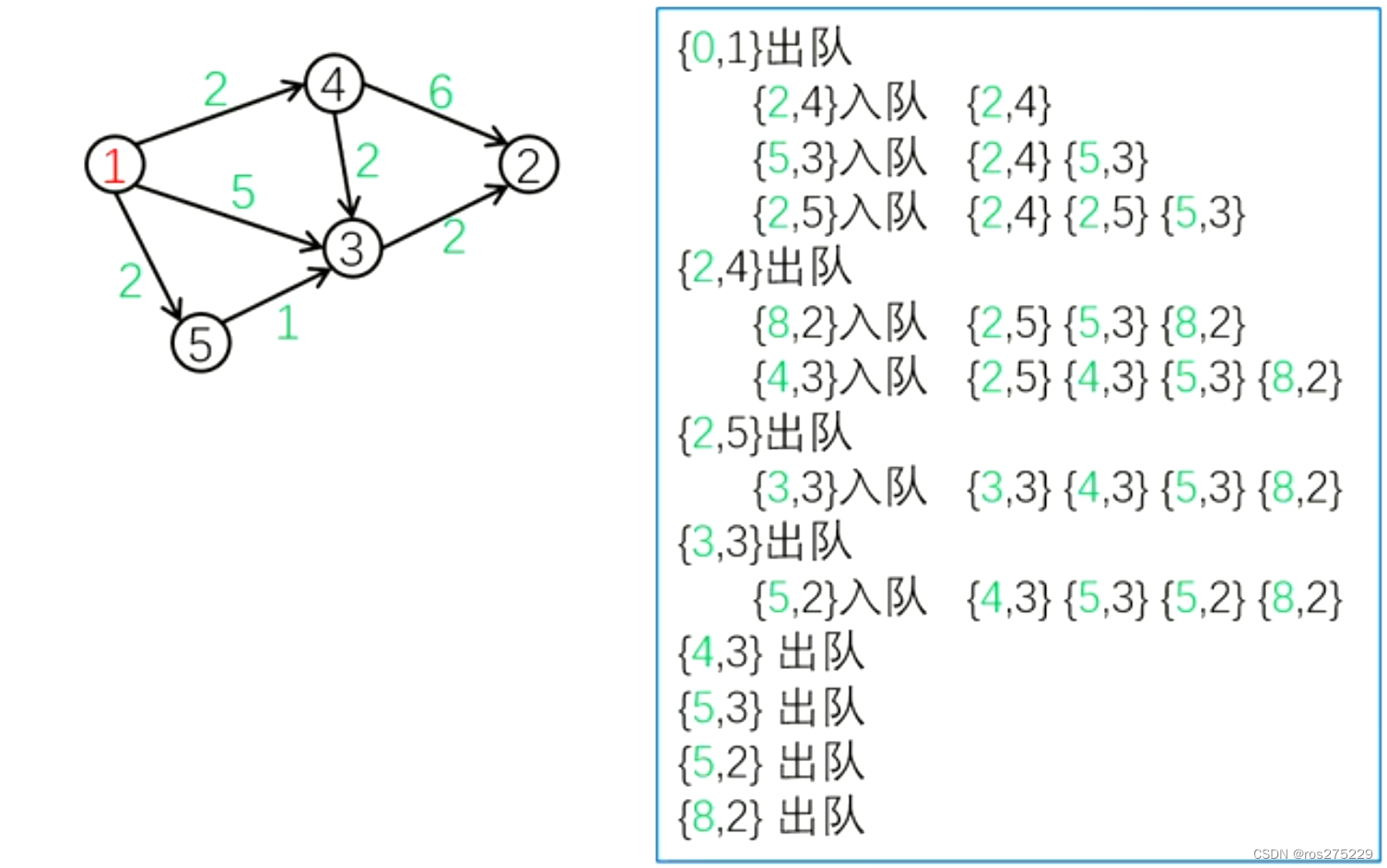
用优先队列优化找最小点的过程 : 

创建一个pair类型的大根堆q{-距离,点},把距离取负值，距离最小的元素最大，一定在堆顶 ;

1. 初始时 ， 所有点都在圈(集合)内 , vis= 0 , d[s] = 0 , d[其他点]=INF ;

2. 从队头弹出距离最小的点u,若u扩展过则跳出，否则打标记

3. 对u的所有出边执行松弛操作,把{-d[u],v}压入队尾 ;

4. 重复2,3操作，直达队列为空 ;

模板 : 

const int N =1e4 + 10;
const int INF = INT_MAX ;
typedef pair<int,int> PII ;
struct edge{
	int  v , w ; // 表示出边和边权 
}; 
vector<edge> e[N] ;
int d[N] ; // dis[u]存u到源点s的最短距离 
int vis[N] ;// vis[u]标记u是否出圈
priority_queue<PII> q ; // 距离取负 q{-距离,点} , 距离最小的元素最大，一定在堆顶 
int n , m  , s ;

void dijkstra_queue(int s){
	for(int i=0;i<=n;i++) d[i] = INF ;
	d[s] = 0 ; 
	q.push({0,s}) ;
	while(q.size()){
		auto t = q.top() ; q.pop() ;
		int u = t.second ;
		if(vis[u]) continue ;// 出过队直接跳 
		vis[u] = 1 ;// 标记u已经出队
		for(auto ed : e[u]){
			int v = ed.v  , w = ed.w ;
			if(d[v] > d[u]+w){
				d[v] = d[u] + w ;
				q.push({-d[v],v}) ;// 大根堆 
			}
		} 
	}
}

时间复杂度 : 

复杂度 : O(mlogm)

路径的记录与输出 : 

用一个pre[]数组记录前驱结点即可:

对比 : 

例题 : 

洛谷3371

【模板】单源最短路径（弱化版） - 洛谷

AC代码 : 

#include<bits/stdc++.h>
using namespace std;
const int N =1e4 + 10;
const int INF = INT_MAX ;
typedef pair<int,int> PII ;
struct edge{
	int  v , w ; // 表示出边和边权 
}; 
vector<edge> e[N] ;
int d[N] ; // dis[u]存u到源点s的最短距离 
int vis[N] ;// vis[u]标记u是否出圈
int pre[N] ;
priority_queue<PII> q ; // 距离取负 q{-距离,点} , 距离最小的元素最大，一定在堆顶 
int n , m  , s ;

void dijkstra_queue(int s){
	for(int i=0;i<=n;i++) d[i] = INF ;
	d[s] = 0 ; 
	q.push({0,s}) ;
	while(q.size()){
		auto t = q.top() ; q.pop() ;
		int u = t.second ;
		if(vis[u]) continue ;// 出过队直接跳 
		vis[u] = 1 ;// 标记u已经出队
		for(auto ed : e[u]){
			int v = ed.v  , w = ed.w ;
			if(d[v] > d[u]+w){
				d[v] = d[u] + w ;
				pre[v] = u ;
				q.push({-d[v],v}) ;// 大根堆 
			}
		} 
	}
}

void dfs_path(int u){// 递归输出路径 
	if(u==s){printf("%d ",u);return ;}
	dfs_path(pre[u]) ;
	printf("%d ",u);
}

void dijkstra(int s){
    for(int i=0;i<=n;i++) d[i] = INF ;
    d[s] = 0 ;
	for(int i=1;i<n;i++){//枚举次数 
		int u = 0 ;// 相当于哨兵
		for(int j=1;j<=n;j++) 
			if(!vis[j]&&d[j]<d[u]) 
				u = j ;
 		vis[u] = 1 ;// 标记u以出圈
		for(auto ed : e[u]){// 枚举邻边 
			int v = ed.v , w = ed.w ;
			if(d[v]>d[u]+w)
				d[v] = d[u] + w ;
		}	
	}
}


int main(){
	cin >> n >> m >> s ;
	for(int i=0;i<m;i++){
		int a , b , c ; cin >> a >> b >> c ;
		e[a].push_back({b,c});
	}
	dijkstra_queue(s) ;
	for(int i=1;i<=n;i++) cout << d[i] << " " ;
	// dfs_path(4) ;
}

洛谷4779

【模板】单源最短路径（标准版） - 洛谷

AC代码 : 

#include<bits/stdc++.h>
using namespace std;
const int N =1e5 + 10;
const int INF = INT_MAX ;
typedef pair<int,int> PII ;
struct edge{
	int  v , w ; // 表示出边和边权 
}; 
vector<edge> e[N] ;
int d[N] ; // dis[u]存u到源点s的最短距离 
int vis[N] ;// vis[u]标记u是否出圈
int pre[N] ;
priority_queue<PII> q ; // 距离取负 q{-距离,点} , 距离最小的元素最大，一定在堆顶 
int n , m  , s ;

void dijkstra_queue(int s){
	for(int i=0;i<=n;i++) d[i] = INF ;
	d[s] = 0 ; 
	q.push({0,s}) ;
	while(q.size()){
		auto t = q.top() ; q.pop() ;
		int u = t.second ;
		if(vis[u]) continue ;// 出过队直接跳 
		vis[u] = 1 ;// 标记u已经出队
		for(auto ed : e[u]){
			int v = ed.v  , w = ed.w ;
			if(d[v] > d[u]+w){
				d[v] = d[u] + w ;
				pre[v] = u ;
				q.push({-d[v],v}) ;// 大根堆 
			}
		} 
	}
}

void dfs_path(int u){// 递归输出路径 
	if(u==s){printf("%d ",u);return ;}
	dfs_path(pre[u]) ;
	printf("%d ",u);
}

void dijkstra(int s){
    for(int i=0;i<=n;i++) d[i] = INF ;
    d[s] = 0 ;
	for(int i=1;i<n;i++){//枚举次数 
		int u = 0 ;// 相当于哨兵
		for(int j=1;j<=n;j++) 
			if(!vis[j]&&d[j]<d[u]) 
				u = j ;
 		vis[u] = 1 ;// 标记u以出圈
		for(auto ed : e[u]){// 枚举邻边 
			int v = ed.v , w = ed.w ;
			if(d[v]>d[u]+w)
				d[v] = d[u] + w ;
		}	
	}
}


int main(){
	cin >> n >> m >> s ;
	for(int i=0;i<m;i++){
		int a , b , c ; cin >> a >> b >> c ;
		e[a].push_back({b,c});
	}
	dijkstra_queue(s) ;
	for(int i=1;i<=n;i++) cout << d[i] << " " ;
	// dfs_path(4) ;
}

参考 : 

D02 最短路 Dijkstra 算法_哔哩哔哩_bilibili