统计学从挂科到满分【笔记3】

第四章 专题：抽样估计

1. 抽样分布

分布：横坐标-样本值，纵坐标-出现概率
例子：某车间班组5个工人的时工资为34，38，42，46，50元，采用 重复抽样方法从5个工人中随机抽取2人构成样本。

抽取可能:

得到抽样分布图：

能计算出抽样期望：

1.1 抽样分布定理

正态分布的再生定理：
若总体符合正态分布$X_i-N(E(\bar{x}),Var(x))$，则样本均值也符合正态分布。

$Var(x)=m_{(c=2)}=\sum (x_i-\bar{x}{)}^2/n=方差=S^2=标准差的平方$
S为标准差
二阶中心动差即方差

$$Var(\bar{x})=\frac{Var(x)}{n}=\frac{S^2}{n}（重复抽样）$$
$$Var(\bar{x})=\frac{Var(x)}{n}(1-f)=\frac{S^2}{n}(1-f)（不重复抽样）$$

n为抽样数量,$Var(\bar{x})$是抽样分布的方差

例题：
某厂商产量数以亿计，声称其生产的产品具有均值为60个月，标准差为6个月的寿命分布。假设质检部门决定检验该厂的说法是否准确，为此随机抽取（不重复抽样）该厂生产的50件产品进行寿命试验。 请问：
（1）假定厂商声称是正确的，请描述50件产品的平均寿命的抽样分布；

（2）假定厂商声称是正确的，则50件产品组成的样本的平均寿命不超过57个月的概率是多少？

解：
（1）

平均寿命的均值为60月；
平均寿命的方差=$\frac{6^2}{50}$=0.72，标准差约为0.85月；
即，平均寿命服从均值60月，方差0.72的正态分布。

（2）
$$\begin{gathered} P(\bar{X}\le 57)=P(\frac{\bar{X}-60}{0.85}\le \frac{57-60}{0.85})=P(Z\le -3.529) \\ =1-P(Z\le 3.529) \\ =1-0.998=0.0002 \end{gathered}$$

2. 抽样误差

2.1 抽样标准误

抽样分布的标准差我们一般也叫抽样标准误，记作$Se(\bar{x})$

2.2 抽样极限误差

以样本统计量估计总体参数时所允许的最大误差范围 $\Delta$

概率度 $Z_{\alpha /2}$：
置信水平 $1-\alpha$
反映的是极限误差的相对程度

有公式：
$$\Delta =Z_{\alpha /2}\ast Se(\bar{x})$$

3. 区间估计

区间估计是用一个具有一定可靠程度的区间范围来估计总体参数。
区间估计的两个基本要求是置信度和精确度。
区间越大，覆盖总体参数值的可能性越高，但其精确度越低。

区间估计步骤：

• 第一步：根据样本数据计算$Se(\bar{x})$
• 第二步：给定置信水平 1-$\alpha$，计算出$Z_{a/2}$
• 第三步：计算出总体均值的估计区间$\Delta$

例题：
某企业生产某种产品的工人有1000人，某日采用不重复抽样从中随机抽取100人调查他们的当日产量。要求在95%概率保证程度下，估计该厂全部工人的人均日产量。

解：
$f_i$是各项占比，$f$是样本占总的比
第一步：计算抽样标准误差
$$\bar{x}=\frac{\sum x_i{f}_i}{\sum f_i}=\frac{116\ast 7+120\ast 18+...+140\ast 4}{100}=126件$$
$$s=\sqrt{\frac{\sum (x_i-\bar{x}{)}^2{f}_i}{\sum f_i-1}}=6.47件$$

$$Se(\bar{x})=\sqrt{\frac{s^2}{n}(1-f)}=\sqrt{\frac{6.47^2}{100}(1-\frac{100}{1000})}=0.614件$$

第二步：计算抽样极限误差

第五章 假设检验

事先对总体参数或者总体分布做出某种假设，利用样本信息来判断假设是否成立。

1. 假设验证的原理

小概率原理：
我们引入一个概念：显著性水平$\alpha$
当$\alpha \le 0.05$则我们则称之为小概率

反证法：
基于假设计算样本结果的可能性，观察显著性水平。

假设验证的步骤：
提出假设-构建验证统计量-确定拒绝域-做出决策

例子：

• 【总体】：已知去年新生婴儿的平均体重为3190g，标准差为 80。
• 【问题】：今年的新生婴儿与去年相比，体重有无显著差异？
• 【样本】：随机抽取100人，测得平均体重为3210g。

解决：

• 第一步：提出假设
  原假设：$W_{now}=W_{last}=3190g$
  备择假设：$W_{now}\ne W_{last}$
• 第二步：构建检验统计量：
  标准离差：
  （标准离差表示样本数据的离散程度）
  $$z=\frac{\bar{x}-{\mu }_0}{S/\sqrt{n}}=\frac{3210-3190}{80/\sqrt{100}}=2.5$$
• 第三步：确定拒绝域
  
  所以，有显著差异

2. 单个总体均值的检验

我们研究的问题：

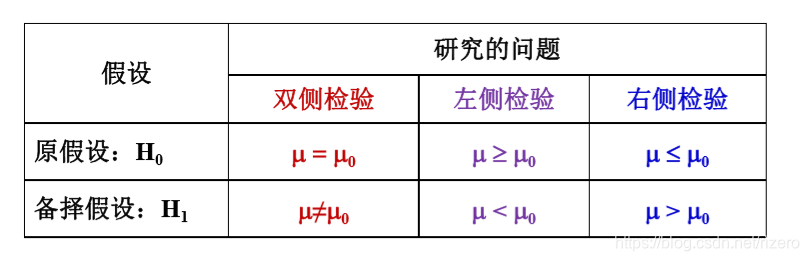
2.1 检验统计量的选择

我们一般使用标准离差作为检验统计量

例子：
某批发商欲从厂家购进一批灯泡，根据合同规定，灯泡的使用寿命平均不能低于1000小时。已知灯泡使用寿命服从正态分布，标准差为20小时。在总体中随机抽取100只灯泡， 测得样本均值为960小时。批发商是否应该购买这批灯泡？ ($\alpha$＝0.05)

解：

• 第一步：提出原假设与备择假设
  $H_0:\mu >=1000H_1:\mu <1000$
• 第二步：构建检验统计量
  $$z=\frac{960-1000}{20\sqrt{100}}=-2$$
• 第三步：确定拒绝域：
  因为$\alpha =0.05$
  
  因为z=-2，存在证据表明该批灯泡的寿命低于1000小时

3. 两个总体均值的检验

我们研究的问题：

检验统计量：
$$z=\frac{({\bar{x}}_1-{\bar{x}}_2)-({\mu }_1-{\mu }_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$$~N(0,1)

例题：
根据历史资料得知，A、B两种机器生产出的弹簧其抗拉强度的标准差分别为8公斤和10公斤。从两种机器生产的产品中各抽取一个随机样本，样本容量分别为$n_1$=32，$n_2$=40，测得两个样本的均值分别为50和44公斤。问这两种机器生产的弹簧，平均抗拉强度是否有显著差别？ ( $\alpha$= 0.05)

解：

• 第一步：提出假设与备择假设
  $H_0:{\mu }_1-{\mu }_2=0H_1:{\mu }_1-{\mu }_2\ne 0$
• 第二步：构建检验统计量
  $$z=\frac{(50-40)-0}{\sqrt{64/32+100/40}}=2.83$$
• 第三步：确定拒绝域：
  
  所以，具有显著性差异

关于 t 检验

也就是我们的检验统计量


例题:欲研究A、B两种方法组装某种产品所用的时间是否 相同。选取部分工人进行抽样分析。已知用两种工艺组装产 品所用时间服从正态分布，且$s_1$＝$s_2$ 。试问能否认为B方 法比A方法组装更好？($\alpha$= 0.05)

解：

• 第一步：提出原假设和备择假设
  $H_0:{\mu }_1-{\mu }_2\le 0H_1:{\mu }_1-{\mu }_2>0$
• 第二步：构造检验统计量
  
• 第三步：确定拒绝域