6 地球物理场波动的同步
6.1 引言
地球物理场中的随机波动携带着有关地壳内发生过程的重要信息,包括对重大地质灾害的预测。监测网络不同观测点所获取噪声测量结果的同步性,是复杂系统因其自身动力学而接近其性质发生剧烈变化的重要指标。因此,开发并测试监测数据的分析方法,以识别出相干性增强的时间段,并确定大量地球物理监测系统时间序列同步的特征频率,是一项极为紧迫的地球科学任务。本章概述了多变量时间序列的分析方法,可用于研究来自监测系统的数据流中噪声相干性变化的动力学特征。
地球物理监测的一个基本问题在于不同观测和测量的“综合化”。这一术语指的是对观测结果的联合分析不同地球物理场或同一场在不同测量点,或两者同时的观测之间的综合化。综合化的思想基于这样一种假设:利用大量监测参数有助于提取微弱的共同信号,而该信号在单独考虑各个测量时会“淹没”在强噪声中。这种共同信号的主要特征必须是在多种观测中的相干性(相关性),利用这一特性可以检测到共同成分的存在,尽管共同信号的频率成分可能与强局部噪声的频率成分重合。
识别地震或其他地质灾害的前兆是复杂测量中最具挑战性的问题之一。在这种问题中,微弱的共同信号与地震孕育过程相关,例如未来震源及其周围地壳物质的固结(’s)( Rice, 1980)。将灾难前兆的寻找视为多种观测中同步成分的出现,这是一种普遍思路,即当复杂系统因其自身动力学接近其性质的急剧变化时,该系统参数的随机波动的相关半径会增大(Gilmore, 1981; Nicolis and Prigogine, 1989)。
综合化思想需要采用多变量时间序列的分析方法。本章将介绍一套用于分析监测系统获取的多变量时间序列的算法,旨在发现不同性质和结构过程之间的隐藏关系。所开发算法的一个重要部分是对不同尺度的时间序列进行预处理分析,以提取相邻短时间间隔内的无量纲特征。这些特征被选择为无量纲形式,不依赖于原始时间序列的物理意义。这种将原始高频(HF)时间序列转换为低频(LF)序列的处理是一种重要工具,有助于检测在处理原始数据时难以发现的隐藏相干效应。此类噪声的分析常常被忽视,而噪声结构中的统计规律却是关于所研究对象即将发生的剧烈变化的重要隐藏信息来源。这些方法基于对移动时间窗内信号小波分解的典型相干性、多维谱矩阵以及典型相关系数的分析。这些算法的目的在于检测具有共同起源的极弱非平稳信号,这些信号可能表现为谐波振荡行为或强非平稳的小波特征,并识别这些共同信号出现的时间区间和频带。
6.2 基于小波的鲁棒相干性度量
基于小波的鲁棒相干性度量是对Lyubushin(2000) 和 Lyubushin 与 Kopylova (2004) 提出的多维时间序列分析方法的一种改进。在Lyubushin(2015) 的论文中,该度量被应用于全球地震噪声相干性的研究。设ZðtÞ 5ðZ1ðtÞ;…; ZqðtÞÞ T为多维度 q 的时间序列 $2,t = 0, 1, … 是一个离散时间索引,用于编号连续的样本。在长度为 N 个样本的移动时间窗口内构建了相干行为的尺度依赖性度量。假设每个时间窗口内的时间索引 t 从 0 变化到 ðN 2 1Þ。对于时间窗口的每一个位置(每次向右移动一个样本),均独立地进行分析。在对当前时间窗口中呈现的分析时间序列片段进行小波分解之前,对每个片段应用以下操作序列:
- 移除时间窗口内的总体线性趋势;
- 获得标准差的样本估计,并将每个值除以该估计值;
- 在每个时间窗口内执行加窗截断操作;
- 将窗口片段用零填充至全长 M 5 minf2m: 2m $ Ng 样本。
操作(1)消除了信号中在该时间窗口内不具有统计代表性的最强低频变化。将每个信号在窗口内除以其标准差,可对不同的时间序列进行相互调整,使其变化的总能量降低到相同的数值。第(3)点中的加窗截断操作是谱分析和小波分析中应用离散傅里叶变换或小波变换前常见的预处理步骤,其方法是将当前时间窗口内的样本乘以一个正函数,该函数在样本接近窗口左右两端时趋近于零。我们使用的是余弦截断函数,在0 ≤ t ≤ L范围内等于ð1 2 cosðπt=LÞÞ=2,在(N 2 1)L ≤ t ≤ (N 2 1)范围内等于ð1 2cosðπ(t 2(N 2 1))=LÞÞ=2。其中L表示在时间窗口起始和结束处执行加窗截断操作的时间间隔长度。我们采用的L值为5 N=8。加窗截断操作(3)对于减小有限离散小波变换的负“环绕”效应是必要的(Press等, 1996)。最后,第(4)项操作对于后续应用快速离散小波变换是必需的。
设 τ为一个宽度为N个样本的移动时间窗口右端的位置。在进行预处理操作(1)(4)后,对该时间窗口内数据进行离散正交小波变换,得到一组小波系数表:
$$
cðβ;τÞ_j ðkÞ; j = 1;…; q; k= 1;…;Mβ= 2ðm−βÞ; β= 1;…; m \quad (6.1)
$$
我们从正交小波族中选择了哈尔小波,因其最紧凑且适用于分析信号中最急剧的变化。此处 β为小波分解的细节层次数,m 是表示不小于 N 的最小整数 M 5 2m的 2 的幂。在细节层次 β上的小波系数总数量等于 Mβ= 2ðm−βÞ。索引 j 对应多维时间序列 ZðtÞ 的不同标量分量,而索引 k 依次枚举属于层次 β= 1;⋯;m 的系数。然而,其中一些系数可能对应于预处理变换第(4)步中样本的零填充。因此,在层次 β上的实际系数数量反映了该时间窗口内的信号等于 LβðNÞ= 2ðm−βÞðN=MÞ= 2−βN。每个系数 cðβ;τÞ_j ðkÞ 反映了在频带内、样本编号为 τðβÞ k= kU2β(k = 1, …, Mβ)的邻域中的信号行为,该频带的近似边界为 1⁄2ΩðβÞ min; ΩðβÞ max=1⁄21=ð2ðβ+1ÞΔsÞ; 1=ð2βΔsÞ,其中 Δs 是采样间隔的长度,从时间窗口左端位置开始测量。该邻域的宽度(即系数的时间“责任区”)等于 ΔsU2β。
随着细节层次的增加,小波系数数量呈指数级减少β。因此,LβðNÞ以相同速率递减,并从某个细节层次编号β开始,小波系数数量LβðNÞ可能等于零。因此,引入统计显著性参数Lmin是合理的,它表示在第 β个细节层次上使用小波系数进行统计估计时,小波系数数量 LβðNÞ的最小可能值。可以通过公式 βmax= max β min β :L ðNÞ$ L 确定最大可能的细节层次βmax。因此,窗口长度N和显著性阈值Lmin共同决定了可以纳入分析的小波系数的最大可能细节层次βmax。
现在我们从多变量序列Z(t)中选取一个标量时间序列j0,并构建一个度量,用于描述该序列在当前时间窗口内与其他所有标量信号之间的关系。显然,这种关系取决于所讨论的变化的尺度,因此应在不同细节层次的小波展开系数之间进行求解。为此需要解决的问题是
$$
\sum_{k=1}^{Lβ} \left| cðβ;τÞ_{j0} ðkÞ - dðβ;τÞ_{j0} ðk|γÞ \right| \to \min_γ
\quad (6.2)
$$
其中,dðβ;τÞ_{j0} ðk|γÞ 是除编号为 j0 且系数未知的信号外,所有其他标量信号在细节层次 β 上的小波系数的线性组合,其系数为 γj:
$$
dðβ;τÞ_{j0} ðk|γÞ = \sum_{j=1; j≠j0}^q γ_j U cðβ;τÞ_j ðkÞ
\quad (6.3)
$$
需要强调的是,公式(6.3)中的求和项是除选定序列j0外的时间序列展开系数的线性组合。问题(6.2)通过广义梯度方法(克拉克,1975)求解。由问题(6.2)的解得到向量 γ后,可获得dðβ;τÞ_{j0} ðk|γÞ的某些取值。现在,我们可以计算cðβ;τÞ_{j0} ðkÞ和dðβ;τÞ_{j0} ðk|γÞ在k = 1, …, Lβ 时样本值之间的相关系数;然而,在计算样本相关系数值时,我们不采用经典皮尔逊公式,而是使用其稳健修正(Huber 和 Ronchetti,2009),根据该修正,样本xðkÞ和yðkÞ(k = 1, …, n)之间的相关系数可通过以下公式计算
$$
ρðx;yÞ = \frac{S(\bar{z}
2)^2}{S(z
+^2) + S(z_-^2)}
\quad (6.4)
$$
其中
$$
\bar{z}(r) = a U x(r) + b U y(r); \quad z_-(r) = a U x(r) - b U y(r); \quad a = \frac{1}{S(x)}; \quad b = \frac{1}{S(y)}; \quad S(x) = \text{med} |x - \text{med}(x)|
\quad (6.5)
$$
其中,medðxÞ 是样本 xðkÞ 的中位数值,SðxÞ 是其绝对中位数偏差。
将xðkÞ代入cðβ;τÞ_{j0} ðkÞ,yðkÞ代入dðβ;τÞ_{j0} ðk|γÞ,n代入LβðNÞ,我们得到描述过程 j0与多变量时间序列ZðtÞ中所有其他信号之间连接程度的相 关系数的稳健值νj0ðβ; τÞ。如果在公式 (6.2) 中用其平方和代替偏差模数之和,则该问题可归结为典型相关的经典霍特林问题(霍特林,1936;拉奥,1965)。因此,此处将量νj0ðβ; τÞ称为时间序列j0的稳健典型相关。由于经典计算方法对小波系数中的异常值具有强不稳定性,因此需要用其稳健变体替代经典典型相关计算方案。这种异常值的存在源于众所周知的事实:小波分解能够在相对较少数的小波系数中累积关于信号行为的最大信息。需要强调的是,该方法在两个步骤中是稳健的:一是通过最小模法而非最小二乘法求解最小化问题 (6.2),二是通过公式 (6.4) 计算相关系数。
由于随着细节层次的增加,参与估计νkðβ; τÞ的小波系数数量呈指数下降,我们通过在先前窗口内获得的一定数量系数上引入附加平均,以减少估计中的统计波动。
$$
\nu_k(β; τ) = \frac{1}{mβ} \sum_{s=1}^{mβ} \nu_k(β; τ-s+1); \quad mβ = 2β
\quad (6.6)
$$
细节层次越高,对过去时间窗口的平均越深[式(6.6)];这一事实显著降低了估计 (6.6) 中统计涨落方差对细节层次编号的依赖性,使得不同 β值下的方差几乎相同。根据公式 (6.6),时间窗口的有效宽度变为依赖于尺度,并等于ðN + 2β - 1Þ。
我们通过公式定义基于小波的鲁棒相干性度量
$$
ρ(τ; β) = \prod_{k=1}^q |\nu_k(τ; β)|
\quad (6.7)
$$
测度 (6.7) 的值范围从 0 到 1。Eq.(6.7)的值越大,表示在相应尺度上所有分析的过程之间的总体连接越强数字 β。需要强调的是,公式(6.7)的值是 q个模小于1的非负值的乘积。因此,所分析的序列数量 q越大, ρðτ; βÞ 的绝对值就越小。因此,测度 (6.7) 的绝对值仅在序列数 q 相同时才可比较。更有意义的是测度 (6.7) 在不同 τ 取值下的相对值。因此,在使用固定的哈尔小波时,该方法有两个自由参数:时间窗口长度 N和显著性阈值 Lmin。之后我们将使用阈值 L min= 16。
应注意,公式(6.7)中的值也可以在没有对移动时间窗口内的信号进行小波分解的情况下计算。此时,它不依赖于尺度 β,并且无需使用前一时间窗内的值对[公式(6.6)]进行额外平滑。因此,分量间的鲁棒相关性ν k变得与尺度无关,而[公式(6.7)]成为鲁棒多重相关系数的公式:
$$
ρ(τ) = \prod_{k=1}^q |\nu_k(τ)|
\quad (6.8)
$$
如果 q=2,则值 [Eq.(6.8)]表示两个时间序列之间平方相关系数的稳健估计。
6.3 多重谱相干测度
多重谱相干测度类似于基于小波的多重相干,但它基于经典傅里叶基函数而非正交小波。它使用频率依赖的典型相干性,这与尺度依赖的小波基典型相关性类似。
典型相干性是当考虑两个向量时间序列时,通常的两个标量时间序列之间平方相干谱的推广:m维时间序列 XðtÞ和 n维时间序列 YðtÞ。这里 t是整数时间索引。不失一般性,假设 m#n。多个时间序列 XðtÞ和 YðtÞ之间的平方最大典型相干性 μ2ðωÞ由以下频变矩阵的最大特征值计算得出(Brillinger, 1975; Hannan,1970):
$$
U(ω) = S_{xx}^{-1} S_{xy} S_{yy}^{-1} S_{yx}
\quad (6.9)
$$
其中 ω为频率,SxxðωÞ是时间序列X(t)的m×m阶谱矩阵,SxyðωÞ是时间序列X(t)与 Y(t)之间m×n阶的互谱矩阵,SyxðωÞ= SxHy ðωÞ,H表示埃尔米特共轭(即矩阵转置与复共轭),SyyðωÞ是时间序列Y(t)的n×n阶谱矩阵。当考虑两个标量时间序列时,即m= n=1 时,使用μ2ðωÞ的值代替通常的平方相干谱。
如果我们取X(t)为q维时间序列Z(t)的第i个标量分量,Y(t)为由Z(t)所有其他标量分量组成的(q‐1)维时间序列,则函数(6.9)变为标量,可称为按分量典型相干性v2i(ω)。
值v2 iðωÞ用于衡量q维时间序列ZðtÞ的第i个标量分量在频率 ω处的变化与其他所有 ZðtÞ标量分量变化之间的关联程度。不等式0# jνiðωÞj # 1成立,且jνiðωÞj的值越接近于1,表示在频率 ω处第i个标量时间序列的变化与其余所有时间序列中相应变化之间的线性关系越强。现在,我们可以通过以下公式定义多重谱相干性测度:
$$
λ(ω) = \prod_{i=1}^q |ν_i(ω)|
\quad (6.10)
$$
值(6.10)提供了在频率处对时间序列ZðtÞ所有标量分量变化的线性联合同步性的频变度量。由于公式(6.9)中序列XðtÞ的维数等于1,m=1,因此矩阵UðωÞ实际上是一个标量。因此,其 最大特征值是以下二次型除以第i个分量功率谱的结果:
$$
ν^2_i(ω) = \frac{S_i^H(ω) (S_{ZZ}^{(i)}(ω))^{-1} S_i(ω)}{P_i(ω)}
\quad (6.11)
$$
其中 S_{ZZ}^{(i)}(ω) 是一个大小为 (q−1)×(q−1) 的厄米矩阵,它由多变量时间序列 ZðtÞ 的完整谱矩阵 SZZðωÞ(大小为 q×q)通过移除其第 i 列和第 i 行得到;Si(ω) 是一个 (q−1) 维向量,包含 ZðtÞ 的第 i 个分量与其余所有标量分量之间的互谱。显然,向量 Si(ω) 由谱矩阵 SZZðωÞ 第 i 列的元素构成,但不包括第 i 行的元素。最后 Pi(ω) 是 ZðtÞ 第 i 个分量的功率谱,即矩阵 SZZðωÞ 主对角线上的第 i 个元素。矩阵 S_{ZZ}^{(i)}(ω) 是厄米矩阵且正定 因此二次型 S_i^H(ω)(S_{ZZ}^{(i)}(ω))^{-1}Si(ω) 是实数且为正。
为了利用值(6.11)计算测度(6.10),需要估计尺寸为q ×q的谱矩阵SZZðωÞ。为此,我们使用向量自回归模型(Marple, 1987):
$$
Z(t) + \sum_{k=1}^p A_k U Z(t-k) = e(t)
\quad (6.12)
$$
其中,p 是自回归阶数,Ak 是大小为 q × q 的自回归系数矩阵,e(t) 是具有零均值和大小为 q × q 的协方差矩阵 M{e(t)eT(t)} 的 q 维残差信号。矩阵 Ak 和 Φ 通过 Durbin–Levinson 过程确定,谱矩阵通过公式计算:
$$
SZZ(ω) = F^{-1}(ω) U Φ U F^{-H}(ω); \quad F(ω) = E + \sum_{k=1}^p A_k U \exp(-iωk)
\quad (6.13)
$$
其中 E 是大小为 q ×q 的单位矩阵。
当 q = 2 时,(6.10) 的值等于通常的平方相干谱 :
$$
λ(ω) = \frac{|S_{12}(ω)|^2}{S_{11}(ω) U S_{22}(ω)}
\quad (6.14)
$$
其中 S11(ω) 和 S22(ω) 是矩阵(6.13)的对角元素,即两个信号的功率谱的参数估计,而 S12(ω) 是它们的互交叉谱。
让我们考虑移动一个特定长度的时间窗口,并设 τ为移动时间窗口右端的时间坐标。如果在每个时间窗口内独立地估计函数(6.10),那么我们将得到一个时间–频率函数:
$$
λ(τ; ω) = \prod_{i=1}^q |ν_i(τ; ω)|
\quad (6.15)
$$
值(6.15)表示多变量时间序列ZðtÞ的线性同步度量的演化。在计算谱矩阵之前,对多维时间序列的每个标量分量在每个时间窗口内独立地进行以下预处理操作,这一点非常重要。首先,消除总体线性趋势,并可选择性地进行转换为增量操作。然后,对所得数据进行缩尾处理(Huber 和 Ronchetti,2009):迭代计算样本均值和标准差σ ,将样本均值从样本中减去,然后用 σ除以各数值,所有超出 ±3σ范围的值均被替换为其极限值。迭代一直重复,直到 σ不再变化为止。这些步骤确保了相干性度量估计对异常值(极值)的稳健性。
除了频率–时间依赖性 λ(τ; ω)之外,还使用了当前时间窗口内具有坐标 τ的最大和平均相干性的纯时间依赖性度量:
$$
λ_{max}(τ) = \max_{ω_{min} ≤ ω ≤ ω_{max}} λ(τ; ω); \quad λ_{mean}(τ) = \frac{1}{m(ω_{min},ω_{max})} \sum_{ω_{min} ≤ ω ≤ ω_{max}} λ(τ; ω)
\quad (6.16)
$$
其中 m(ω_{min}; ω_{max})是频带1⁄2ω_{min}; ω_{max}内的离散频率值数量。我们注意到,量(6.16) 是 多重相关系数的某种类似物 ρ(τ),该系数由移动时间窗口中的公式 (6.8)计算得出。然而,由于公式 (6.16)中的最大值和平均值是在频率上取的,这些系数允许在当前时间窗口内考虑多维时间序列标量分量之间的时间偏移。
以公式(6.10)和 (6.11)形式表示的多重谱相干测度最初由柳布申(1998)提出,用于 地球物理监测问题中的多维时间序列处理。在后续论文(柳布申,1999,2008b,2009, 2010a,b,2014a,2016a,b;柳布申等,2003,2004;柳布申和索博列夫,2006;柳布申 和克里亚什托林,2012)中,该谱测度被应用于地球物理学、气象学、水文学和气候科学中 多维时间序列分析的不同问题。
6.4 时间片段的统计特性
为了表征在移动时间窗内分析的地球物理时间序列统计特性的变化,我们选择了三个参数:正交小波系数平方的熵En、奇异性谱支撑宽度 和广义Hurst指数Δα这两个多重分形 参数。
最小归一化熵En的平方小波系数
设X(t)为信号t=1,…,N 的有限样本,用于计数编号。归一化熵由以下公式定义:
$$
En = - \sum_{k=1}^N p_k \cdot \frac{\log(p_k)}{\log(N)}; \quad p_k = \frac{c_k^2}{\sum_{j=1}^N c_j^2}; \quad 0 ≤ En ≤ 1
\quad (6.17)
$$
其中 ck; k=1; N是通过最小化值(6.17)得到的正交小波系数。我们尝试了17种正交小波(马拉特,1998):10种常见的道布希斯小波(消失矩数量等于从1到10的整数), 以及7种所谓的对称小波(消失矩数量从4到10)。对于地球物理监测时间序列,参数En在 去除某阶多项式趋势后,在相邻的 特定长度的短时间窗口内进行估计。该操作提供了一种 将高频初始时间序列转换为其低频序列特性的可能方法。
最小归一化熵En是在 柳布申(2012) 中提出的,并被用于研究地震噪声特性,见 柳布申 (2013a,b) 和 柳布申等(2014)。该熵测度与多尺度熵具有一些共同特征,而多尺度熵是由 科斯塔等(2003, 2005) 引入用于时间序列分析的。特别是,信号的正交小波变换(如公式 (6.17) 所示)也具有多尺度性,因为它将信号分解为离散二进制时频‘原子’,其能量等于 ck2。
多重分形参数 Δα 和 α∗
设 x(t) 为一个随机信号。定义其在时间间隔 [t, t + δ] 上的变异性测度 μX(t; δ) 为最大值与最小值之差 μx(t; δ) = max_{t ≤ u ≤ t+δ} x(u) − min_{t ≤ u ≤ t+δ} x(u),并计算其平均值
$$
M(δ; q) = M[(μ_x(t; δ))^q]
$$
一个随机信号是尺度不变的(塔克,1988),如果 M(δ;q) ∝ δ^{ρ(q)}当 δ → 0 时成立,即以下极限存在:
$$
ρ(q) = \lim_{δ→0} \frac{\ln M(δ; q)}{\ln δ}
\quad (6.18)
$$
如果 ρ(q)是线性函数 ρ(q)= Hq,其中H =常数;0 , H , 1,则该过程称为单分形。当 ρ(q)是关于q的非线性凹函数时,该信号称为多重分形。为了利用有限样本x(t); t = 0,1,⋯,N−1来估计 ρ(q)的值,我们采用了一种基于去趋势波动分析(DFA)方法 (坎特尔哈特等,2002)的方法。让我们将整个时间序列划分为长度为s的不重叠区间:
$$
I_k^{(s)} = {t: 1 + (k−1)s ≤ t ≤ ks}; \quad k = 1;…; N/s
\quad (6.19)
$$
并让
$$
y_k^{(s)}(t) = x((k−1)s + t); \quad t = 1;…; s
\quad (6.20)
$$
是信号 x(t) 的一部分,对应于区间 I_k^{(s)}。设 p_k^{(s; m)}(t) 是一个阶数 m 的多项式,对信号 y_k^{(s)}(t) 进行最优拟合。考虑局部趋势偏差:
$$
Δy_k^{(s;m)}(t) = y_k^{(s)}(t) − p_k^{(s; m)}(t); \quad t = 1;…; s
\quad (6.21)
$$
并计算其值
$$
Z^{(m)}(q; s) = \left( \frac{1}{N/s} \sum_{k=1}^{[N/s]} \left( \max_{1 ≤ t ≤ s} Δy_k^{(s;m)}(t) − \min_{1 ≤ t ≤ s} Δy_k^{(s;m)}(t) \right)^q \right)^{1/q}
\quad (6.22)
$$
可以视为(M(δ_s{q}))^{1/q}的估计。定义函数h(q)为ln(Z^{(m)}(q; s))与ln(s)之间线性回归的系数:Z^{(m)}(q; s) ∝ s^{h(q)}在尺度范围s_min ≤ s ≤ s_max内拟合得到。显然, ρ(q) = qh(q),而对于单分形信号,h(q) = H = const。多重分形奇异性谱F(α)等于 Hölder–Lipschitz 指数等于 α的时间点集合t的分形维数,即满足|x(t + δ)−x(t)| ∝ |δ|^α; δ→0 的时间点集合 (费德,1988)。奇异性谱可通过标准多重分形形式进行估计,该方法包括计算吉布斯和:
$$
W(q; s) = \sum_{k=1}^{[N/s]} \left( \max_{1 ≤ t ≤ s} Δy_k^{(s;m)}(t) − \min_{1 ≤ t ≤ s} Δy_k^{(s;m)}(t) \right)^q
\quad (6.23)
$$
以及根据条件 τ(q)从 W(q; s) ∝ s^{τ(q)} 估计质量指数 (6.22) 可得 τ(q) = ρ(q)−1 = qh(q)−1。下一步,通过勒让德变换计算谱 F(α):
$$
F(α) = \max_q (αq − τ(q)); \quad 0
\quad (6.24)
$$
如果在滑动窗口中估计奇异性谱F(α),其演化可以提供有关序列“混沌”脉动结构变化的有用信息。特别是,谱F(α)的支持度的位置和宽度,即满足F(α∗) = max_α F(α)的值 α_min; α_max; Δα= α_max− α_min和 α∗,是噪声信号的特征。值α∗可称为广义赫斯特指数,它给出了最典型的利普希茨–赫尔德指数。参数 Δα(奇异性谱支撑宽度)可被视为随机行为多样性的度量。对于单分形信号,量 Δα应趋近于零且α∗= H。通常F(α∗) = 1,但也存在 F(α∗)< 1的时间窗口。最小利普希茨–赫尔德指数α_min的估计主要为正。然而,负的 α_min值 也完全可能出现(库伦蒂等人,2005;特莱斯卡等人,2005;Telesca和Lovallo,2011; Chandrasekhar等,2016),这对应于具有高幅值尖峰和阶跃特征的时间段。
在计算 Δα和α∗时,我们依据以下考虑。公式(6.23)中的指数q在区间q∈[−Q; +Q]内变化,其中Q是一个足够大的数,例如Q = 10。对于区间α∈[A_min; A_max]内的每一个试探值 α,其中A_min= min_{q∈[−Q;+Q]} dτ(q)/dq且A_max= max_{q∈[−Q;+Q]} dτ(q)/dq,我们计‐~算了F(α) = min_{q∈[−Q;+Q]}(αq − τ(q))的值。如果 α的值接近A_min,则~F(α) < 0,此值不适合作为奇异性谱的估计,因为奇异性谱必须是非负的。然而,从某个特定的 α开始,~F(α)的值变为非负,该条件定义了α_min值。随着进一步 α增大,~F(α)的值增加,在α= α∗ 时达到最大值,然后开始减小,最终在α_max < A_max处达到某一~值,使得当 α > α_max时F(α)再次变为负值。因此,条件~F(α) ≥ 0确定了奇异性谱支撑区间 α∈[α_min; α_max],其中F(α)=~F(α)。导数dτ(q)/dq是通过 τ(q)在q∈[−Q;+Q]范围内的数值计算得到的,其计算精度并不重要,因为该导数仅用于粗略确定指数q可能取值的先验区间。公式(6.22)和 (6.23)中尺度s_min的最小值选自20个样本,最大尺度等于s_max=N/5。
多重分形分析是地球物理研究中一种相当流行的工具(拉米雷斯‐罗哈斯等人,2004; 库伦蒂等人,2005;井田等人,2005;特莱斯卡等人,2005;留布申等人,2012,2014; Chandrasekhar等,2016)。在留布申等人(2012)的论文中,岩体机械监测时间序列的 多重分形分析被用于将其分割为具有不同行为特征的区间。在Lyubushin(2008b,2009, 2010a,c,2011a,b,2012,2013a,b,2014a,b)中,多重分形特性估计 Δα,α∗和 α_min 低频地震噪声被用于地震预测以及地震危险性的动态估计。
6.5 第一主成分
有必要将使用的时间序列性质序列(如(En;Δα; α∗))聚合成标量特征的时间序列,该序列 携带了初始性质集合中最常见的性质。我们在此采用了最流行的主成分方法(乔利夫, 1986)。设P(t) = (P1(t); . . . ; Pm(t))T,t = 0; 1; . . . 是一个维度为m的多变量时间序列。设 L为时间窗口内的样本数量,该时间窗口从左向右移动,最小相互位移为1,我们将此称为 “适应期”。设s为对应于移动时间窗口右端的样本编号。这意味着时间窗口包含时间索引t 满足条件s − L+1 ≤ t ≤ s的样本。让我们在对多变量时间序列分量进行归一化后,在每个 时间窗口内计算一个大小为m ×m的相关矩阵 Φ(s):
$$
Φ(s) = (ϕ_{ab}(s)); \quad ϕ_{ab}(s) = \frac{1}{L} \sum_{t=s-L+1}^s q_a^{(s)}(t) q_b^{(s)}(t); \quad a; b = 1;…; m
\quad (6.25)
$$
其中
$$
q_a^{(s)}(t) = \frac{P_a(t) - P_a^{(s)}}{σ_a^{(s)}}; \quad P_a^{(s)} = \frac{1}{L} \sum_{t=s-L+1}^s P_a(t);
$$
$$
(σ_a^{(s)})^2 = \frac{1}{L-1} \sum_{t=s-L+1}^s (P_a(t)-P_a^{(s)})^2; \quad a = 1;…; m
\quad (6.26)
$$
第一主成分 ψ(s)(t) 是通过计算得到的
$$
ψ^{(s)}(t) = \sum_{α=1}^m θ_a^{(s)} U q_a^{(s)}(t)
\quad (6.27)
$$
其中,m维向量 θ(s)=(θ_1^(s);. . . ; θ_m^(s)) T是相关性矩阵Φ(s)对应于其最大特征值的特征 向量。让我们根据以下规则,在长度为L的样本的自适应窗口内定义第一主成分的标量
6 地球物理场波动的同步
6.6 全球低频地震噪声的特性
宽频率范围内的微震振荡是地球物理研究中最常被探讨的课题之一。这归因于其可及性、大量区域和全球地震台网的存在,以及成熟的地震观测实践。即使对有关微震分析的文献进行粗略综述也显然难以完成,特别是高频微震(从0.01到100 Hz及以上,直至地震声波)的分析更是如此。高频微震观测的广泛开展得益于仪器设备的相对简单性和便携性,且无需像低频地球物理监测那样严格要求传感器的长期稳定性。在麦克纳马拉和布兰德(2004)的研究中,展示了对自然和工业起源的微震背景在0.01–16Hz频带内的详细研究成果,包括构建功率谱特性的时间(昼夜和季节)和空间分布估计器。关于短周期微震组成的更近期研究见于科珀和德福伊(2008)以及科珀等(2010)。随着所研究的微震背景振荡周期的增加,大气和海洋波作为微震主要来源的作用变得愈发显著。伯杰等(2004)综述了利用IRIS宽带地震台站研究背景微震的情况。在施特尔等(2006)中研究了周期范围为 5–40秒的微震振荡,并确认了其海洋成因。周期为 100–500秒的持续观测到的微震振荡在弗里德里希等(1998)、小林和西田(1998)、谷本(2001, 2005)以及阿尔杜安等(2011)的研究中被考察。这些振荡既由弱震产生,也由大气和海洋中的过程引发。在以下论文(格雷维梅耶等,2000;阿斯特等,2008;凯达尔等,2008;席梅尔等,2011)中,研究了气候变化和海洋过程引起的微震场的变化。
为了使地震成为持续存在的微震振荡的来源,至少需要每天发生一次6级震级的地震,才能维持此类振荡的观测强度。根据古登堡–里希特定律估算的所有弱震的累积效应,其能量贡献比观测值小一到两个数量级。大气过程(气旋运动)及其产生的海洋波,以及这些波浪对陆架和海岸的冲击,对低频微震背景的能量贡献最大。关于主要周期为4分钟的低频地震嗡鸣的成因研究见于李和罗曼诺维奇(2004,2006)的研究。他们建立了这些振荡强度与海洋风暴波高之间的显著相关性,并指出嗡鸣强度与地球的地震活动无关:作者提供了一个地震平静的时间间隔(2000年1月31日–2月3日)的例子,尽管期间地震活动较弱,但在4分钟周期附近的微震背景却表现出异常高的振幅。作为此类振荡激发的一种可能机制,他们提出了由巨浪扰动引力场,从而在海底激发低频地震波。这些振荡的主要激发区域被认为是冬季的北太平洋和夏季的南大西洋。该频率范围的环境地震噪声(“地震嗡鸣”)已被研究(西田等人,2008年,2009年;福尾等人,2010年)。
尽管低频微震的主要能量来源是地壳外部的,而地壳仅作为传播介质,但地壳内部的条件会影响低频微震振动行为的统计特征和具体特征。因此,如果我们研究地震噪声特性的变化,这项研究有望提供有关地壳变化的重要信息,包括与地震过程及强震孕育相关的变化。
利用低频微震振荡监测岩石圈的这一基本而简单的想法,尽管如此,却无法简单实现。主要困难在于大量不相关的数据源具有强烈的干扰作用。这些数据源通常在地球表面呈弥散分布。因此,在这种情况下,无法通过控制输入作用与响应来研究岩石圈的传播特性。此外,在处理微震振荡时,传统数据分析方法中典型的“信号”与“噪声”的区分失去了意义。只有微震振幅中的潮汐变化,以及来自已知强地震的到时和尾波,才可被视为“信号”。这些信号长期以来一直在地球物理学中被传统使用。所有其他微震变化均属于“噪声”。
在本节中,克服非相关随机源影响的主要工具是利用在相邻的“短”时间段内计算的 (En;Δα; α∗)统计量。因此,地震噪声记录被转换为具有“大”采样时间步长的时间序列:例如1天。这些时间序列的相关性更高,更适合研究同步效应。
地震记录通过向位于http://www.iris.edu/forms/webrequest/的地震学联合研究机构(IRIS)数据库请求,从三个全球宽频带地震台站网络的229个地震台站获取:
- 全球地震台网:http://www.iris.edu/mda/_GSN;
- GEOSCOPE:http://www.iris.edu/mda/G;
- GEOFON: http://www.iris.edu/mda/GE。
垂直分量以1赫兹的采样率(LHZ记录)下载了从1997年1月1日到2016年12月31日的20年观测数据。初始的LHZ记录通过计算连续60秒时间段内的平均值,转换为1分钟的采样时间步长。进一步的分析基于对每日连续时间区间内1440个样本(时间步长为1分钟)的低频地震噪声波形(周期超过2分钟)的统计特性进行估计。
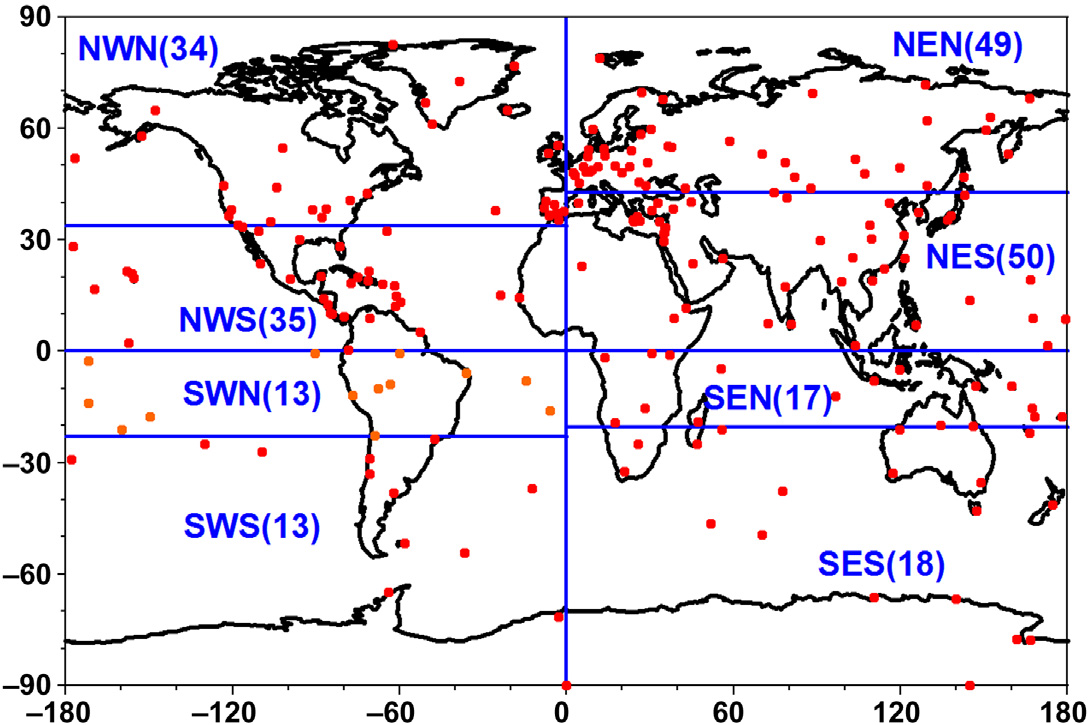 展示了全球229个宽带地震台站的位置,并将它们分为八个组。每个组都有一个三字母识别码,每组内的台站数量在括号中给出。这些组的名称具有以下缩写定义:第一个字母是“N”或“S”,表示北或南,分别用’E’或’W’表示东或西。因此,最初所有台站被划分为四个组,即东北、西北、东南和西南半球。最后,根据每个部分内的台站数量大致相等的原则,将这四个部分中的每一个再按南北两部分(第三个字母为’N’或’S’)进行划分。
展示了全球229个宽带地震台站的位置,并将它们分为八个组。每个组都有一个三字母识别码,每组内的台站数量在括号中给出。这些组的名称具有以下缩写定义:第一个字母是“N”或“S”,表示北或南,分别用’E’或’W’表示东或西。因此,最初所有台站被划分为四个组,即东北、西北、东南和西南半球。最后,根据每个部分内的台站数量大致相等的原则,将这四个部分中的每一个再按南北两部分(第三个字母为’N’或’S’)进行划分。
将每个台站的地震记录重采样至1分钟采样时间步长后,被划分为相邻的1天(1440个样本)时间段,并对每个时间段计算低频日地震噪声波形的三个参数。其中两个是多重分形参数:广义赫斯特指数α∗和奇异性谱支撑宽度 Δα。为了消除与尺度相关的趋势(主要由潮汐变化引起),在估计奇异性谱的方法中,公式(6.21)中使用了八阶局部多项式。另一个地震噪声参数是正交小波系数平方的最小归一化熵En。在每个每日时间窗口内计算熵En之前,从地震噪声波形中去除了八阶多项式趋势。因此,从
 所示的229个地震台站中的每一个都获得了采样时间步长为1天的α∗、Δα和En值的时间序列。
所示的229个地震台站中的每一个都获得了采样时间步长为1天的α∗、Δα和En值的时间序列。
 展示了数据变换操作的顺序。
展示了数据变换操作的顺序。
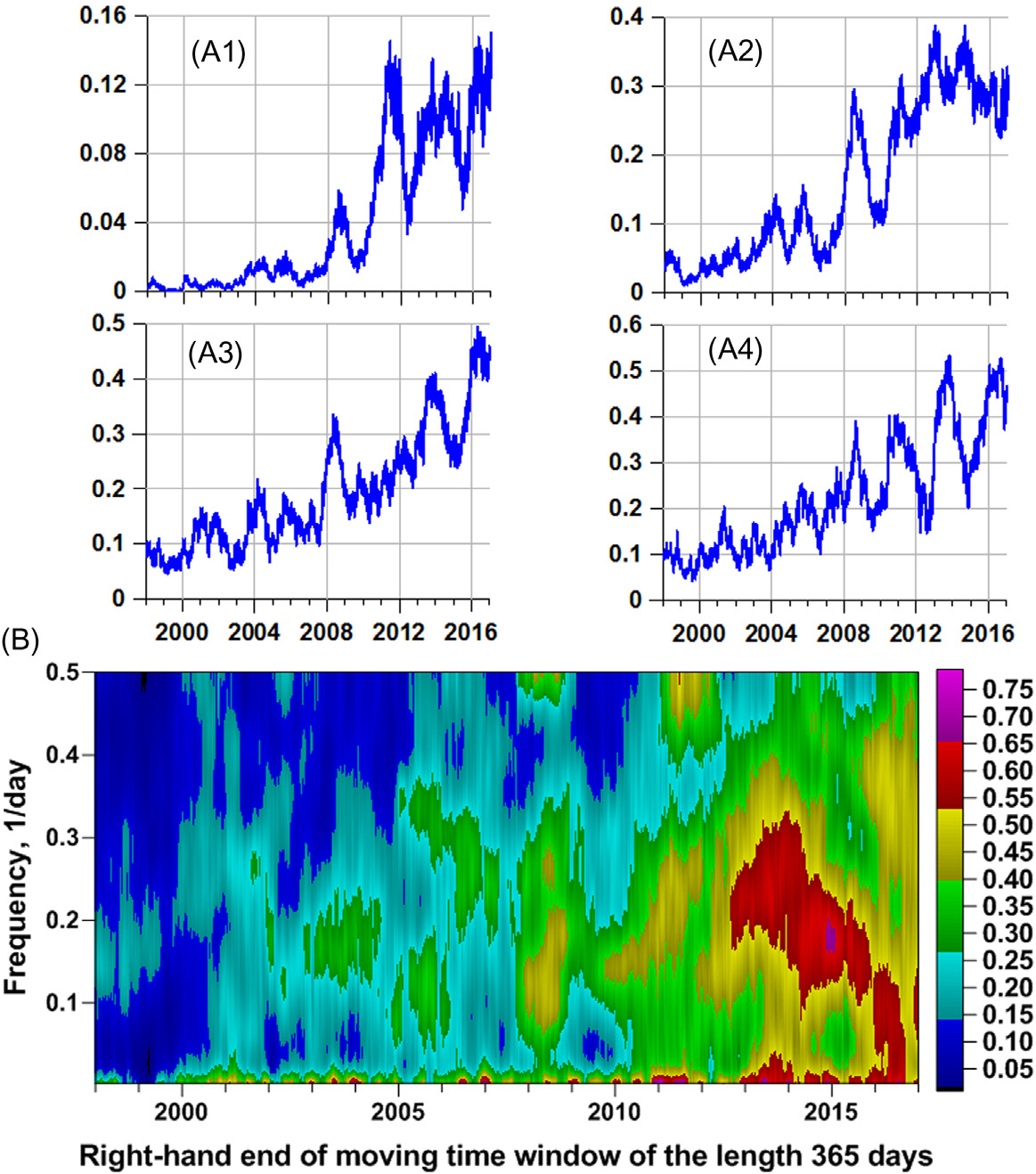 展示了北半球四个区域NWN(西北北)、NEN(东北北)、NWS(西北南)和NES(东南北)的多重分形奇异性谱支撑宽度的日中位数值 Δα、广义赫斯特指数α∗以及正交小波系数平方的最小归一化熵En,以及利用公式(6.28)基于365天长度的适应期,从北半球和南半球全部八个区域的日时间序列(En;Δα;α∗)计算得到的第一主成分。从57天窗口内的移动平均图可以看出,所有区域均表现出强烈的年周期性。特别是对于西北北和东北北方向。我们相信这种周期性是由强海洋风暴的季节性周期影响所致,众所周知,强海洋风暴是永久性地震噪声的重要能量来源(瑞和罗曼诺维奇,2004年,2006年;西田等人,2008年,2009年;福尾等人,2010年)。
展示了北半球四个区域NWN(西北北)、NEN(东北北)、NWS(西北南)和NES(东南北)的多重分形奇异性谱支撑宽度的日中位数值 Δα、广义赫斯特指数α∗以及正交小波系数平方的最小归一化熵En,以及利用公式(6.28)基于365天长度的适应期,从北半球和南半球全部八个区域的日时间序列(En;Δα;α∗)计算得到的第一主成分。从57天窗口内的移动平均图可以看出,所有区域均表现出强烈的年周期性。特别是对于西北北和东北北方向。我们相信这种周期性是由强海洋风暴的季节性周期影响所致,众所周知,强海洋风暴是永久性地震噪声的重要能量来源(瑞和罗曼诺维奇,2004年,2006年;西田等人,2008年,2009年;福尾等人,2010年)。
来自全球八个部分的第一主成分时间序列构成多变量时间序列,这是应用基于小波和谱相干性度量的对象,旨在检测全球地震噪声特性中的相干性效应。365天移动时间窗口的长度在该应用中非常自然。
 展示了相干性度量估计的结果。
展示了相干性度量估计的结果。
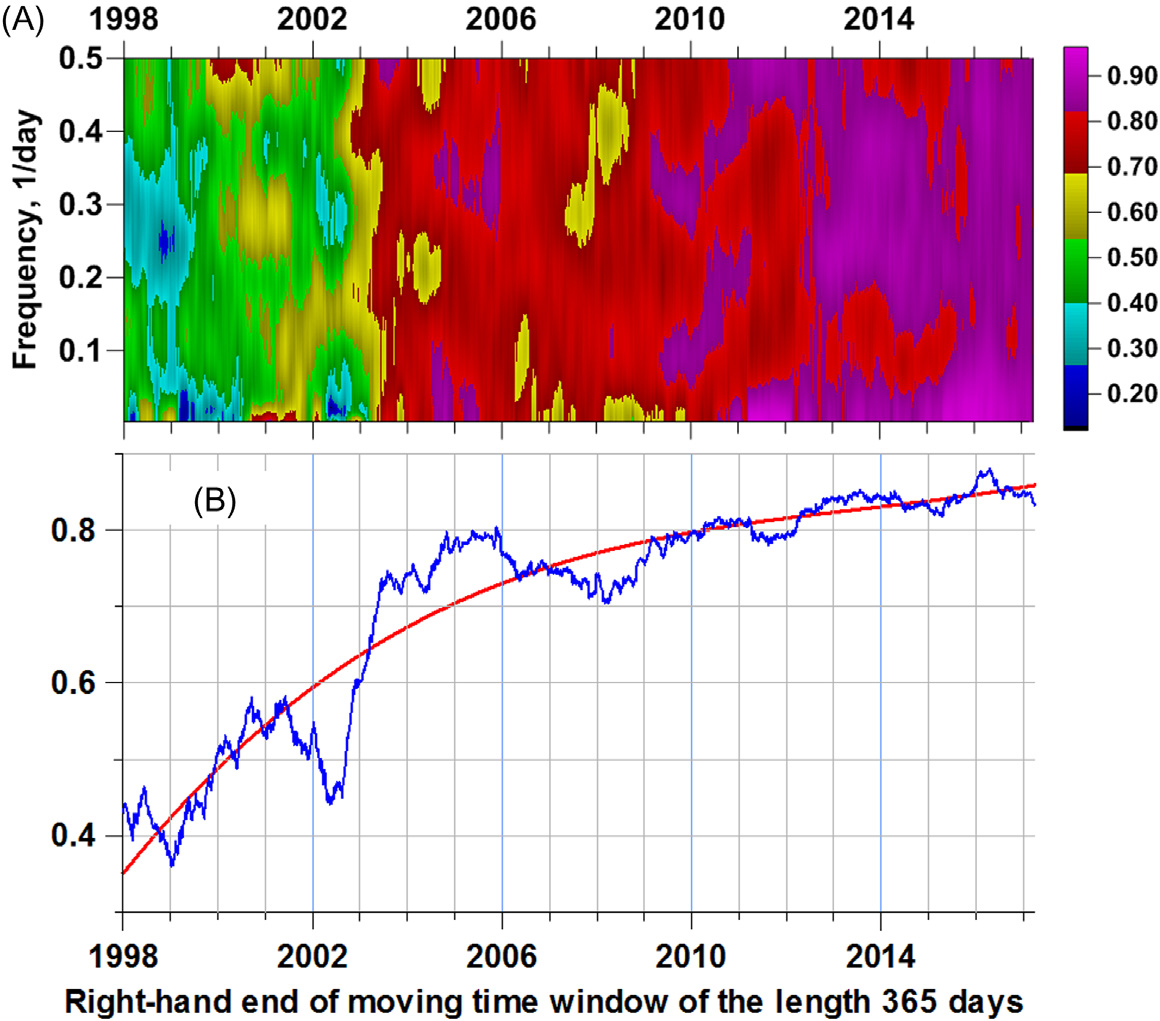
 展示了使用哈尔小波对四个细节层次(尺度范围分别为 2–4, 4–8, 8–16和 16–32天)的基于小波的度量 ρ(τ; β)[(公式(6.7))的演化情况。小波分解前四个细节层次的出现是由于时间窗口的365个样本长度以及显著性阈值Lmin= 16的结果。
展示了使用哈尔小波对四个细节层次(尺度范围分别为 2–4, 4–8, 8–16和 16–32天)的基于小波的度量 ρ(τ; β)[(公式(6.7))的演化情况。小波分解前四个细节层次的出现是由于时间窗口的365个样本长度以及显著性阈值Lmin= 16的结果。
 中的图是相对于移动时间窗口右端的时间绘制的。这些图的主要特征是相干性的增加,从移动时间窗口位置 2007–08开始可以观察到这一现象。这种增加不是渐进的,在总体上升趋势背景下,具有约 2–3年的较强波动。
中的图是相对于移动时间窗口右端的时间绘制的。这些图的主要特征是相干性的增加,从移动时间窗口位置 2007–08开始可以观察到这一现象。这种增加不是渐进的,在总体上升趋势背景下,具有约 2–3年的较强波动。
时间–频率图中的相干谱测度 λ(τ; ω) [式(6.15)]在
 中证实了这一结论。
中证实了这一结论。
 是通过在长度为365个样本的移动时间窗口内,使用五阶向量自回归模型[式(6.12)]对 λ(τ; ω)进行估计得到的。因此,无论是使用小波(紧支基函数)还是傅里叶谱方法独立地分析来自全球各地台站的地震噪声特性变化,均提取到了相同的相干性增强效应。
是通过在长度为365个样本的移动时间窗口内,使用五阶向量自回归模型[式(6.12)]对 λ(τ; ω)进行估计得到的。因此,无论是使用小波(紧支基函数)还是傅里叶谱方法独立地分析来自全球各地台站的地震噪声特性变化,均提取到了相同的相干性增强效应。
 提供了20世纪初以来发生的20次最强地震的相关信息。根据表 6–1,中自20世纪初以来发生的20次最强地震的信息,自2001年中期以来已发生了七次事件,其中四次发生在2007年9月之后。结果表明,全球地震噪声特性的相干性增强与最强地震发生频率的显著上升相吻合,这一现象自2004年12月26日苏门答腊特大地震以来尤为明显,特别是自2007年起。考虑到我们研究的周期范围从2分钟到500分钟,这种相干性增强不可能是这些最强地震余震的直接结果。我们的假设是,在为大地震准备的区域,地球’地壳小块体的缓慢运动出现了同步(柳布申,2009,2010b,2011a,b,2012,2013a,b)并且我们看到,这种同步现象是一个自2000年代初开始的全球性现象(柳布申,2014a,2015)。观测到的地震噪声同步增强可能是未来不久将发生的最强地震的前兆。
提供了20世纪初以来发生的20次最强地震的相关信息。根据表 6–1,中自20世纪初以来发生的20次最强地震的信息,自2001年中期以来已发生了七次事件,其中四次发生在2007年9月之后。结果表明,全球地震噪声特性的相干性增强与最强地震发生频率的显著上升相吻合,这一现象自2004年12月26日苏门答腊特大地震以来尤为明显,特别是自2007年起。考虑到我们研究的周期范围从2分钟到500分钟,这种相干性增强不可能是这些最强地震余震的直接结果。我们的假设是,在为大地震准备的区域,地球’地壳小块体的缓慢运动出现了同步(柳布申,2009,2010b,2011a,b,2012,2013a,b)并且我们看到,这种同步现象是一个自2000年代初开始的全球性现象(柳布申,2014a,2015)。观测到的地震噪声同步增强可能是未来不久将发生的最强地震的前兆。
6.7 日本岛屿的低频地震噪声
本节主要关注对日本岛屿地震噪声数据的处理。这一特点源于以下事实:在仪器地震学最近的一个时期内,2011年3月11日在日本发生了一次震级为9.1的特大地震,而日本是一个地球物理观测网络极为密集的区域,其观测数据可通过互联网公开获取。这种结合为检验不同假设提供了独特的机会,即地震灾难准备过程如何影响活动区域内地震噪声的统计特性。
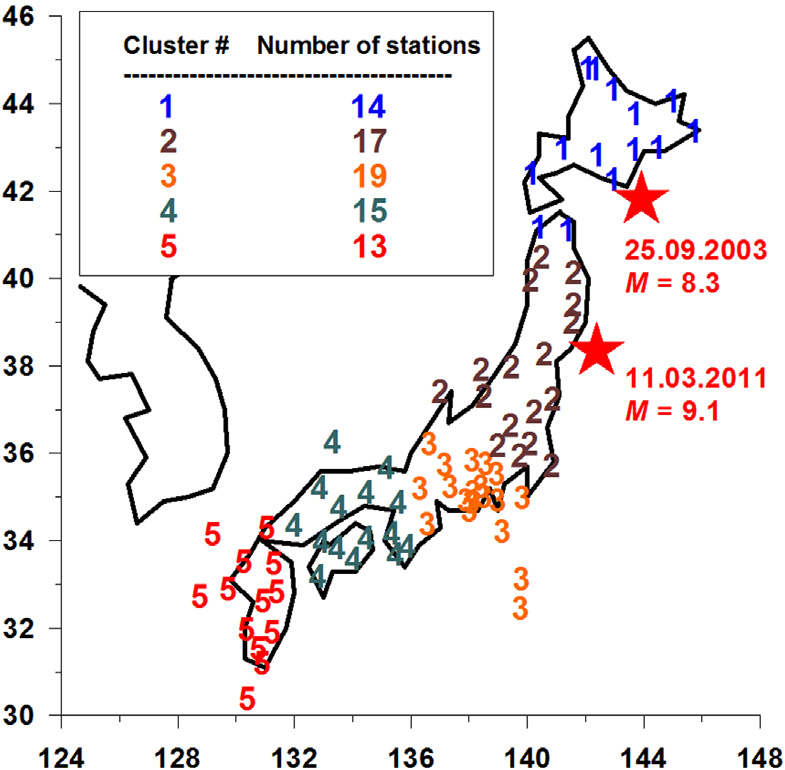
本分析所用的垂直宽带地震振荡分量(LHZ记录)采样时间步长为1秒,数据来自日本宽带地震网络F-net台站,从1997年初开始至2017年8月31日,从以下互联网地址下载 http://www.fnet.bosai.go.jp。F-net地震台站的完整列表共包括84个位置。我们选取了位于 30°北以北的台站,从而排除了位于偏远小岛上的六个孤立台站的数据。用于分析的78个台站的位置如
 所示,并标出了观测期间发生的两次最强地震的震中:2003年9月25日北海道附近发生的8.3级地震,以及2011年3月11日发生的东日本大地震(震级9.1)。这78个台站被划分为五个群集,在
所示,并标出了观测期间发生的两次最强地震的震中:2003年9月25日北海道附近发生的8.3级地震,以及2011年3月11日发生的东日本大地震(震级9.1)。这78个台站被划分为五个群集,在
 中用不同颜色的数字表示各个群集。
中用不同颜色的数字表示各个群集。
F网地震数据经过转换,通过计算相邻的60秒时间窗口内的平均值,得到1分钟采样时间步长的数据,并进一步分析在具有1分钟采样时间步长的1440个样本的相邻时间窗口内,即1天的时间窗口内,计算 (En;Δα; α∗)的值(见
 )。
)。
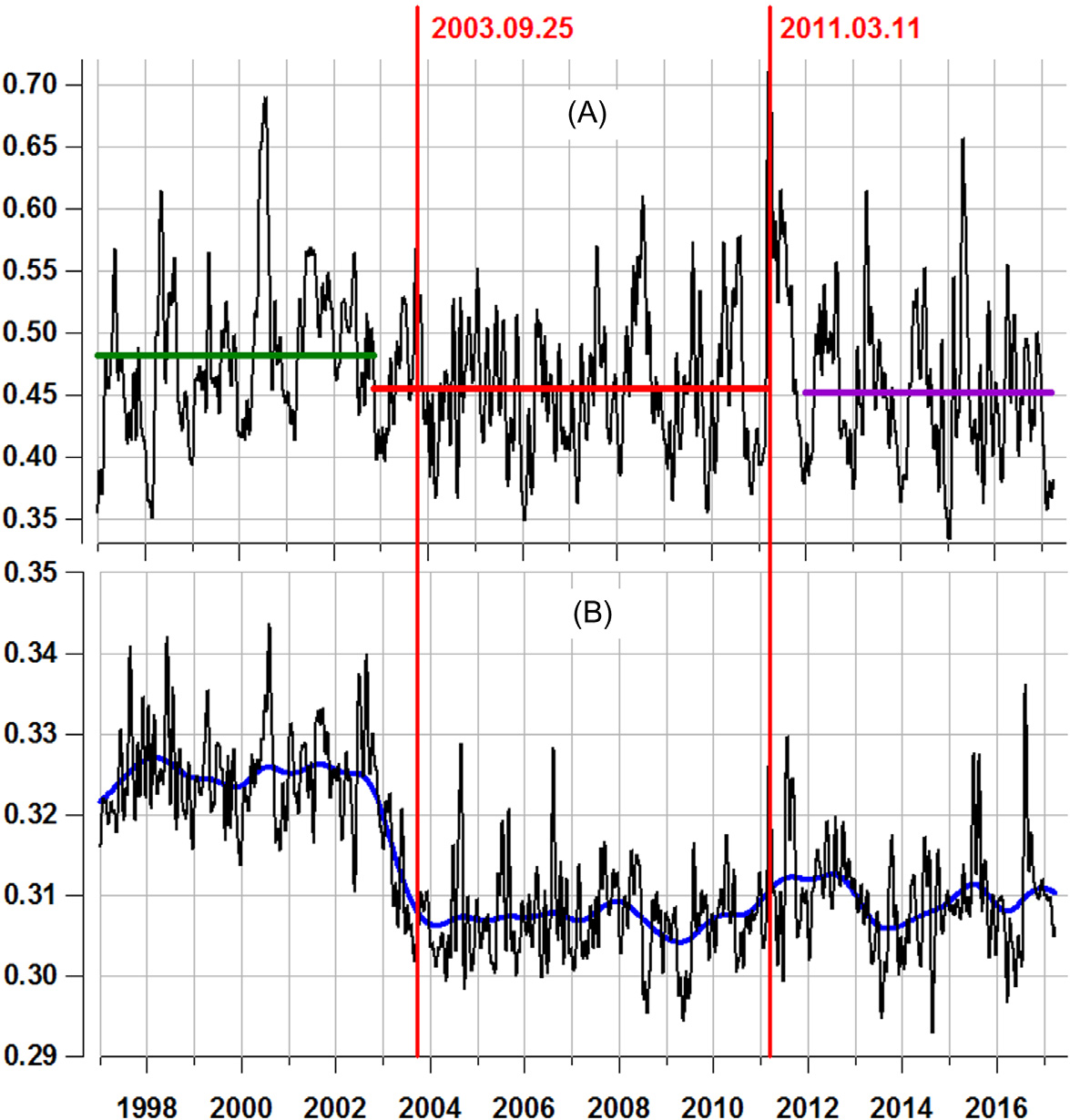
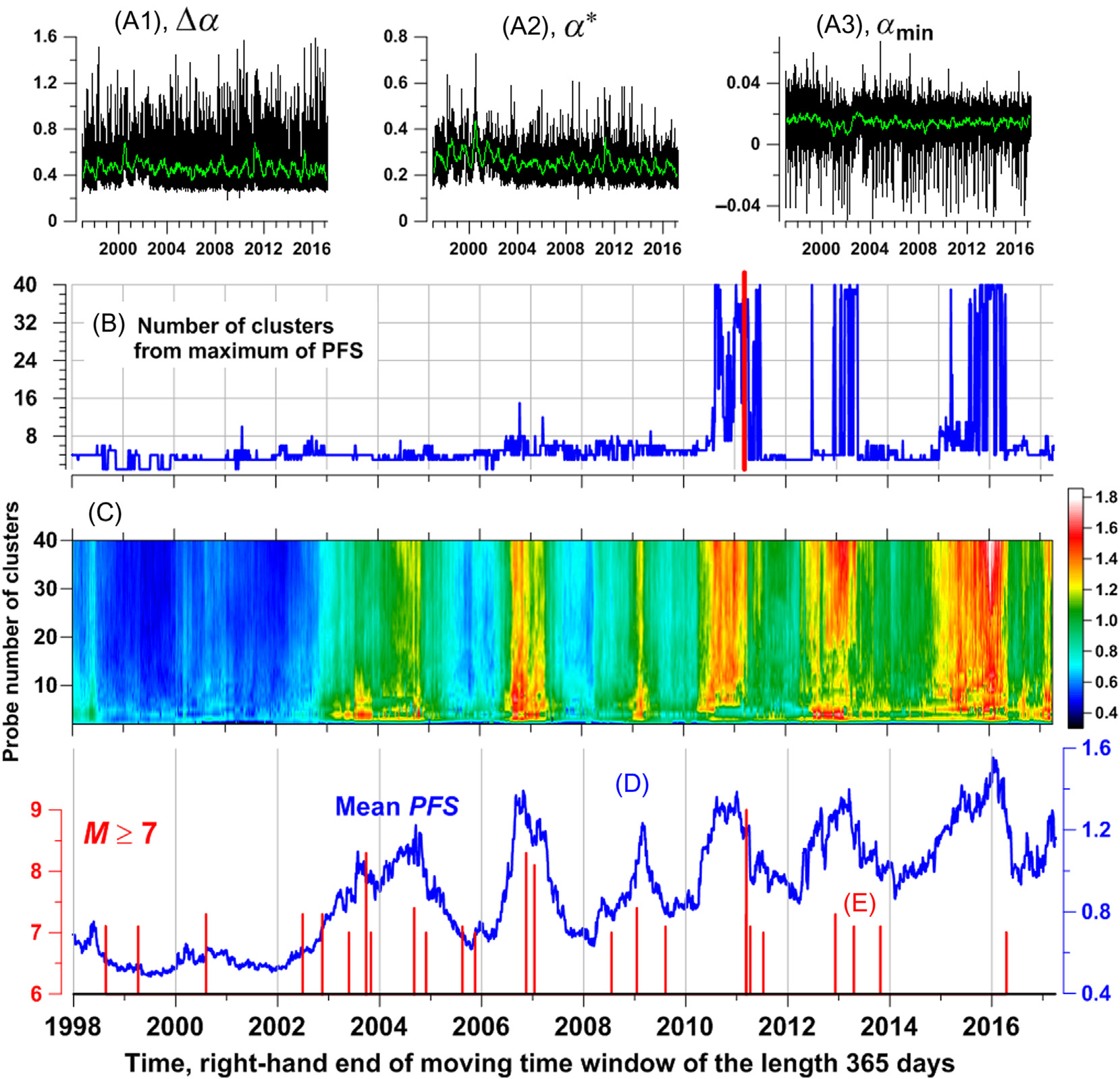
让我们详细分析Δα的时间序列。对每个时间窗口,我们计算所有可运行台站的 Δα估计值的中位数值,从而得到Δα(m)中位数值的标量时间序列,作为整个网络地震噪声的积分特征。我们特别关注Δα(m),因为已知奇异性谱支撑宽度的减小是复杂系统向临界状态转变的一个指标,此时环境噪声的结构变得更简单(多分形性减弱),并可能预示着某些灾难性变化的发生。
需要注意的是,利用多重分形奇异性谱支撑宽度研究非线性系统行为已有较长的历史。特别是“多分形性丧失”,即奇异性谱支撑宽度减小,是系统特性发生突变前的一个众所周知的现象。这一现象主要在生物和医学系统中进行了研究(伊万诺夫等,1999;胡莫瓦等,2008;杜塔等,2013),但在帕夫洛夫和阿尼先科(2007)的研究中表明,该现象具有相当普遍的性质,在物理系统中也同样存在。地震噪声波形奇异性谱支撑宽度变窄与其他非线性系统中多分形性丧失之间的类比,促使作者提出了将日本列岛用于地震灾害研究的假设(柳布申,2008a)。
在分析Δα(m)的特性之前,让我们通过公式(6.29)对信号 Δα(m)(t) 使用高斯核平滑
$$
ξ(t|h) = \int Δα(m)(t + h s) \cdot ψ(s) ds; \quad ψ(s) = \frac{\exp(-s^2/2)}{\sqrt{2π}}
\quad (6.29)
$$
其中 h > 0 是一个平滑参数,可称为高斯平滑的平均半径。以 13天 的平均半径对 Δα(m) 进行平滑后的值在 中用黑线表示。
两条红色垂直线表示最强地震发生的时间点,它们将 ξ(t|h) 的历史分割为三个片段的序列。第一个时间段属于2003年9月25日北海道地震之前的时间间隔。可以看出,该片段中 ξ(t)的平均值大于2011年3月11日东北地震之前其他时间间隔的平均值。让我们找出时间点 tC 使用方差分析(ANOVA)中的费舍尔准则(拉奥,1965)对北海道地震发生时刻附近 ξ(t) 的平均值的最大变化进行分析。计算在所有分析的时间区间内 ξ(t) 的总体平均值 ξ₀ = (1/N)∑ {t=1}^N ξ(t),其中 N 为样本和左右两侧探查时刻 tC 的平均值的总数: ξ₁ = (1/tC)∑ {t=1}^{tC} ξ(t) 和 ξ₂ = (1/(N−tC))∑_{t=tC+1}^N ξ(t)。变点 tC 由以下条件确定
$$
F(t_C) = \frac{S_1^2(t_C)}{S_2^2(t_C)} \to \max
\quad (6.30)
$$
其中
$$
S_1^2(t_C) = t_C (ξ_1 - ξ_0)^2 + (N - t_C) (ξ_2 - ξ_0)^2;
$$
$$
S_2^2(t_C) = \frac{1}{N-2} \left( \sum_{t=1}^{t_C} (ξ(t) - ξ_1)^2 + \sum_{t=t_C+1}^N (ξ(t) - ξ_2)^2 \right)
\quad (6.31)
$$
使用判据(6.30)检测到2002年11月8日为变化点tC ,其对应的平均值分别为0.482和0.454,对应于ξ₁和 ξ₂。这些平均值在中用粗的绿色和红色平行线表示。该Δα(m)的下降表明某种瞬态地球动力学过程开始向不稳定状态转变,这一过程始于2003年9月25日北海道地震的前兆阶段。在东日本大地震之后,Δα(m)的平滑值迅速上升,这是大地震后地壳内部应力松弛过程的响应。然而,从2012年初开始,Δα(m)的平均平滑值恢复至此前约 0.452的水平。这意味着2011年3月11日的东日本大地震并未使该区域恢复到北海道地震前的 “正常”状态,目前仍处于高地震危险状态。
在2003年9月25日北海道地震前后,若对相邻的30分钟(1800个样本)时间窗口内采样时间步长为1秒的初始垂直地震记录的平均值进行估计,则其平均值之间的差异变得更加明显。在这种情况下,通过去除四阶多项式局部趋势,使用去趋势波动分析(DFA)计算了多重分形奇异性谱。在中,黑线表示这些 Δα值经高斯平滑处理后的结果,平均半径为13天,而粗蓝线的平均半径为0.5年。显示了在2003年9月25日地震前Δα出现与相同的下降现象。
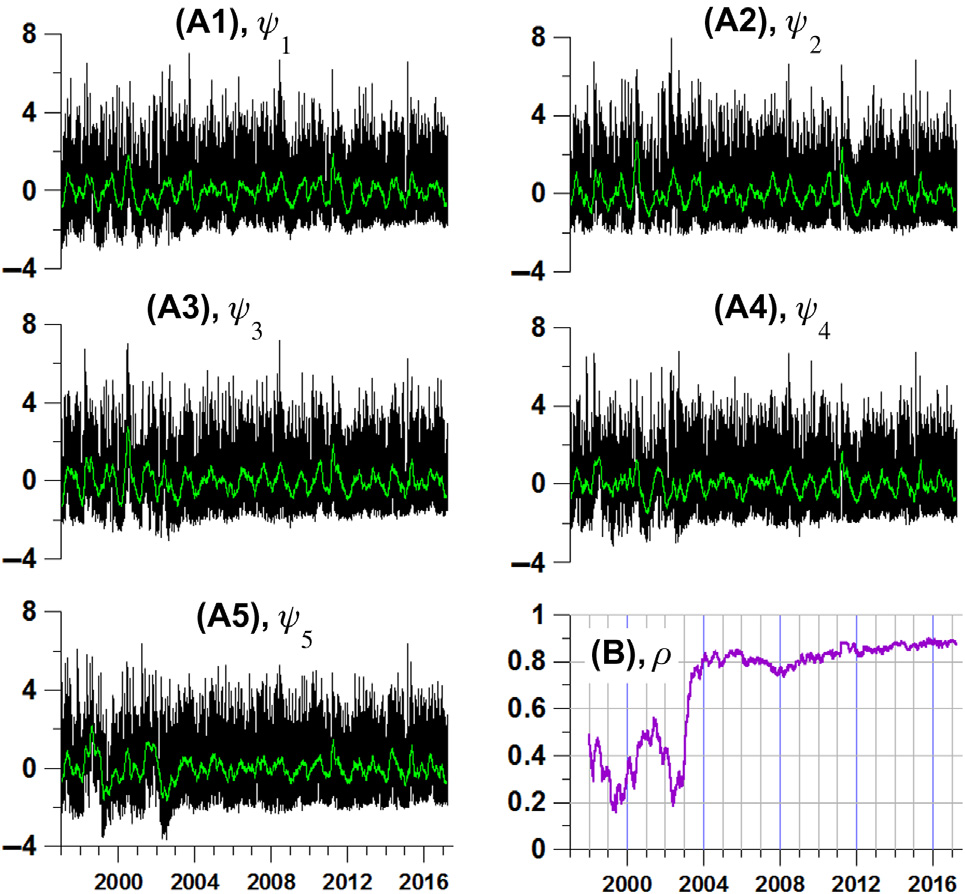
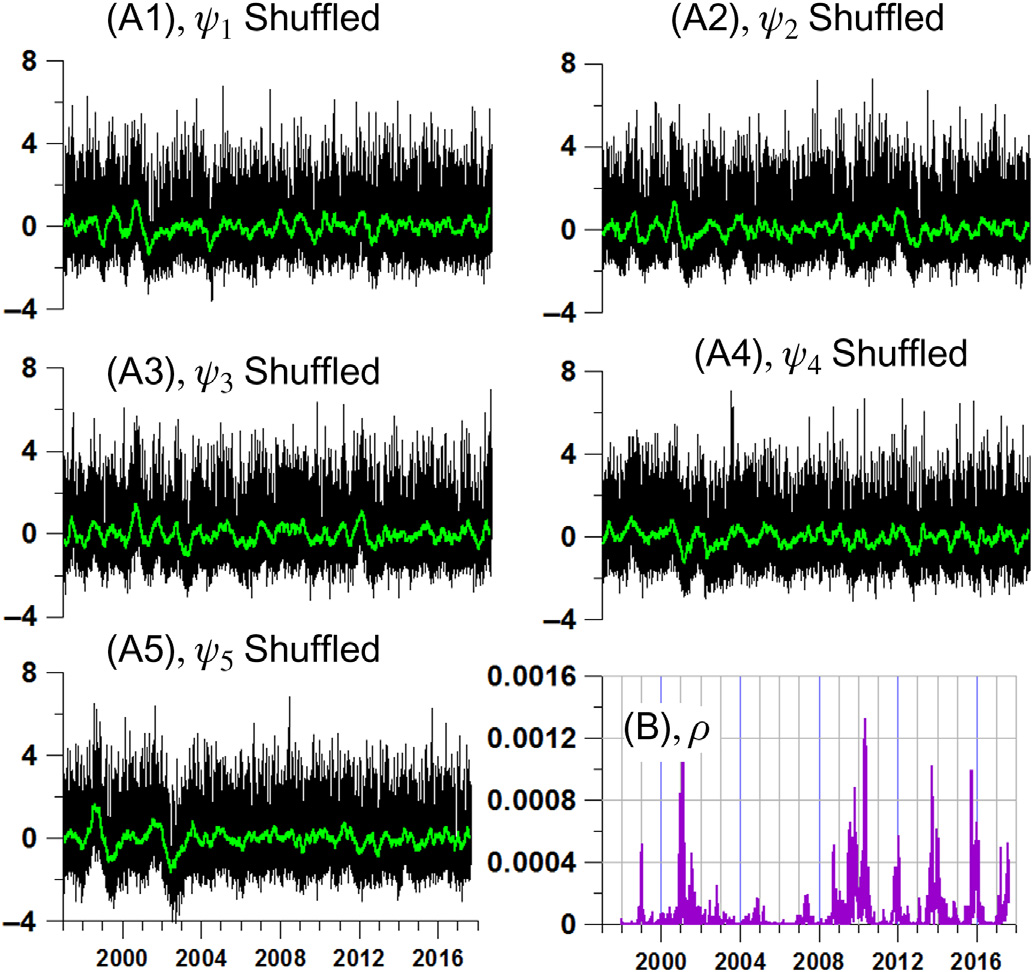
让我们考虑中所示的五个台站群。我们关注的是从该网络这五个部分计算出的每日地震噪声属性中位数值之间相干性效应的时间依赖性演化。为此,让我们计算第一主成分ψk(t); k= 1;…;5,这些第一主成分基于每个台站群内所有运行台站每日估计的参数(En;Δα; α∗) 的中位数值计算得到,如所示。这些第一主成分是在365天的自适应滑动窗口内使用公式(6.28)计算得出的。 中展示了这些第一主成分。相干性的最简单度量是平方稳健多重相关系数 ρ[式(6.8)],,如 所示,该值在长度为365天的移动时间窗口中进行估计。我们可以看到, ρ在位于区间 2002–04, 的时间窗口内表现出快速增加,即在2003年9月25日北海道地震发生前后。地震噪声相关性的这一特性独立地证实了从分析中得出的结论:2002年是日本岛屿地震噪声结构发生快速变化的一年,这是2011年3月11日未来地震灾难孕育的征兆。从这个意义上讲,尽管震级不大,2003年9月25日的北海道地震可被解释为2011年3月11日东北地震的前震。如果继续比较和 ,我们还可以注意到另一个共同点:东日本大地震在Δα的中位数值以及多重相关性ρ的值上均表现出短期响应。这意味着东日本大地震并未改变地震噪声的相关性结构,而且这种相关性反而增强,因为 ρ在2012年之后呈现出轻微的正趋势。
有趣的是,通过另一种方法——相干性估计——来获得关于地震噪声相关性增长这一结论的独立验证借助多重谱测度[公式(6.10)]。为此,我们考虑一个五维的第一主成分时间序列ψk(t);k= 1;⋯;5,并利用五阶向量自回归模型[公式(6.12)] ,在365天移动时间窗口内计算多重谱相干测度[公式(6.10)]。中的时频二维图展示了该估计结果,而显示了使用每个时间窗口内的所有频率值对相干性度量[公式(6.10)]进行时间依赖性平均λmean(τ)的结果[公式(6.16)]。
相干估计的结果如所示,证实了从中多重相关性 ρ行为分析得出的结论:尽管2011年3月11日发生了东日本大地震,地震噪声相干效应在 2002–04的瞬态过程之后变得更强,并呈现出略微的正趋势,且该趋势至今仍在持续。利用中的时频图可以直观地展示相干性增长的频率分解情况,我们可以看到这种增长实际上与频带无关。
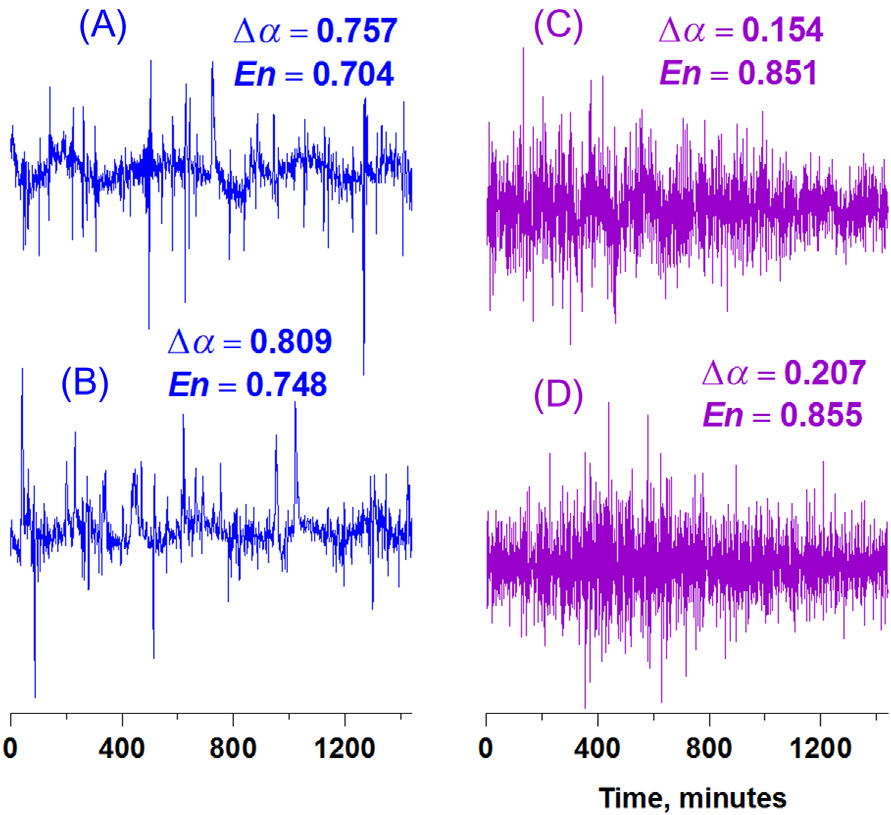
所使用的地震噪声参数之一是小波系数平方的归一化熵En。该量是Δα的一种对立参数。展示了四个示例不同 Δα和En值的每日噪声波形: 和 B左侧图显示了具有高 Δα值和低En值的噪声波形,而右侧图( 和 D)对应两个具有低 Δα值和高En值的噪声波形。、B 与 C、D 之间波形特征的差异明显:高Δα值和低En值的出现是由于存在不规则的高幅值尖峰,这些尖峰以平稳行为的间隔呈间歇性分布。这是一种典型的多重分形:可观察到不同类型的随机行为。低 Δα值则对应更为平稳的行为:噪声结构更简单且多分形性减弱。
我们的假设是,Δα的低值与地震危险性的增长之间存在相关性。因此,熵En的增加也可能与地震危险性的增加有关。关于 Δα的低值和En的高值能够识别地震危险区域的能力,Lyubushin(2012, 2013a,b)给出了可能的物理解释。这是强震前地壳小块体合并为大块体的结果。这种合并意味着地震噪声中不再包含与小块体相互运动相关的尖峰。噪声中不规则尖峰的消失导致了Δα的降低和熵En的升高。
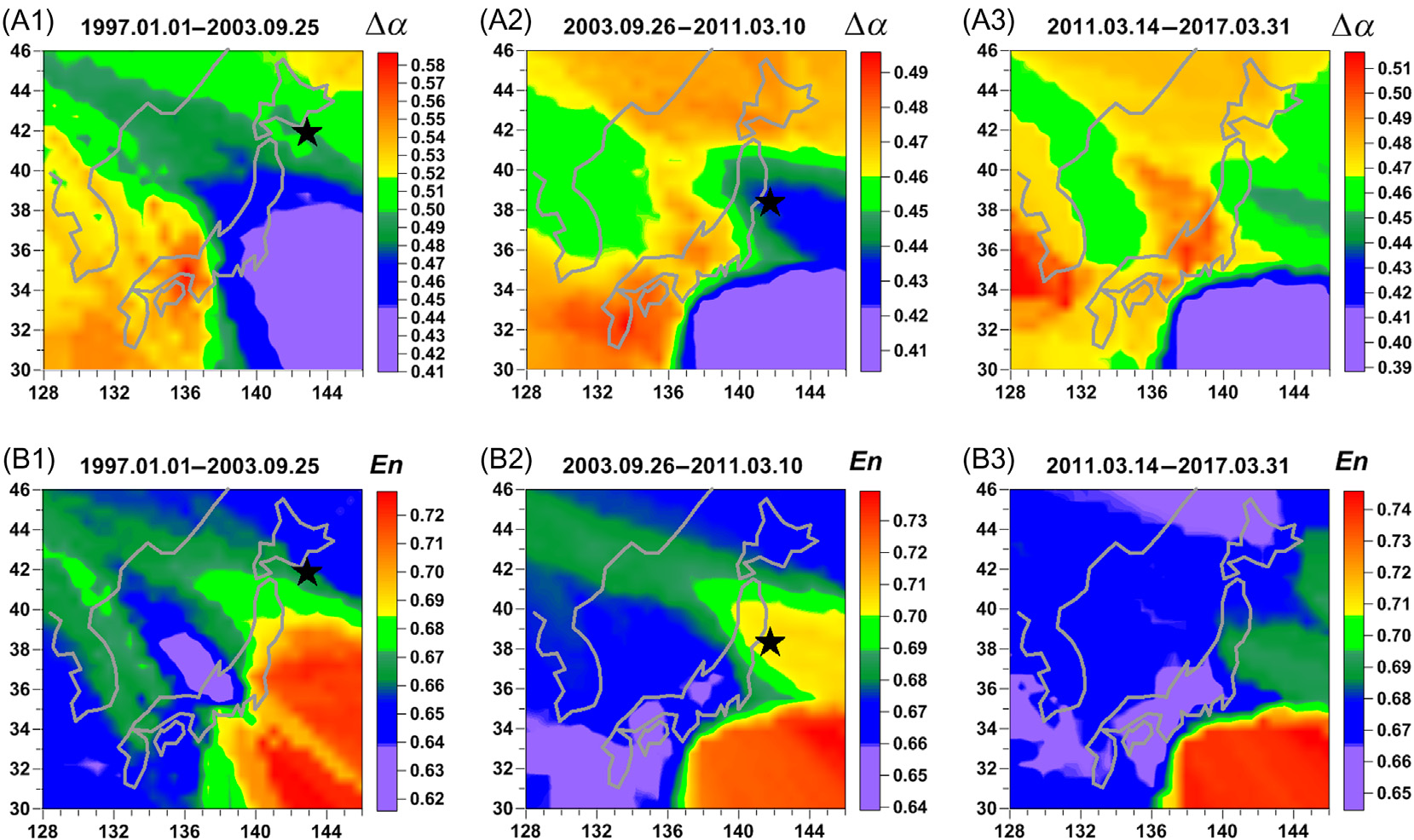
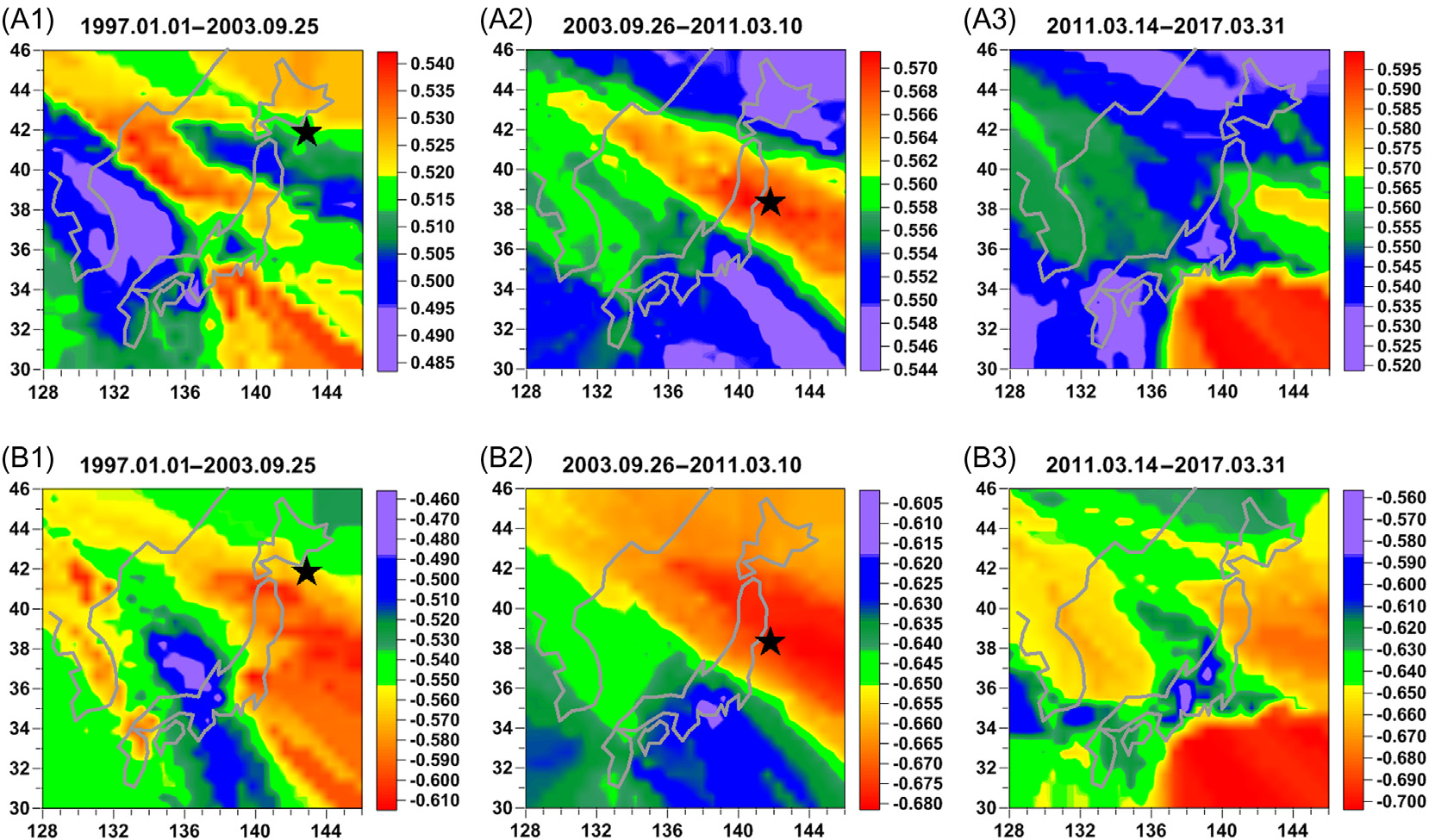
获取所有Δα和En地震台站的值后,可以绘制这些地震噪声统计量的空间分布地图。为此,我们考虑一个覆盖纬度30至46°N、经度128至148°E矩形区域的30×30个节点的规则网格(见)。对于该网格中的每个节点,相应的Δα和En日值通过该节点对应的最近的五个可操作地震台站的值的中位数计算得到。
展示了三个相邻时间段的平均地图 Δα和 En:从1997年初至2003年9月25 日,即北海道附近发生8.3级地震的当天;从2003年9月26日至2011年3月10日,即2011年3月11日9.1级东日本大地震的前一天;以及从2011年3月14日至2017年8月31日。由于2011年3月11日地震冲击后F网的许多地震台站在这三天(2011年3月11日、12日和13日)无法正常工作,因此这三天被排除在分析之外。
显示,绘制奇异性谱支撑宽度空间分布的平均地图Δα可以提取未来灾难发生的位置,即值相对较低的区域Δα。展示了一幅地图,其中存在一个相对较低的Δα区域,可以看出,该区域包括未来大地震发生的位置,并且尚未分裂为南北两部分。在中可以看到,2003年9月25日事件之后,该区域分裂为南北两部分,其中北部成为2011年3月11日日本大地震余震发生的区域,而南部则在2011年3月11日前后始终保持较低的奇异性谱支撑宽度 Δα值()。根据对低 Δα值区域具有地震危险性的解释,我们可以提出一个假设:在东北地震期间,仅释放了部分积累的地震能量,上述南部区域(菲律宾海板块的北部,南海海槽)可能成为未来大地震的发生区域。这一假设解释了为何在2011年3月11日之后地震噪声的相干性仍然保持较高水平(和 6–8)。
证实了这一结论,该结论是通过分析,中的图表得出的:最小归一化熵 En是参数 Δα的对立参数,且上述关于 Δα性质的几乎所有内容,在将“最小” 替换为“最大”后,都可适用于En:相对较高的归一化熵值出现在地震前的地震危险区域。我们将用Δα低值和En高值识别出的区域称为“地震危险点”(SSD)。Δα和En的平均值呈强负相关 ,因此Δα和En的统计结果获得的SSD大致相同。尽管如此,综合考虑这两个参数仍是必要的,因为它们基于不同的方法。Δα和En的地图可以在移动时间窗口 –中依次绘制,此类估计提供了可视化SSD起源与演化的可能性。
预测日本南海海槽地区的最强地震问题一直是日本地震学家的一个重大传统课题(理学 家力武,1999年;茂木,2004年)。在Rikitake(1999)中,对菲律宾海板块接近日本中部的东海–南海地区发生震级大于8.5地震的概率进行了估计,结果为0.35–0.45“在2000年之后的10年期间”。在Simons 等人(2011)中,基于GPS数据的分析,在东北地震发生后立即评估了日本的地震危险,并得出结论:“估计…表明有必要考虑此次事件以南发生未来大地震的可能性。”在Kagan 和 Jackson(2013)的论文中,讨论了为何东北地震令科学界感到意外的问题。其中一个结论是‘东北外海发生震级9的地震本不应令人意外’。该结论是通过对地震目录的回溯分析得出的。然而,东北地震事件对于所有传统的地震预测方法而言仍是一个巨大的意外。另一个结论来自Zoller 等人(2014),即即使在日本海沟发生震级 10地震也是完全可能的。
参数对之间相关性的地图(α∗;Δα)和(α∗;En)具有有趣的预测特性。类似于中所示的地图,我们可以绘制(α∗;Δα)增量之间相关性的平均地图。为此,让我们在365天移动时间窗口内估计每个台站a的(α∗;Δα)之间相关系数的演化。对于1年移动时间窗口的每个位置,我们可以通过计算五个可运行的地震台站的相关系数中位数来绘制一幅地图这些点最接近规则网格的每个节点。平均地图是通过对所有完全位于两个给定日期之间(包括这两个日期)的1年时间段对应的地图进行平均而创建的。类似地,可以绘制出对(α∗;En)的相关系数地图;此类地图如所示。值得注意的是,在和B2中,未来东北地震区域表现出相对较高的相关性绝对值。注意,中的相关性为负值。对于东北地震之后的时期,根据和B3,SSD区域与相关性绝对值最大值区域一致 ,见和B3。
让我们增加一个独立的多重分形参数,并考虑以下三个中位数值 (Δα;α∗; α_min)其中 α_min是最小Hölder–Lipschitz指数。展示了这些值的图像。在移动时间窗口内,考虑这些每日序列三维向量的点云聚类特性,可以估计地震危险中的自然波动,甚至发现其周期性结构。
考虑一个长度为 L = 365天 的移动时间窗口,令 ~ξ(t)=(Δα; α∗; α_min)(t) 表示当前时间窗口内的三维向量,t = 1, …, L,其中 t 为时间索引,用于对向量进行编号。我们的目的是研究每个一年时间窗口内三维向量点云~ξ(t)的聚类特性。特别是,我们关注最佳的聚类数量是多少。
在执行聚类过程之前,对每个时间窗口内的每个向量的标量分量k 进行了归一化和迭代剔除离群值(Huber 和 Ronchetti,2009)的预处理操作。其中k = 1, 2, 3为向量~ξ(t)的标量分量的索引。设 ξ_k = (1/L)∑ {t=1}^L ξ(t)_k、 σ²_k = (1/(L−1))∑ {t=1}^L(ξ(t)_k − ξ_k)²分别为三维向量 ~ξ(t)的标量分量的平均值和方差的样本估计。我们进行若干次迭代,将数值 ζ(t)_k=(ξ(t)_k − ξ_k)/σ_k调整,并剔除超过阈值 ±3σ_k的 ζ(t)_k值。当 ξ_k和 σ_k的值变得稳定并等于以下数值 ξ_k= 0, σ_k= 1时,停止迭代。完成此预处理操作后,在每个当前时间窗口内得到由L个三维向量组成的点云~ζ(t)。
让我们使用标准的 k‐means 聚类过程(Duda 等,2000)将某个点云划分为给定数量 q 的簇。设 Γ_r;r = 1;…;q 为簇,z_r = (∑ {~ζ ∈ Γ_r} ~ζ)/n_r 为簇中心的向量,n_r 为簇 Γ_r 内向量 ~ζ(t) 的数量,∑ {r=1}^q n_r = L。若向量 ~ζ(t) ∈ Γ_r 到所有簇中心位置的距离 ||~ζ(t)−z_r|| 中为最小值,则其属于该簇。k‐means 过程最小化总和
$$
S(\mathbf{z}
1, …, \mathbf{z}_q) = \sum
{r=1}^q \sum_{\tilde{\zeta} \in \Gamma_r} ||\tilde{\zeta} - \mathbf{z}
r||^2 \to \min
{\mathbf{z}_1, …, \mathbf{z}_q}
\quad (6.32)
$$
关于聚类中心 z_r 的位置。令 J(q) = min_{z_1,…,z_q} S(z_1; …; z_q)。我们在范围 2 ≤ q ≤ 40 内尝试不同的试探性聚类数量。最佳聚类数量 q* 的选择问题通过伪F统计量的最大值 (Vogel, Wong, 1979)来解决,该方法类似于方差分析中的 F准则 [式(6.30)]:
$$
PFS(q) = \frac{\sigma_1^2(q)}{\sigma_0^2(q)} \to \max_{2 ≤ q ≤ 40}
\quad (6.33)
$$
其中
$$
\sigma_0^2(q) = \frac{J(q)}{L - q}; \quad \sigma_1^2(q) = \sum_{r=1}^q \nu_r ||\mathbf{z}_r - \mathbf{z}_0||^2
$$
$$
\nu_r = \frac{n_r}{L}; \quad \mathbf{z}
0 = \frac{1}{L} \sum
{t=1}^L \tilde{\zeta}(t)
\quad (6.34)
$$
PFS 最大化规则在我们尝试区分 q = 1和 q = 2的情况时不起作用,因为当 q = 1 时,σ²₁(q) 的值未定义。这些情况可以通过单调函数 J(q) 在参数 q = 2 处存在的拐点来区分(Lyubushin, 2011a)。 σ²₀(q) 的值随着 q 减小而单调增加,通常 log(σ²₀(q)) 对 log(q) 的依赖关系接近线性,即按 q⁻μ 进行尺度变换。众所周知,最优聚类数量也可以通过单调依赖关系 σ²₀(q) 在 q = q 范围内的拐点来确定:当 q 减小时,函数 σ²₀(q) 在 q < q 时的增长速度比在 q > q 时更快。这种确定聚类数量的规则被称为“肘部方法”(Ketchen, Jr and Shook, 1996)。该识别 q = q 的准则对噪声更敏感,性能也比技术 q = argmax PFS(q) 更差,但这是唯一能够区分 q = 1与 q* = 2 的方法。令 δ(q) 表示 log(σ²₀(q)) 相对于最佳拟合直线逼近 log(q) 依赖关系的偏差,即由公式 δ(q) = log(σ²₀(q)) − (a log(q) + b) 定义,其中系数 (a; b) 通过最小二乘法求得:∑ {q=2}^{40} δ²(q) → min {a,b}。然后,




















 291
291

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








