二叉树的结构和常见概念

节点的度：一个节点所有子节点的个数为该节点的度

树的度：树中的最大的节点的度

叶节点、终端节点：度为0的节点

非终端节点、分支节点：度不为0的节点

树的深度：树的层数

性质

1、深度为n的二叉树最多有个节点（n>0）

2、二叉树的第i层最多有个节点

3、总节点数=度数*度数对应节点数+1

遍历方式

 

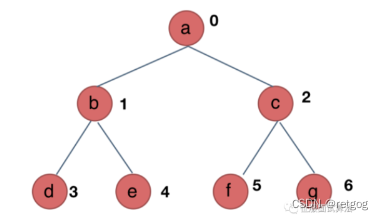
前序遍历（根左右）：0 1 3 4 2 5 6

中序遍历（左根右）：3 1 4 0 5 2 6

后序遍历（左右根）：3 4 1 5 6 2 0

前序和中序恢复二叉树

前序遍历（根左右）：0 1 3 4 2 5 6

中序遍历（左根右）：3 1 4 0 5 2 6

前序：0 为根（根左右）

左 3 1 4  左  0  右  5 2 6 右

0 1  1在左的集合，1为左子节点

                0

        1

0 1 3 3在左的集合，与根左右不符，更正根节点为1

1为根

《<左3左>1<右4右>》0  《 5 2 6 》

0 1 3 3在左的集合，3为左子节点

                0

        1

3

0 1 3 4 4在右的集合中，4为右子节点

                0

        1

3          4

0 1 3 4 2 2在《5 2 6》中，更正根节点为0

《<3>1<4>》0  《右 5 2 6 右》

0 1 3 4 2 2在右的集合中，2为右子节点，0已有左右结点，更正根节点为2

                0

        1                2

3          4        

《<3>1<4>》0  《 <左5> 2 <6右 >》

0 1 3 4 2 5 6 5在左集合，6在右集合，5为左节点，6为右结点

                0

        1                2

3          4        5        6

后序和中序恢复二叉树

中序遍历（左根右）：3 1 4 0 5 2 6

后序遍历（左右根）：3 4 1 5 6 2 0

后序：0为根（左右根）

左 3 1 4  左  0  右  5 2 6 右

2 0   2在左的集合，2为右子节点

                0

                        2

6 2 0 6在右的集合，与左右根不符，更正根节点为2

2为根

《3 1 4》0  《 <左5> 2 <右6> 》

6 2 0 6在右的集合，6为右子节点

                0

                        2

                                6

5 6 2 0 5在左的集合中，5为左子节点

                0

                        2

                  5            6

1 5 6 2 0 1在《3 1 4》中，更正根节点为0

《<左3>1<右4>》0  《<5> 2 <6>》

1 5 6 2 0 1在左的集合中，1为右子节点，0已有左右结点，更正根节点为1

                 0

        1                2

                    5            6

《<左3>1<右4>》0  《 <5> 2 <6 >》

3 4 1 5 6 2 0 4在右集合，3在左集合，4为右节点，3为左结点

                0

        1                2

3          4        5        6