<think>我们正在讨论
航电OJ（HD
OJ）2056题。根据用户需求，需要提供题目详情、解题思路和代码实现等。
但是，请注意，由于我无法直接访问外部数据库，我将基于我训练数据中的信息来回答。在我的知识截止日期（2023年）之前，
航电OJ 2056题是“Rectangles”，即计算两个矩形相交部分的面积。
题目描述：
给定两个矩形，每个矩形由两对点表示：第一个矩形的左下角点(x1,y1)和右上角点(x1',y1')，第二个矩形的左下角点(x2,y2)和右上角点(x2',y2')。注意，题目中给出的点可能是任意顺序，即不一定是左下角和右上角，但我们可以通过比较坐标来重新确定。
要求计算两个矩形重叠部分的面积（如果相交则输出面积，否则输出0.00）。
解题思路：
1. 首先，我们需要将给定的两个矩形的点转换为标准形式（即第一个点为左下角，第二个点为右上角）。可以通过取最小和最
大的x坐标以及最小和最
大的y坐标来得到。
但实际上，我们并不需要转换整个矩形，因为计算重叠部分只需要两个矩形各自在x轴和y轴上的投影区间。
2. 计算两个矩形在x轴上的投影区间的重叠长度。矩形1在x轴上的区间为[min(x1, x1'),
max(x1, x1')]，矩形2同理。然后计算两个区间重叠的长度。
重叠长度计算：设矩形1的x区间为[a1, a2]，矩形2的x区间为[b1, b2]（其中a1<=a2, b1<=b2），则重叠区间的左边界为
max(a1, b1)，右边界为min(a2, b2)。如果左边界小于右边界，则重叠长度为右边界减左边界，否则为0。
3. 同样计算y轴上的重叠长度。
4. 如果两个方向的重叠长度均
大于0，则重叠部分的面积为两个重叠长度的乘积；否则，面积为0。
5. 输出面积，保留两位小数。
注意：题目输入可能有多个测试用例。
代码实现（
C++）：
由于
航电OJ主要使用
C++，这里给出
C++代码示例：
```cpp
#include <iostream>
#include <iomanip>
#include <algorithm>
#include <cmath>
using namespace std;
int main() {
double x1, y1, x2, y2, x3, y3, x4, y4;
while (cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3 >> x4 >> y4) {
// 将第一个矩形转换为左下和右上
double rect1_left = min(x1, x2);
double rect1_right =
max(x1, x2);
double rect1_bot
tom = min(y1, y2);
double rect1_
top =
max(y1, y2);
// 第二个矩形同理
double rect2_left = min(x3, x4);
double rect2_right =
max(x3, x4);
double rect2_bot
tom = min(y3, y4);
double rect2_
top =
max(y3, y4);
// 计算x方向重叠：左边界取两个矩形左边的最
大值，右边界取两个矩形右边的最小值
double overlap_left =
max(rect1_left, rect2_left);
double overlap_right = min(rect1_right, rect2_right);
double x_overlap = overlap_right - overlap_left;
if (x_overlap < 0) x_overlap = 0;
// 计算y方向重叠：下边界取两个矩形底边的最
大值（注意：题目中坐标可能是任意方向，但我们已经转换为标准形式，底边就是最小y，顶边是最
大y）
double overlap_bot
tom =
max(rect1_bot
tom, rect2_bot
tom);
double overlap_
top = min(rect1_
top, rect2_
top);
double y_overlap = overlap_
top - overlap_bot
tom;
if (y_overlap < 0) y_overlap = 0;
double area = x_overlap * y_overlap;
cout << fixed << setprecision(2) << area << endl;
}
return 0;
}
```
但是，请注意：题目中给出的点可能是对角线上的任意两点，并不一定是左下角和右上角，所以我们需要将其标准化为左下角和右上角。上述代码中我们已经做了这一步。
此外，题目要求多组输入，所以使用while循环读取直到输入结束。
然而，有一个重要细节：题目中给出的两个矩形可能不是平行于坐标轴的？但根据题意，题目中给出的矩形都是边平行于坐标轴的（轴对齐矩形），所以我们可以这样计算。
如果题目中有非轴对齐的矩形，则需要更复杂的方法。但2056题明确是轴对齐矩形。
相关问题：
1. 如果矩形不是轴对齐的，如何计算两个矩形的重叠面积？
2. 如何计算多个矩形的重叠面积？
3. 在三维空间中，如何计算两个立方体的重叠体积？
如果用户需要其他语言的代码，请进一步说明。
注意：以上代码在
航电OJ上提交时，需要根据题目要求调整输入输出。题目链接：http
://acm.hdu.edu.cn/showproblem.php?pid=2056
</think>###
航电OJ 2056题：Rectangles
#### 题目描述
给定两个矩形，每个矩形用两对坐标表示（任意顺序）：
- 第一个矩形坐标：$(x_1, y_1), (x_2, y_2)$
- 第二个矩形坐标：$(x_3, y_3), (x_4, y_4)$
要求计算两个矩形重叠部分的面积（若不相交则输出 $0.00$）。
**输入格式**
多组测试数据，每组一行 $8$ 个实数：
$$x_1 \ y_1 \ x_2 \ y_2 \ x_3 \ y_3 \ x_4 \ y_4$$
**输出格式**
每组数据输出一行，保留两位小数。
---
#### 解题思路
1. **标准化矩形**
将每个矩形的坐标转换为标准形式（左下角 + 右上角）：
- 矩形 $A$：左下 $(A_{lx}, A_{ly})$，右上 $(A_{rx}, A_{ry})$
$$A_{lx} = \min(x_1, x_2), \quad A_{ly} = \min(y_1, y_2)$$
$$A_{rx} = \
max(x_1, x_2), \quad A_{ry} = \
max(y_1, y_2)$$
- 矩形 $B$：同理计算 $B_{lx}, B_{ly}, B_{rx}, B_{ry}$
2. **计算重叠区域**
- 重叠区域在 $x$ 轴上的投影：
$$\text{overlap}_x = \
max(0, \ \min(A_{rx}, B_{rx}) - \
max(A_{lx}, B_{lx}))$$
- 重叠区域在 $y$ 轴上的投影：
$$\text{overlap}_y = \
max(0, \ \min(A_{ry}, B_{ry}) - \
max(A_{ly}, B_{ly}))$$
- 重叠面积：
$$S = \text{overlap}_x \times \text{overlap}_y$$
3. **特例处理**
若 $\text{overlap}_x \leq 0$ 或 $\text{overlap}_y \leq 0$，则 $S = 0$。
---
#### 代码实现（
C++）
```cpp
#include <iostream>
#include <iomanip>
#include <algorithm>
using namespace std;
int main() {
double x1, y1, x2, y2, x3, y3, x4, y4;
while (cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3 >> x4 >> y4) {
// 标准化矩形A
double A_lx = min(x1, x2), A_ly = min(y1, y2);
double A_rx =
max(x1, x2), A_ry =
max(y1, y2);
// 标准化矩形B
double B_lx = min(x3, x4), B_ly = min(y3, y4);
double B_rx =
max(x3, x4), B_ry =
max(y3, y4);
// 计算重叠区域
double overlap_x =
max(0.0, min(A_rx, B_rx) -
max(A_lx, B_lx));
double overlap_y =
max(0.0, min(A_ry, B_ry) -
max(A_ly, B_ly));
double area = overlap_x * overlap_y;
// 输出结果
cout << fixed << setprecision(2) << area << endl;
}
return 0;
}
```
#### 关键点说明
- **坐标标准化**：无论输入坐标顺序如何，通过 $\min/\
max$ 统一为左下角+右上角。
- **重叠判断**：通过比较边界坐标确定投影区间，若区间无交集则面积为 $0$。
- **精度要求**：使用 `fixed << setprecision(2)` 保证输出保留两位小数[^1]。
---
### 相关问题
1. 如果矩形是三维的（立方体），如何计算重叠体积？
2. 如何判断多个矩形是否有公共重叠区域？
3. 若矩形可旋转（非轴对齐），如何计算重叠面积？
[^1]
: 航电OJ系统要求输出保留两位小数，需注意输出格式。
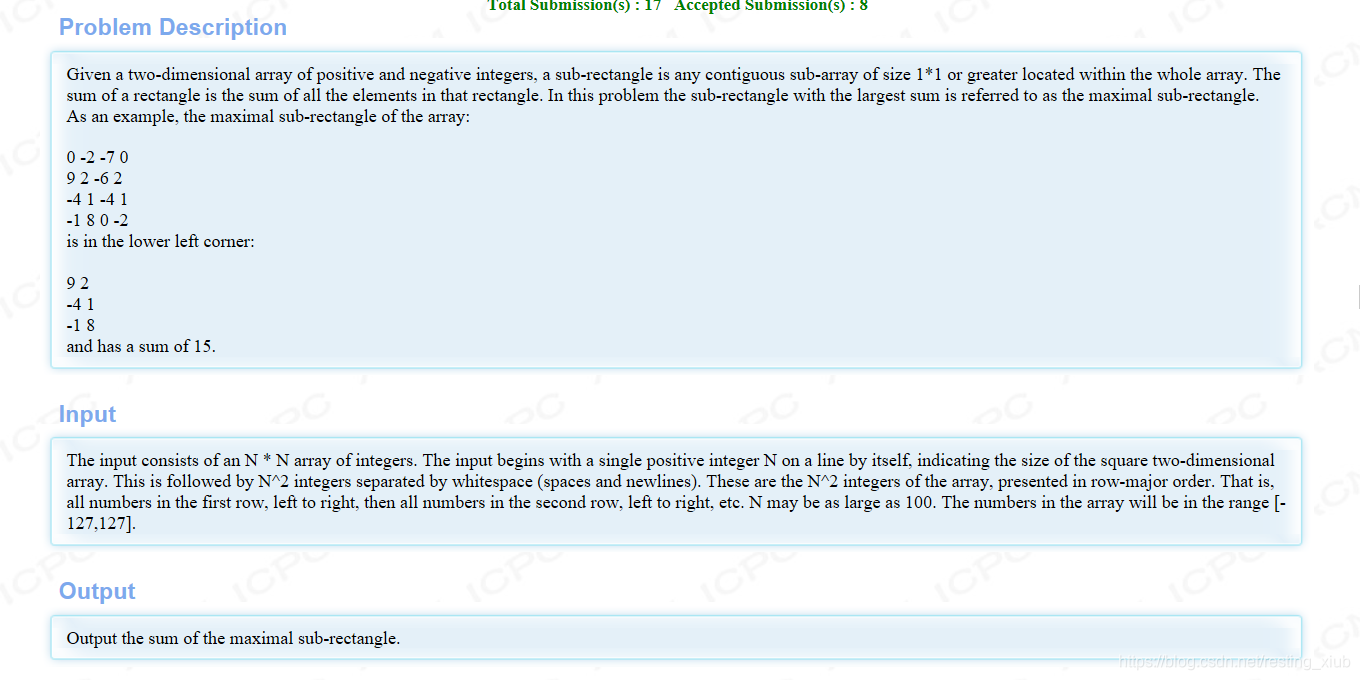
该博客介绍了如何使用动态规划解决一个寻找正方形块中最大矩形和的问题。代码示例展示了如何通过存储上一行的和来优化计算过程，避免暴力求解，从而找到最大值。在每一步中，矩形块的值会被更新以找到最大的和。
扫一扫
212
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
