基于GLCM与FCM的皮肤疾病分类

原创于 2025-10-14 12:32:05 发布 · 578 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#图像分类 #GLCM #FCM #皮肤疾病 #纹理特征

基于纹理和聚类的皮肤疾病分类

摘要

本文的主要目的是利用图像分类方法对皮肤病进行分类。为了分析图像的纹理，采用了统计方法灰度共生矩阵（GLCM）。灰度共生矩阵考虑了像素的空间关系，并通过计算具有特定值以及特定空间关系的像素对在图像中出现的频率来表征图像的纹理。本文的研究重点在于提取灰度共生矩阵的特征，包括对比度、相关性、同质性和能量。提出将模糊C均值聚类与灰度共生矩阵相结合，以减少皮肤病分类所需的时间。仿真结果表明，所提出的方法比单独使用灰度共生矩阵的方法更高效。

关键词 图像分类 GLCM Fuzzy c‐均值聚类皮肤疾病

1 引言

皮肤病是发展中国家和工业化国家中最常见的疾病之一。患有皮肤病的人生活压力较大，因为皮肤病在许多方面影响着他们的自信心和自尊心。

2013年，印度皮肤病的患病率为10%，受影响人口估计接近15.1亿。由于印度皮肤科医生的匮乏，这一情况进一步恶化[1]。在此背景下，医学影像在皮肤病识别中的快速决策方面发挥着重要作用。医学影像可用于揭示被皮肤遮蔽的内部结构，并用于疾病诊断与治疗。本文讨论了利用纹理和基于聚类的图像分类进行皮肤病检测的方法。

斯帕拉文加 [2]提出了一种基于纹理的方法，该方法通过模式识别的统计方法对皮肤颜色和粗糙度的差异进行定量评估。Abbadi 等人 [3]开发了一种基于灰度共生矩阵（GLCM）和皮肤颜色的皮肤病识别方法。本文使用 GLCM来测量相关性、对比度、能量和同质性等纹理特征，然后将模糊C均值聚类技术与通过GLCM提取的纹理特征结合使用。

本文的其余部分组织如下：第2节介绍所提出的方法。第3节讨论使用灰度共生矩阵（GLCM）提取图像特征。第4节介绍模糊C均值聚类。第5节展示仿真结果，第6节对全文进行总结。

2 提出的方法

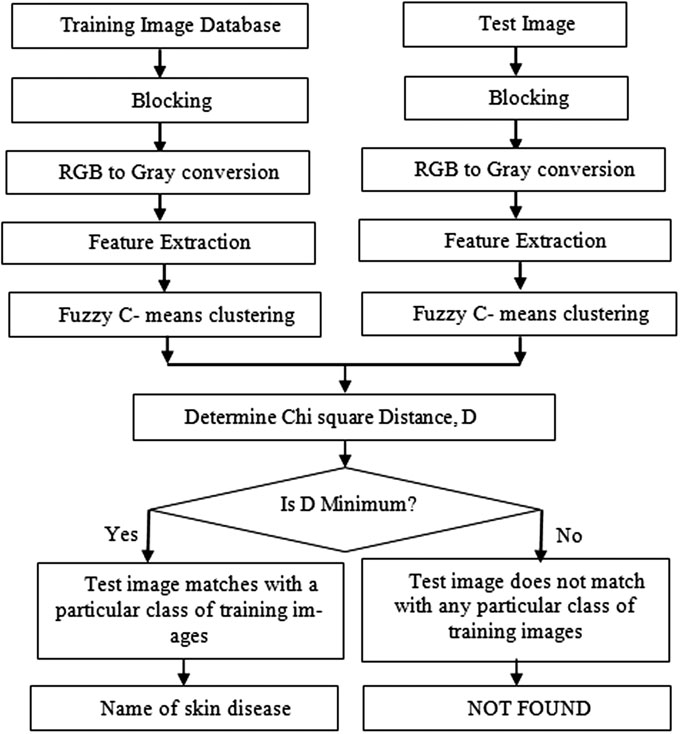
该方法通过分析图像集合中基于灰度共生矩阵的纹理特征，用于皮肤病类别的分类。该方法分为两个阶段：(a) 训练阶段和(b) 分类阶段。所提出方法的方法论如流程图（图1）所示。

我们考虑提取图像的四种纹理特征：相关性、对比度、同质性和能量。

在训练阶段，从给定的一组训练图像中提取纹理特征。在分类阶段，对给定的测试图像进行分割，然后提取上述纹理特征。接着，对从训练图像中获得的纹理特征应用模糊C均值聚类。然后，计算卡方距离用于皮肤病分类。

计算灰度共生矩阵并提取图像的纹理特征将在接下来的部分中讨论。

示意图0

3 灰度共生矩阵

灰度共生矩阵（GLCM）包含图像像素空间关系的二阶统计信息。纹理特征计算利用GLCM的内容来度量感兴趣像素处强度的变化情况[4]。在计算图像的GLCM时，考虑两个参数：偏移量和像素之间的距离d。其中，偏移量表示像素配对的方向。例如，0°偏移和d= 1表示水平相邻元素的配对。本文中，取d= 1，并考虑四个偏移量：0°、45°、90°和135°。45°、90°和135°偏移量分别通过右对角线元素、垂直向上元素和左对角线元素的配对获得。

3.1 图像的灰度共生矩阵

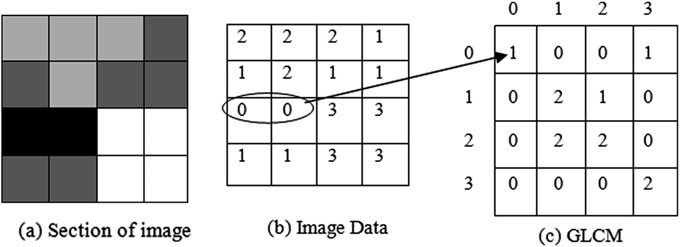
让我们考虑一个 4 × 4图像区域，该区域具有如图 2a 所示的 4个灰度级。图像数据和 0°偏移的灰度共生矩阵分别如图 2b、2c 所示。

令 G0°、G45°、G90° 和 G135° 分别表示偏移量为 0°、45°、90° 和 135° 的灰度共生矩阵。为了得到对称灰度共生矩阵，将原始灰度共生矩阵与其转置相加。然后通过将其除以所有元素之和获得归一化对称灰度共生矩阵。分别计算归一化对称灰度共生矩阵 N0°、N45°、N90° 和 N135°。

$$
N_{0^\circ} = \frac{1}{22}
\begin{bmatrix}
2 & 0 & 0 & 1 \
0 & 4 & 3 & 0 \
0 & 3 & 4 & 0 \
1 & 0 & 0 & 4 \
\end{bmatrix}
\quad
N_{45^\circ} = \frac{1}{18}
\begin{bmatrix}
0 & 2 & 1 & 0 \
2 & 2 & 1 & 2 \
1 & 1 & 2 & 0 \
0 & 2 & 0 & 2 \
\end{bmatrix}
$$

$$
N_{90^\circ} = \frac{1}{24}
\begin{bmatrix}
0 & 3 & 1 & 0 \
3 & 2 & 2 & 2 \
1 & 2 & 2 & 0 \
0 & 2 & 0 & 4 \
\end{bmatrix}
\quad
N_{135^\circ} = \frac{1}{20}
\begin{bmatrix}
0 & 2 & 0 & 1 \
2 & 0 & 2 & 1 \
0 & 2 & 2 & 2 \
1 & 1 & 2 & 2 \
\end{bmatrix}
$$

然后，从归一化对称灰度共生矩阵中提取给定图像的相关性、对比度、能量和同质性等纹理特征。

3.2 基于灰度共生矩阵的纹理度量

大多数纹理计算是对归一化的对称GLCM矩阵元素的加权平均值。

示意图1

对比度 (Con) 对比度是参考像素与其邻域像素之间强度或灰度级变化的度量。

$$
Con = \sum_{i,j=0}^{K} p_{i,j}(i-j)^2
$$

其中，$p_{i,j}$ 表示归一化对称灰度共生矩阵的元素 $(i, j)$，K 表示图像中的灰度级数，$(i−j)^2$ 表示权重。

相关性 (Cor) 它表示参考像素与其邻域像素的相关程度。其取值范围为 −1 到 1。−1 表示无相关性，1 表示完全相关。

$$
Cor = \sum_{i,j=0}^{K} \frac{(i - \mu_i)(j - \mu_j)p_{i,j}}{\sigma_i \sigma_j}
$$

$\mu_i, \mu_j$和$\sigma_i, \sigma_j$分别表示$p_{i,j}$的均值和标准差。

同质性（H） 同质性返回一个值，用于衡量灰度共生矩阵中元素分布相对于灰度共生矩阵对角线的接近程度。

$$
H = \sum_{i,j=1}^{k} \frac{p_{i,j}}{1 + |i-j|}
$$

能量 (E) 它衡量纹理的均匀性，即像素对的重复性。它能够检测纹理中的不规则性。其值简单地返回灰度共生矩阵中各元素平方的总和。

$$
E = \sum_{i,j=1}^{K} p^2_{i,j}
$$

3.3 基于灰度共生矩阵的分类

设$(N_{0^\circ}, N_{45^\circ}, N_{90^\circ}, N_{135^\circ}) {T_n}$表示训练图像$T_n$的归一化对称灰度共生矩阵集合；n = 1, 2,…, N。对于每组归一化对称灰度共生矩阵，计算上述四种纹理特征，并通过对每幅图像的各个特征集取平均值得到最终的纹理特征值。设$(Cor, Con, H, E) {T_n}$表示训练图像$T_n$的最终纹理特征值；n = 1, 2,…, N。

以类似方式，计算测试图像的平均纹理特征值。然后，通过计算训练图像与测试图像之间的卡方距离进行皮肤病分类。

4 基于模糊逻辑和灰度共生矩阵的皮肤疾病分类

在所有训练图像上实现灰度共生矩阵（GLCM），从中获取每幅训练图像的纹理特征。然后，对训练图像集的这些特征值应用模糊逻辑（C均值聚类）。

模糊C均值（FCM）聚类是一个迭代过程。首先生成初始的模糊划分矩阵，并计算初始的模糊聚类中心。在每次迭代过程中，更新聚类中心和隶属度点，并通过最小化目标函数来确定聚类的最佳位置。当达到最大迭代次数[6]时，该过程停止。通过这种方式，每个特征的N个聚类中心值形成一个集合，从而大幅降低计算复杂度。随后，根据训练类别的聚类中心与测试图像特征之间的相似性进行分类。

5 仿真结果

从www.dermnet.com收集了血管性水肿、日光性角化病和湿疹的皮肤病图像。它们被裁剪为 $100 \times 100$像素大小并转换为灰度图像，然后划分为训练集和测试图像集。

5.1 模糊逻辑的实现

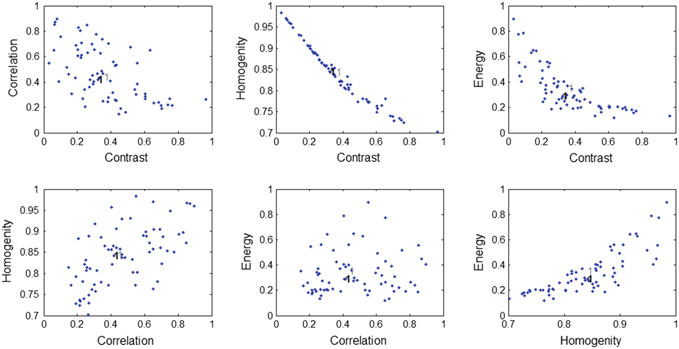
首先，对类别血管性水肿实施模糊逻辑，结果如图 3 所示，其中 1（加粗）表示聚类中心。从图 3 可以观察到，每个特征得到一个单一的值。对另外两个类别角化病和湿疹应用模糊C均值聚类，结果见表 1。

示意图2

5.2 皮肤病分类

使用卡方距离进行皮肤病分类。

卡方距离，
$$
d = \sum_{n=1}^{N} \frac{(S_n - M_m)^2}{S_n + M_m}；m = 1, 2, …
$$
$S_n$、$M_m$和$N$分别表示第$n$个训练图像、第$m$个测试图像和训练图像的数量。对于GLCM方法，$N$较大，而所提出的方法中$N = 1$。该过程对所有三个类别重复进行。

然后，类别，其距离最小，即为测试图像所属的类别。