基于LBP-Ferns的鲁棒人脸识别

基于LBP‐Ferns的鲁棒人脸识别特征提取

摘要

—大多数人脸识别（FR）系统首先从面部图像中提取判别性特征，然后进行分类。本文提出了一种用于表示人类面部特征的方法，以及一种使用正交线性判别分析（OLDA）的低维特征提取方法。所提特征依赖于局部二值模式来表示纹理信息，并利用随机蕨构建结构模型。通过将其特征向量进行拼接，该方法实现了对输入面部图像的高维描述。通常情况下，特征维度与其判别能力密切相关。然而，更高维度意味着更高的计算复杂度。因此，降维对于实际的人脸识别应用至关重要。本文采用OLDA降低提取特征的维度并提升判别性能。在具有代表性的人脸识别数据库上，所提方法相较于现有其他人脸识别方法表现出更高的识别率和较低的计算复杂度。此外，在包含伪装的面部图像数据库上，该算法也展现出优异的性能。

索引词

—人脸识别，特征提取，局部二值模式，随机蕨，正交线性判别分析。

I. 引言

在过去几十年中，人们提出了多种人脸识别（FR）方法[1]‐[7]。这些方法为各种应用提供了生物特征认证过程。与其他生物特征认证方法不同，人脸识别（FR）过程不需要在用户和设备之间进行物理接触。认证设备和目标生物特征对象。这对各种应用都有益处。在监控解决方案中，通过入口的人类会被摄像头（即闭路电视和视觉监控系统）捕捉，自动识别并记录到访客日志[8]‐[10]中。这一特定应用有助于安全问题。人脸识别还可应用于电子商务中的信用卡交易认证[11]。对于消费者而言，智能设备（如智能电视和智能手机）使用面部识别系统来解锁设备或区分用户[12],[13]。

尽管不断努力提高人脸识别的准确性，但在各种情况下识别人脸仍为计算机视觉研究带来了挑战。为了提升识别性能，重要的是在伪装、面部表情以及训练人脸图像样本不足等各种场景下，提取具有高区分性特征的人脸特征。此外，特征提取需要具备低复杂度以满足实际应用需求。

局部二值模式（LBP）是一种通过简单操作表示纹理信息的著名特征[14]。局部梯度模式（LGP）[15], 、局部方向数模式（LDN）[16], 、局部相位量化（LPQ）[17],和特征方向位平面（EDBP）[18]均为LBP特征的改进，它们均侧重于分析局部纹理信息。

然而，尽管基于LBP的特征在分析纹理信息方面表现出色，但传统的基于网格的采样方法[26]由于其低维度而缺乏足够的区分能力。通常情况下，特征维度与特征的区分能力密切相关[38]。最近，提出了一种基于随机投影的LBP特征提取方法，该方法利用随机采样技术[19]来提高识别性能。采用随机采样方法的人脸识别系统能够获取整体和局部信息，增加特征维度，并改善对面部特征的区分能力。

降维（DR）过程需要降低分类过程的计算复杂度。为此，采用基于子空间的降维方法，如主成分分析（PCA）[20],、线性判别分析（LDA）[21],和独立成分分析[22], ，将高维（HD）图像空间中的面部图像投影到低维（LD）子空间中。在低维子空间中，人脸可以更精确地表示，以消除上述变化、差异和/或噪声。注意，传统基于子空间的特征提取方法只能实现有限的人脸识别性能，因为它们无法提取用于分类的最具区分性的信息。由于传统方法提取的是整体面部特征，因此在降维过程中会稀释局部信息。

本文提出了一种具有高区分性的低维特征提取方法。所提特征通过融合局部二值模式（LBP）和随机蕨类（random ferns）[23]方法，同时表示局部纹理和结构信息。其中，LBP用于表示纹理信息；通过对LBP结果提取子集，该方法可表示人脸的局部特征。为了提高特征的区分能力，将LBP结果的子集与随机蕨类的采样技术相结合。本文将所提出的特征称为LBP‐fern特征。由于LBP‐fern特征基于LBP结果子集的直方图信息，因此生成的是高维特征。传统降维方法对此类高维特征效果不佳，因为它们需要足够大的样本集来分析高维特征。正交LDA（OLDA）被提出用于解决小样本问题[24], [25]。通过采用OLDA，所提出的特征提取方法生成低维特征向量，并提高了区分能力。

本文的其余部分组织如下。第二节介绍了传统特征。第三节详细阐述了所提特征提取方法。第四节展示了实验结果并进行了讨论，第五节对全文进行了总结。

II. 传统特征

A. 局部二值模式

局部二值模式（LBP）特征最初是为纹理分析而设计的。由于其对单调全局灰度变换具有不变性，且实现简单，因此在人脸识别（FR）中得到了广泛认可和应用[14]。LBP编码了中心像素与其邻域像素之间的二值模式，能够表示灰度图像的局部细节。

为了获得每个像素（x，y）处的局部二值模式映射，在以（x，y）为中心的3×3图像块上应用一个算子。更具体地说，该算子定义如下：

$$
\text{LBP}(x, y) = \sum_{n=0}^{7} t(i_c - i_n) \cdot 2^n
$$

其中，$i_c$ 和 $i_n$（n为= 0,…,7）分别表示中心像素及其对应的八个邻域像素的强度值。阈值函数$t(x)$定义为：

$$
t(x) =
\begin{cases}
1, & \text{if } x > 0 \
0, & \text{otherwise}
\end{cases}
$$

如图1(a)所示，从每个图像块中，LBP操作生成256个LBP数值之一，表示图像内部模式的特征。图1(b)显示了一幅输入图像，图1(c)显示了其LBP映射。

为了表示物体的结构信息，已提出多种基于局部二值模式（LBP）的方法。Timo等人提出了一种基于网格的LBP直方图方法[26]。在该方法中，面部图像被划分为多个区域，从中提取LBP特征分布，并连接成一个增强特征向量，用作人脸描述符。Ma等人提出的方法则随机提取特征位置和大小，然后拼接向量值[19]。这些特征提取方法将纹理信息描述为单独选取的区域，因此由于类似的眼部大小、鼻子形状以及其他区分个体的多样化面部特征，无法分析人脸的相对特征。

B. 随机蕨

为了提取相对面部特征，所提出的特征提取方法采用了随机蕨类采样技术。蕨类方法被提出用于描述输入图像[23]中的小图像块。图2展示了一个随机蕨类特征描述符的示例。每个蕨类f通过比较黑点的图像强度值和白点的位置值来计算。如图2的第一行和第二行所示，一个蕨类具有两种可能性，三个蕨类则具有八种可能性。蕨类特征是一种简单且快速的方法。

在图像块中进行特征提取。通过添加图像块样本，一组随机蕨可以以直方图的形式计算图像块的特征。由于其简单性和鲁棒性，随机蕨也可用于面部关键点定位。Xavier等人将此类随机蕨用作面部关键点检测器[27]。在人脸识别系统中应用随机蕨足以采用传统方法中的特征采样。为了提高判别性能，将面部图像中图像块的LBP直方图作为随机蕨中比较的依据。

III. 提出的方法

所提特征提取包括维度增加（DI）和降维（DR）部分，如图3所示。在DI部分中，对输入的面部图像进行基于LBP‐蕨类的特征计算。LBP‐Ferns方法的结果是将多个直方图连接成一个特征向量。在DI过程之后，降维方法对高维特征进行压缩。这些特征向量由多个直方图组成，其维度较高，并包含对人脸识别无判别性的不重要值。为解决此问题，采用OLDA以获得更具判别性的低维判别特征。OLDA同时降低了特征的维度和不重要值。以下小节将详细说明DI和DR过程及其意义。

A. DI：LBP-Ferns特征提取

通过选择输入LBP映射的子区域来构建用于提取LBP‐Ferns的直方图，因为从整张图像提取的直方图会破坏部分信息。图4展示了LBP子集直方图提取的一个示例。图4(a)和(b)中以矩形标示的右眼区域即为提取的目标区域。图4(c)和(d)显示了对应的裁剪后的图像。如图4(e)所示，子集直方图具有稀疏值，因为它表示整张人脸LBP映射的部分分解的数据。该直方图定义为 $h_s(r)$，其中s表示矩形核。此处，s由随机宽度和高度生成。r表示随机选择的坐标。

LBP‐fern特征$f$由两个直方图$h$得出，其定义为：

$$
f = h_{s}(r_1) - h_{s}(r_2)
$$

其中，$r_1$和$r_2$表示随机生成的坐标，用于避免核区域重复。如(3)式所示，核大小s应保持一致，以平衡直方图中LBP值的数量。通过两个直方图相减，所提特征能够同时获取纹理和结构信息，并描述个体面部的相对特征。相对特征表达了一个人的个体特征。例如，人眼的形状相似，但从眼睛和鼻子提取的相对特征在不同个体之间可能存在显著差异。

高维特征通过连接多个f生成。在所提特征中，高维特征由多个f的直方图组成。当f为单行向量时，LBP‐fern特征向量定义为：

$$
\mathbf{f} = [f_{s_1}, f_{s_2}, f_{s_3}, \ldots, f_{s_l}]^T
$$

其中s如上所述，是用于提取LBP直方图的矩形核。核的大小和长宽比随机生成，以表示面部图像中的各种特征。同时，s的坐标也被选择以避免每个核的重叠区域。每个蕨类$f$不应以相同大小和位置进行提取。l是LBP‐蕨特征池的最大索引。通过此操作，人脸识别系统获得具有高区分性的高维特征。图5展示了该过程。此处，每个$f$从两个LBP子集的直方图中提取。

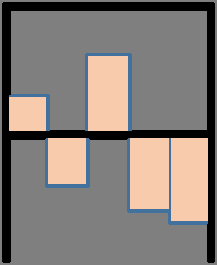
B. 降维：OLDA

用于高维特征的降维方法是减少人脸识别系统分类时间和存储使用的重要过程。经典LDA是一种有效的降维方法，可最大化类间距离与类内距离的比值。然而，经典LDA要求类内散射矩阵非奇异。在经典LDA框架下，由于训练样本数量相对于特征维度较少，经常出现样本不足问题，从而导致类内散射矩阵奇异。为克服这一问题，OLDA利用散射矩阵的同步对角化以及改进的目标函数（即经典LDA的平滑目标函数）来解决。将OLDA应用于LBP‐fern特征，所提特征提取方法不仅生成了有效的低维判别特征，而且实现了更高的区分能力。

考虑一组LBP‐fern特征向量，即$(f_k^c)$对于$c = 1, 2, 3, \ldots, C$和$k = 1, 2, 3, \ldots, N_c$，其中C和$N_c$分别为类别数量和第c类中的人脸图像数量。为了获得最优变换矩阵，假设每个类中的图像数量相等，即$N_c = N/C$，其中N为训练图像总数。在OLDA中，类内散射、类间散射和总散射矩阵分别定义如下：

$$
\mathbf{S}_w = \mathbf{H}_w \mathbf{H}_w^T, \quad \mathbf{S}_b = \mathbf{H}_b \mathbf{H}_b^T, \quad \mathbf{S}_t = \mathbf{H}_t \mathbf{H}_t^T
$$

其中

$$
\mathbf{H} w = [\mathbf{F}_1 - \boldsymbol{\mu}_1 \mathbf{e} {N/C}, \ldots, \mathbf{F} C - \boldsymbol{\mu}_C \mathbf{e} {N/C}]
$$
$$
\mathbf{H}_b = [\boldsymbol{\mu}_1 - \boldsymbol{\mu}, \ldots, \boldsymbol{\mu}_C - \boldsymbol{\mu}]
$$
$$
\mathbf{H}_t = \mathbf{F} - \boldsymbol{\mu} \mathbf{e}_N
$$

这里 $\mathbf{F}=[\mathbf{F} 1 , \mathbf{F}_2 ,…, \mathbf{F}_C]$, $\mathbf{F}_c=[f_1^{(c)}, f_2^{(c)}, …, f {N_c}^{(c)}]$, $\boldsymbol{\mu}_c$是类别c的平均特征向量，$\boldsymbol{\mu}$是所有特征向量的平均特征向量，而$\mathbf{e}_d \in \mathbb{R}^d$是一个列向量（所有元素都等于1）。

最优变换矩阵通过最大化以下目标函数来计算：

$$
\mathbf{W}^* = \arg\max_{\mathbf{W}} \frac{\text{Tr}(\mathbf{W}^T \mathbf{S}_b \mathbf{W})}{\text{Tr}(\mathbf{W}^T \mathbf{S}_t \mathbf{W})}
$$

其中$\text{Tr}(\cdot)$表示矩阵的迹，且$\mathbf{S}_t^+$表示矩阵$\mathbf{S}_t$的伪逆[28]。最终的低维特征向量可通过将输入的高维特征向量$f$投影到变换矩阵的向量空间上得到，如下所示：

$$
\mathbf{y} = \mathbf{W}^{*T} \mathbf{f}
$$

IV. 实验结果

在本节中，我们在代表性人脸数据库上进行了实验，以验证所提出的特征提取方法与协同表示分类（CRC）分类器[29]的性能。所使用的数据库包括AR[30], CMU PIE[31], LFW[32], 和扩展耶鲁B[33]。用于与提出的方法进行比较的方法包括LBP直方图[26], LPQ直方图[17], 以及CMM LBP[19]。需要注意的是，这些均为基于局部二值模式的部分特征方法。由于高度复杂的面部识别方法需要更多的系统资源，如电池、电力和计算能力，因此降低计算复杂度对于延长实际设备的使用时间至关重要。对计算复杂度的比较结果表明，提出的方法在消费类应用中具有较高的效率。

来自人脸数据库的图像首先被随机划分为用于训练和测试的两个子集，然后这些子集被用于所有评估，伪装评估除外（见第B.节）。为了确定产生最高识别率的特征数量，通过改变特征数量进行了评估。在每个数据库上的所有评估均执行五次，测量所得识别率的平均准确率作为提出的方法的性能。

A. 使用AR数据库进行多种面部表情评估

AR数据库[30]包含来自126个个体的4000多张正面图像。本次评估从AR数据库中选取了一个子集（仅包含光照和表情变化），其中包括50名男性和50名女性受试者。对于每个受试者，从AR数据库的第1次会话中随机选择7张图像用于训练，而第2次会话的另外7张图像用于测试。图像被裁剪为60 x 43像素。若干样本图像如图6所示。尽管该数据库呈现出具有挑战性的表情变化，但提出的方法实现了非常高的识别率，如表I所示，从而证明了其在光照和表情变化方面的鲁棒性。

特征	性能 (%)	# of 维度	备注
LBP直方图	95.9	2.07 × 10⁴	9×9 blocks
LPQ直方图	97.4	2.07 × 10⁴	9×9个模块
CMM LBP	97.7	700	-
提出的方法	99.4	99	300个特征

B. 基于AR数据库的伪装评估

本实验使用了AR数据库的一个子集。实验按照文献[34]中描述的实验设置进行了两次测试。图像被调整为165 × 120大小。图7(a)和(b)分别展示了佩戴太阳镜和围巾的测试图像示例。

对于伪装测试，使用了第1和第2阶段中800张图像（每个对象八个样本）的非遮挡正面视图，并包含各种面部表情用于训练，而分别带有太阳镜和围巾的200张图像子集（每阶段每个对象一个样本，中性表情）用于测试。所有子集均为手动选择。实验结果见表II和III。尽管维度较低，LBP‐Ferns仍优于其他三种方法。

特征	性能 (%)	# of 维度	备注
LBP直方图	98	2.07 × 10⁴	9×9 blocks
LPQ直方图	96.5	2.07 × 10⁴	9×9块
CMM LBP	93.5	1000	1000个特征
提出的方法	100	66	300个特征

表II AR伪装数据库（太阳镜组）上的性能

特征	性能 (%)	# of 维度	备注
LBP直方图	83.5	2.07 × 10⁴	9×9个块
LPQ直方图	69.5	2.07 × 10⁴	9×9个块
CMM LBP	59.5	2000	2000个特征
提出的方法	99.5	66	700个特征

表III AR化装数据库上的性能（SCARF集）

C. 基于CMU-PIE数据库的大样本评估

CMU‐PIE数据库[31]包含来自68个个体的41,368张人脸图像。这些图像在不同的姿态、光照模式和表情下采集。本实验使用了11,554张人脸图像（64×64分辨率），包含五种近正面姿态（C05、C07、C09、C27和C29）。图8展示了样本图像。在11,554张图像中，随机选择了3,514张图像用于训练，其余8,040张图像用于测试。表IV所示的结果表明，即使光照和适度姿态变化同时发生，提出的方法仍能实现最佳性能。

特征	性能 (%)	# of 维度	备注
LBP直方图	95.31	2.07 × 10⁴	9×9 blocks
LPQ直方图	95.43	2.07 × 10⁴	9×9 blocks
CMM LBP	94.73	3000	3000个特征
提出的方法	96.22	66	300个特征

表IV CMU‐PIE数据库上的性能

D. 使用LFW-a数据库的真实世界评估

LFW数据库[32]是一个非常近期的数据库，包含5,749个不同个体的图像，这些图像在光照、姿态、表情、错位、遮挡和图像质量方面具有很大差异。与上述数据库不同，该数据集是从网站收集而来的。这使得数据集更加真实。LFW‐a是使用商业人脸对齐软件[36]对齐后的LFW版本。如文献[37]所述，本实验共使用了157个受试者，每个受试者包含超过十个样本。对于每个受试者，随机选择五个样本用于训练，其余五个样用于测试。图像首先被裁剪至121×121，然后调整大小为32×32。图9展示了若干样本图像。

LBP‐Ferns在从700个特征中提取的157维上达到了最高识别率（63.3%）。如表V所示，其他方法的识别率均低于所提特征的结果。尽管LFW数据库的人脸识别难度相比其他数据库较高，提出的方法仍优于其他特征并实现了更好的性能。

特征	性能 (%)	# of 维度	备注
LBP直方图	37.3	1.25 × 10⁴	7×7 blocks
LPQ直方图	39.5	6.04 × 10⁴	5×5 blocks
CMM LBP	43.9	700	700个特征
提出的方法	63.3	157	700个特征

表V LFW数据库上的性能

E. 使用扩展Yale B数据库进行像素损坏和块遮挡评估

在人脸识别系统的实际应用场景中，由于摄像头噪声或其他环境网络流问题，可能会发生像素损坏或块遮挡。本节使用扩展Yale B数据库进行损坏和遮挡评估。该数据库包含38个受试者的2414张正面人脸图像。在这些实验中，图像在各种光照条件下生成后被裁剪并归一化为56×64像素图像。图10显示了原始样本图像。实验中，一半图像用于训练（即每个受试者约32张图像），另一半用于测试。随机划分数据库确保了实验结果不受训练和测试数据选择的影响。图11(a)和图11(b)分别展示了像素和块损坏的样本图像。

如表VI所示，对带有像素损坏的人脸图像在五个级别上进行了评估。LBP和LPQ直方图方法被划分为12×12个块，表现出最佳性能，而CMM LBP使用700个特征以达到最佳性能。基于直方图的方法具有3.68×10⁴维度，CMM LBP具有700个特征。

污染率	0%	10%	20%	30%	40%
LBP直方图	99.34	97.26	95.77	28.22	5.64
LPQ直方图	99.25	84.48	32.28	8.38	4.73
CMM LBP	99.8	98.6	94.5	86.06	67.63
提出的方法	99.67	99.67	99.67	96.18	67.72

表VI 耶鲁B数据库上的性能（像素损坏）

污染率	0%	10%	20%	30%	40%
LBP直方图	99.34	99.34	99.0	98.51	98.17
LPQ直方图	99.25	98.92	98.34	97.1	96.18
CMM LBP	99.8	98.3	94.9	84.7	69.2
提出的方法	99.67	99.67	99.67	99.50	99.50

表VII 耶鲁B数据库上的性能（块状遮挡）

F. OLDA评估

本节讨论了降维方法的评估。如第三节B部分所述，高维特征的降维方法是人脸识别系统中最重要的步骤之一。为了比较不同的降维方法，使用前述的LFW‐a数据库，并通过改变其维度，采用了主成分分析（PCA[20]）和线性判别分析（LDA[21]）进行评估。为了公平比较，特征数量固定为700。如表VIII所示，PCA在不同维度下的表现差异不大。在与OLDA相同的维度水平下，PCA的结果低了10.5%。即使PCA通过使用高维度来提升性能，OLDA仍表现出更优的结果。与LDA方法相比，OLDA在避免样本不足问题的同时，表现出相似的性能。这些结果证明了提出的方法的有效性和能力。

降维方法	特征数量	维度	性能 (%)
无降维	700	1.79×10⁵	58.2
PCA	700	157	52.8
PCA	700	300	57.1
PCA	700	500	59.9
LDA	700	157	62.1
OLDA（提出的方法）	700	157	63.3

表VIII 降维方法比较结果（LFW‐a数据库）

G. 计算复杂度

计算成本是实际人脸识别系统中的一个关键问题。在这些实验中，使用了四种人脸识别方法来验证提出的方法的适用性。这里使用了扩展Yale B数据库。实验设置采用了第四节E部分中描述的最佳性能所使用的相同参数。计算成本通过分离特征提取和比对时间来获得。特征提取过程在与存储的数据库进行比较之前仅执行一次。需要注意的是，人脸识别系统的存储使用取决于每个样本的维度。具有低维度特征的数据库需要较少的存储空间，并且具有较快的比对时间。这些方法在2.8 GHz CPU台式机上使用单线程实现用于人脸识别。

如表IX所示，提出的方法的计算时间最短。尽管提出的方法在所有方法中的特征提取时间最长，但由于其更好的识别性能，消耗的时间是可以接受的。

特征	维度	提取时间（毫秒）	比对时间（毫秒）
LBP直方图	3.68×10⁴	3	26
LPQ直方图	3.68×10⁴	2	25
CMM LBP	700	2	0.5
提出的方法	157	10	0.2

表IX 计算复杂度比较（扩展Yale B数据库）

V. 结论

本文提出了一种用于人脸识别的特征提取方法。通过在代表性的人脸识别数据库上进行实验，结果表明所提出的LBP‐fern特征在人脸识别应用中具有良好的区分能力。此外，OLDA有助于降维及其区分能力。该提出的方法在多种面部图像数据库上表现出优异的性能。在伪装和遮挡评估中，LBP‐Ferns对部分遮挡的人脸表现出鲁棒性。该提出的方法具有适中的计算复杂度和较高的识别率，适用于无需高性能处理器的消费电子产品。