Transformer position encoding 的细节

最新推荐文章于 2025-11-09 16:19:15 发布

原创

最新推荐文章于 2025-11-09 16:19:15 发布 · 307 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#transformer #深度学习 #人工智能

本文探讨了序列数据在自然语言处理中的特点，如长度变化、上下文关联和时序性，并介绍了RNN和Attention处理序列的方法及问题。重点讨论了Transformer中引入PositionEncoding解决位置关系的方法，以及为何选择10000作为参数的解释。

1. 序列处理的特点

在自然语言处理、语音识别和推荐系统当中，需要处理一类独特的数据: 序列。

序列数据的特点，决定了序列处理的特性。在常见的序列处理当中，我们面对的序列主要有以下几个特点。

特点 1: 序列的长度是变化的，长短不一。

特点 2: 序列当中的 Token不是独立同分布的。序列当中每个 token 的所携带的信息不仅与自身有关，也和这个Token 所处的位置有关(也就是我们常说的上下文信息)。

这里以情感分析为例子

I like this movie because it doesn’t have an overhead history. Positive
I don’t like this movie because it has an overhead history. Negative

在上面的例子当中，仅仅只是因为don‘t 位置的不同，就导致了这两个句子的情感标注一个是正向的，一个是负向的。也就是说，在自然语言处理场景中，词汇之间的顺序关系对语意十分重要。词汇的含义可以由其上下文表示。或者说:

我们认为一个Token的含义不仅由其本身表示，还和这个Token所在的场景有关系。

在自然语言处理领域，我们把Token所在的场景理解为上下文关系，而上下文关系通过词序来表示。可是对于其他场景而言，Token 所在的场景可能不仅仅是这个 Token 的上下文关系。例如推荐场景，可能还包括用户特征。

其实，如果回到真实的自然语言环境下。不同的人说出同一句话，可能表达的含义不同。也就是每个人其实都拥有自己的语言体系。 只是在自然语言处理里面，我们的数据集无法追溯用户和语言的场景，所以只能在大规模数据集下寻找通用的语言范式。

回到自然语言的场景下，如果只考虑序列之间的关系，问题就变成了: “需要通过什么方式来捕获序列当中 Token 之间的位置关系。”

特点 3: 序列的生成过程具备时序特性。也就是在一个序列当中，我们认为前面的 Token需要比后面的 Token 先被生成。

比如，在自然语言处理中生成一句话:

猫坐在帽子上。

这句话生成的时候，Token 的生成顺序是: [“猫”，“坐在”, “帽子”, “上”]。在生成这个序列的时候，生成 Token“猫”的时候，后面的Token是不被知道的。

为了满足上面所说的三个序列特点，在对序列进行建模的时候需要考虑以下几个问题:
(1) 如何处理长短不一的序列信息。
(2) 如何表示一个序列当中不同Token 之间的位置关系，也就是Token 和上下文之间的关系。
(3) 如何在生成过程中，防止序列信息的泄露。

2. 序列处理的方法

在 Transformer 出现以前，主流的处理序列的方法是 RNN 系列，以及 Attention。在这些方法里面也包括 LSTM，GRU 之类的优化结构。这里主要介绍一下 RNN和 Attention如何处理序列，以及在处理序列上的弊端。

2.1 RNN 对序列的处理

在介绍 RNN之前，我们首先来看一下自然语言处理当中的 Seq2Seq 模型架构。在 Seq2Seq模型架构当中，整个模型由两个部分组成:

Encoder 部分: 用来对输入的序列进行编码，得到最终的编码表示。
Decoder 部分: 对输入序列的编码表示做解码，等到预测的目标输出。

我们以中译英的翻译任务为例：

输入: 猫坐在帽子上。
输出: Cat sitting on hat.

Encoder 完成了对中文输入的编码得到 Context，Decoder 将编码后的序列解码成为英文。整体的结构图示如下:
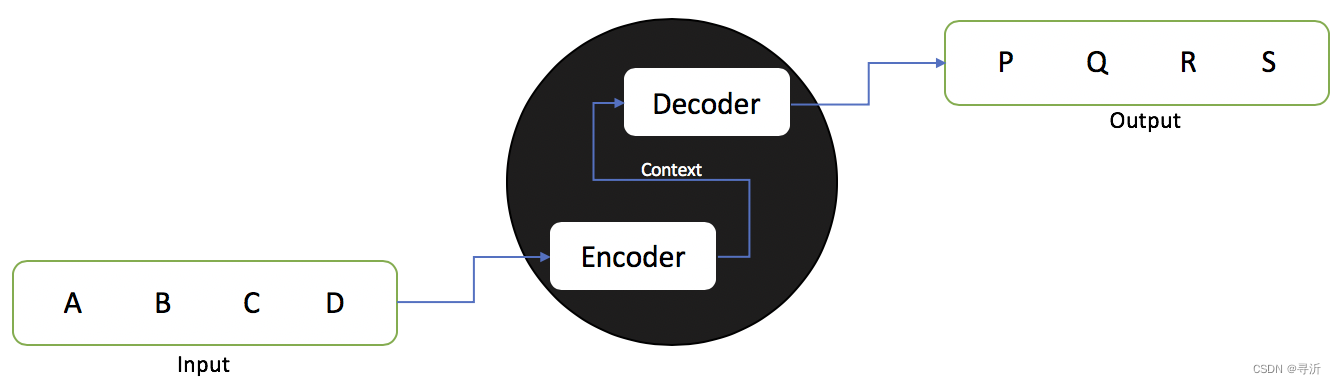
请添加图片描述

在 RNN 的实现当中，模型结构通过循环传递的 hidden state 来传递序列之间的信息从而捕获输入序列的位置关系。

如下图所示，每个输入在计算输出的时候，会有一个上游的 Hidden state 传入。同时会有一个 Hidden state输出。通过 Hidden State 的传递来实现序列之间位置关系的传递。

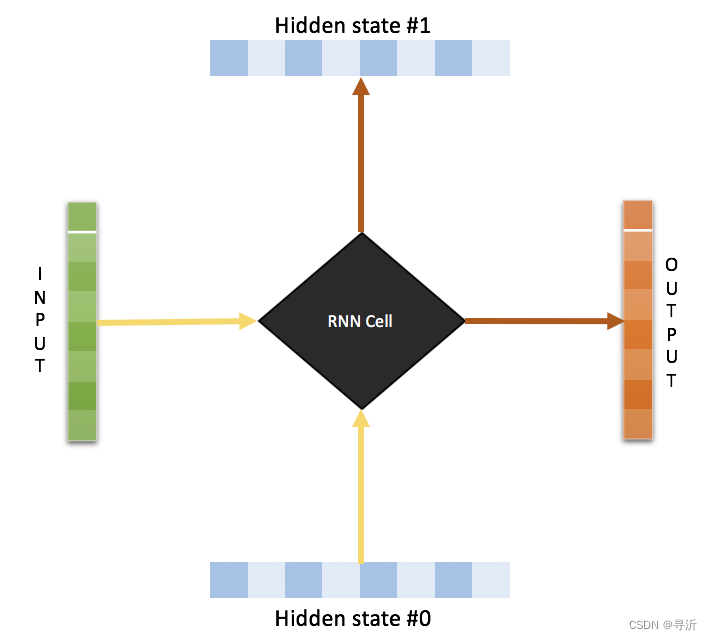
请添加图片描述

具体的实现可以参考代码:

def rnn_cell(rnn_input,state):  
    with tf.variable_scope('rnn_cell',reuse=True):  
        W = tf.get_variable('W', [n_classes + state_size, state_size])  
        b = tf.get_variable('b', [state_size], initializer=tf.constant_initializer(0.0))  
  
    # 定义rnn_cell具体的操作，这里使用的是最简单的rnn，不是LSTM  
    return tf.tanh(tf.matmul(tf.concat((rnn_input,state),1),W)+b)  
  
  
state = init_state  
rnn_outputs = []  
  
#循环num_steps次，即将一个序列输入RNN模型  
for rnn_input in rnn_inputs:  
    state = rnn_cell(rnn_input,state)  
    rnn_outputs.append(state)  
final_state = rnn_outputs[-1]

虽然，在处理序列信息方面，RNN 及其变种取得了一些进展，但是仍然存在以下一些问题:
问题 1: 由于 Hidden State一直在更新，如果循环更新的过程会丢失掉前面序列的信息，难以处理长序列。
问题 2: Hidden State 在网络中循环使用，导致梯度消失。
问题 3: 每个计算依赖于上一个 Hidden state 的输出，序列的每个 Token 需要串行计算。

2.2 Attention 对序列的处理

为了解决 RNN 在长序列上的缺陷，在 RNN 的基础上引入了 Attention 的机制。

可是，随着序列长度的增长，通过定长的 Hidden State向量表征整个序列的能力是有限的。此外，处理序列的时候，对不同位置的 Decoder对需要关注输入位置的重点也不一样。例如，在翻译任务中，翻译"I hate you"的时候，Decoder 翻译”我“和翻译”恨“注意力集中的位置可能不一样。

为了解决 RNN 对长序列处理的缺陷。在 RNN 的基础上，通过引入 Attention 机制来解决Decoder 过程的 Hidden State 权重分布问题。具体如下图所示：

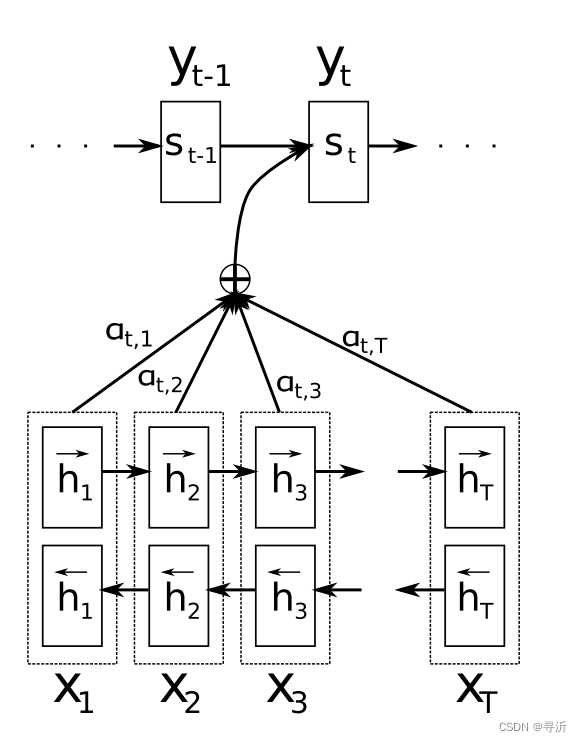
请添加图片描述

对于一个输入序列 $x_1, x_2, x_3, ... ,x_T]$ ，在Encoder 阶段生成了不同的Hidden State ，组成 Hidden State 序列表示为 $h_1, h_2, h_3,...,h_T]$ 。

在Decoder 阶段，如果需要计算 $t$ 位置的结果 $y_t$ ，RNN 结构是直接使用 Hidden state $s_{t-1}$ 做解码操作，得到最终的输出结果 $s_t$ 。

为了分别表示不同位置的 Hidden state 对解码出来的结果 $s_t$ 的影响，通过 Attention 机制计算输入 $s_{t-1}$ 对不同位置的Hidden state 的权重，表示为权重向量 $e_t$ ，然后通过 $e_t$ 对Hidden State 进行加权求和得到上下文编码向量 $c_t$