Transformer中的Position Encoding

原创已于 2022-03-15 15:32:15 修改 · 2.3k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#自然语言处理

于 2022-03-15 11:25:08 首次发布

NLP学习专栏收录该内容

1 篇文章

订阅专栏

主要记录一下Transformer中的Position Encoding，一些理解来自下面大佬的回答。

这里https://www.zhihu.com/question/347678607/answer/864217252

Transformer中的Position Encodeing：

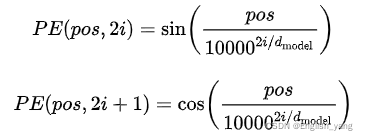
思考：

首先一点，模型中引入位置信息是有必要的，在NLP领域，词序乃至句序稍微的发生改变，整个含义就会发生改变，这种改变就应该体现在最终的Embedding上。在意识到位置信息（不论是相对位置还是绝对位置）的重要性后，就需要考虑如何将位置信息引入，即加入位置编码。一种最简单的方式就是计数，即使用：

$PE=pos=0,1,2,\cdots ,T-1$

当作文章中每个字的位置编码。这样做是存在问题的，整个序列没有上界。设想一段很长的(比如含有5000个字的)文本，最后一个字的位置编码非常大，会使得位置编码在于字本身嵌入合并之后数值上过大，出现合并后整体上的数值倾斜。另外就是位置编码过大可能导致与字本身嵌入合并之后的表示受位置编码的主导，对模型的结果产生干扰。

从上面的例子可以知道位置编码最好具有一定的值域范围，这样就有了新的想法：使用文本长度对每个位置作归一化，即：

$PE=pos/(T-1)$

这样固然使得所有位置编码都落入[0,1]的区间内，但是问题也是显著的：在较短的文本中紧紧相邻的两个字的位置编码差异会和长文本中间隔很远的两个字的位置编码差异一致。例如：

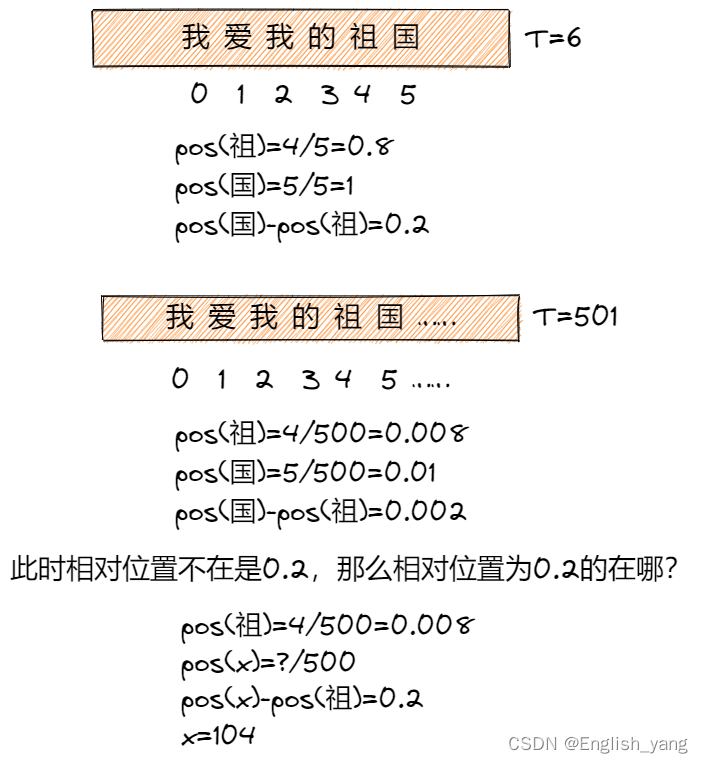
可以发现长文本和短文本中，相对位置都为0.2的，实际相聚的距离却十万八千里。这显然是不合适的，关注的位置信息，最核心的就是关注相对次序关系，尤其是上下文中的次序关系，如果使用这种方法，那么在长文本中相对次序关系会被「稀释」。

重新考虑一下对位置编码的要求：

需要体现同一单词在不同位置的区别。
需要体现一定的先后次序，并且在一定范围内的编码差异不应该依赖于文本的长度，具有一定的不变性。
需要有值域的范围限制。

这就考虑到周期函数，在前面的两种做法里面，为了体现某个字在句子中的绝对位置，使用的是一个单调的函数，使得任意后续的字符的位置编码都大于前面的字，如果放弃对绝对位置的追求，而是要求位置编码仅仅关注一定范围内的相对次序关系，那么使用一个sin/cos函数就是很好的选择。sin/cos函数周期变化规律非常稳定，所以编码具有一定的不变性。最简单的构造成如下形式即可：

$PE(pos)=sin(\frac{pos}{a})$

其中a用来调节位置编码函数的波长。但是这种做法太过于简单了，引入周期函数是为了解决上述第二种编码的问题，即复用位置编码的值域，但是上面的函数将值域映射到[-1,1]太单调，如果a比较大，相邻字符之间的差异就不够明显，如果a太小，在长文本中还是可能会有一些不同位置的字符编码一样。既然字符嵌入的维度是d，那么其实可以使用一个d维的向量来表示位置编码即[-1,1]^d，这个表示范围要远大于[-1,1]。

显然，在不同维度上应该用不同的函数操纵该位置编码，这样高维的表示空间才有价值。如可以为位置编码的每一个维度使用不同的a，或者交叉使用sin、cos函数，大概就这样，作者的方法就出来了：

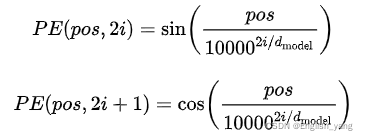
三角函数有如下公式：

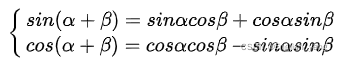
所以有：

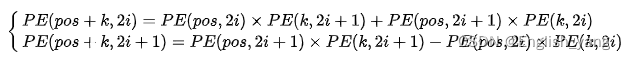
可以看出，对于pos+k位置的向量的某一维2i或者2i+1而言可以表示为pos位置和k位置向量2i和2i+1维的线性组合，这样的线性组合同样可以看作蕴含了相对位置信息。

代码实现：

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=512):
        super(PositionalEncoding, self).__init__()
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))#不论分段函数的哪一步，2*i都是偶数
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0).transpose(0, 1)
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + self.pe[:x.size(0), :]
        return x

其中 self.register_buffer('pe', pe)中的 register_buffer(）函数是Pytorch的一个函数，这条代码的作用是将pe这个tensor对象注册到模型的 buffers() 属性中，并命名为'pe'，在buffers()中的对象不会有梯度回传，但是模型会将这部分值存在state_dict中，相当于通常代码中的常量。在写法上其实等同于self.pe=pe。