在RNN里绕蒙圈

在上一篇文章《什么是seq2seq模型》中简单介绍了一下Seq2Seq。

在上次Seq2Seq的基础之上，我们聊一下RNN。

什么是RNN

在了解RNN的具体原理之前，我们先来看一下WIKI对RNN的介绍。

A recurrent neural network (RNN) is a class of artificial neural networks where connections between nodes form a directed graph along a temporal sequence. This allows it to exhibit temporal dynamic behavior. Derived from feedforward neural networks, RNNs can use their internal state (memory) to process variable length sequences of inputs.

递归神经网络(RNN)是一类人工神经网络，其中节点之间的连接沿着时间序列形成有向图。这允许它表现出时间动态行为。神经网络源自前馈神经网络，可以利用其内部状态来处理可变长度的输入序列。

所以神经网络的主要特点在于:

1. 能够构建时间序列，表现出时间动态行为。
2. 在前馈神经网络的基础上衍生而来
3. 处理可变长度的输入序列

从深度神经网络(DNN)说起

既然,RNN是从DNN衍生而来，那么我们就从DNN说起。

如下图所示，我们给出了一张DNN的网络结构图。

比如，我们在神经网络中需要处理一个这样的序列：

input：我是一个程序员。

output：I am a loser!

这个时候如果输入输出对是:

[(我， I), (是, am), (一个 a), (程序员, loser)]

这个时候input layer对应的输入分别为:

我, 是, 一个, 程序员

output layer对应的输出为:

I, am, a, loser

在这个时候,第一个输入输出对(我， I)和(是, am)这个输入输出对实际上存在序列关系，但是深度神经网络没有办法捕获这种关系。

这个时候，我们想是不是有一种方法能够根据记录前一个输入的状态，从而构建出有效的序列关系。

比如输入 “I” 该网络可以知道后面是 “am"用第一人称，输入"he” 知道用第三人称"is"。

RNN的基本结构及原理

在DNN模型结构的基础上，我们有了朴素的希望构建序列之间关系的想法之后，第一个反应就是:
我们能否通过一个hidden state在网络中隐性地传递下去，记录序列之间的关系。

基于此，我们得到一个基本的RNN模型中神经元的结构大概也就是下面这个亚子！

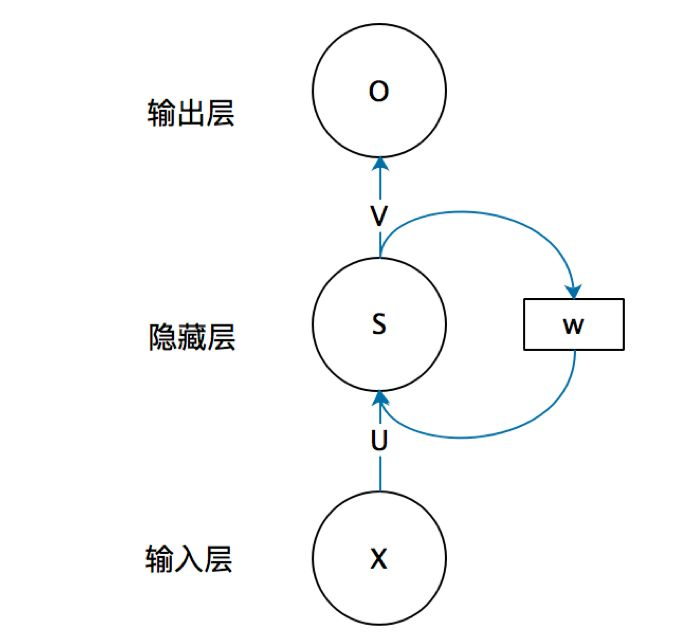
在上面的图中，我们的这个权重$w$用于记录模型训练过程中的序列状态。

还是以上面这个例子来说明为题,那么现在输入输出对就成了这个样子。

[((我, $w_0$)， (I, $w_1$)),

((是, $w_2$), (am, $w_3$)),

((一个, $w_3$), (a, $w_4$)),

((程序员, $w_4$), (loser, $w_5$))]

那么这单个神经元在时间维度上展开可以表示为如下方式：

看一下这图片，这曲线着身材是不是高端大气上档次。

RNN的数学描述

在上面的基础上，有了模型结构和基本思想之后，我们试图想办法用数学形式来定义和描述上面的模型结构。

毕竟，在程序员眼里没有办法用数学形式描述的东西都是耍流氓。

没有办法转化成0,1二进制的东西都是瞎扯淡，接下来要开始痛苦的历程了。

在《Recurrent Neural Networks cheatsheet》这样写道:

Recurrent neural networks are a strict superset of feedforward neural networks,
augmented by the inclusion of recurrent edges that span adjacent time steps,
introducing a notion of time to the model.

RNN是一个严格的前馈神经网络超集，增加了包含一条循环的边来连接临近的步长，从而在模型中引入时序的概念。

根据上面这段描述,我们可以简单知道的是：

• 在了解RNN之前，我们有必要先回顾一下feedforward nerual的神经网络结构和数学形式的描述。

• RNN是feedforward nerual的超集。那么在数学形式的描述上必然有很多相似的地方。

• RNN在feedforward nerual的基础上增加了一条递归边以记录时间序列。那么相比于前馈神经网络。怎么样描述那条递归边是一个非常重要的问题。

FNN 数学形式的描述

如图3所示，feedforward nerual network中单个神经元的构成如下。

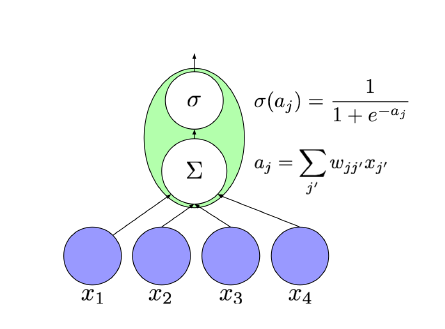
在图3中，给出了神经网络中的一个神经元$j$的，这个神经元的输入为$x_1,...,x_n$

通过这个神经元之后我们得到一个未激活值:
$$a_j=\sum _{j{}^{\prime }=0}^n{w}_{jj{}^{\prime }}{x}_{j{}^{\prime }}$$

在未激活值的基础上，采用softmax做激活函数得到激活值:
$$\sigma (a_j)=\frac{1}{1+e^{-a_j}}$$

RNN的数学形式描述

在上述网络的基础上，来看一下RNN的数学形式描述是什么样子的？

图4所示，是一个神经元的结构，那么这一层hidden layer我们需要通过什么样的方式来描述这一个Hidden Layer。

此外，在完成这个描述的基础上我们通过这个Hidden Layer完成前向传播和后向传播的模型训练。

我们依旧考虑在 $t$ 时刻的某一个神经元 $j$。

这个时候输入层输入的输入为向量 $x^t$，上一次输入对应的状态值为 $h^{t-1}$。

根据这些条件，我们计算当前状态值为：

$$h^t=\sigma (W_{hx}{x}^t+W_{hh}{h}^{t-1}+b_h)$$

$${\hat{y}}^t=softmax(W_{yh}{h}^t+b_y)$$

根据上述公式，我们完全可以计算得到这一次输入的对应的状态位输出 $h^t$ 和输出层输出 ${\hat{y}}^t$

其中不同参数的含义如下：

$W_{hx}$: 是输入和隐藏层之间的权重矩阵

$W_{hh}$: 是相邻步长上隐藏层之间的递归权重矩阵。

$W_{yh}$: 是隐藏层到输出层之间的权重

$b_h$: 是隐藏层便置量

$b_y$: 输出层偏置量。

为什么是这个样子

在前馈网络的基础上，我们得到了一个RNN神经元的数学表示形式如下：

$$h^t=\sigma (W_{hx}{x}^t+W_{hh}{h}^{t-1}+b_h)$$

$${\hat{y}}^t=softmax(W_{yh}{h}^t+b_y)$$

那么有一个灵魂问题，这个公式为什么是这个样子？

• 存在不一定合理
• 即使在合理的情况下也不一定合适

我们对比一下FNN和RNN单个神经元的描述形式会发现。

在FNN中对输出的计算描述成为的公式如下:

$$\sigma (a_j)=\frac{1}{1+e^{-a_j}}$$

在RNN中，对输出的计算公式描述方式为
$${\hat{y}}^t=softmax(W_{yh}{h}^t+b_y)$$

这两个公式在本质上没有太大的区别，而唯一的区别在于输入的不同。

在FNN中，我们将输入层给出的输入直接作为Input的结果参与到未激活值的计算，然后激活得到激活值。

在RNN中，神经网络和FNN中的区别之处在于原本直接作为输入的输入向量 $x$ 需要和隐藏状态hidden status做一下加权。

因此，在神经网络的训练过程中，我们认为这个时候的计算激活值的 ${\hat{y}}^t$ 不仅仅携带输入信息还携带了前面的信息。

参考资料

一文详解什么是RNN（循环神经网络）

Understanding RNN and LSTM

Recurrent Neural Networks cheatsheet

Deep Learning: Feed Forward Neural Networks (FFNNs)