LeetCode：516. 最长回文子序列

516 最长回文子序列
给定一个字符串s，找到其中最长的回文子序列。可以假设s的最大长度为1000。


示例 1:
输入:

“bbbab”

输出:

4

一个可能的最长回文子序列为 “bbbb”。
示例 2:
输入:

“cbbd”

输出:

2

一个可能的最长回文子序列为 “bb”。

1 解法1：递归式

根据上述题目的描述，我能够想到的最直接的解法就是：
对于字符串：

• 先判断一下这个字符串，是不是回文串，如果是直接返回长度。
• 如果不是，则将字符串每个字符去掉。
• 从新执行上述两个步骤

具体实现代码如下。

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        if self.longest(s) == True:
            return len(s)

        l = 0
        for i in range(len(s)):
            l = max(l,self.longestPalindromeSubseq(s[:i] + s[i+1:]))
        return l

    def longest(self, s:str) -> bool:
        l = True
        length = len(s)
        for i in range(length):
            if s[i] != s[length - 1 -i]:
                l = False
        return l

2 解法2：动态规划

在解法2中，我们将寻找最大回文子串的问题拆解为如下的问题：

• 对于一个字符串$s$，从索引为$i$到索引为$j$的区间内部最大回文子串，可以表述为公式：
  $f_{i,j}=\{\begin{array}{rlr}{f}_{i+1,j-1}+2& & s[i]==s[j]\\ max(f_{i+1,j},f_{i,j-1})& & s[i]!=s[j]\end{array}$

这样我们就将问题拆解成了一个子问题。基于上述结题思路，可以通过递归方法进行计算。
但是递归的方式么有办法记录中间结果。在下面的实现中，我们采用f来存储中间的计算结果。
在编写代码的过程中，我们可以把整个过程理解为如下的树状结构。

结构图 对于有ABCD四个字符的数组，这个数组一共可以组成的子串有上岸这么多种情况。 我们可以从前往后迭代，也可以从后往前迭代，去计算，0~n-1之间各个回文子串的大小，这里我们采用从前往后迭代的方式，具体如下。

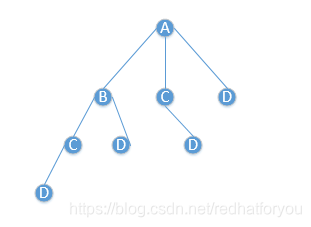
• 找到节点A，发现节点A前面没有节点，跳出循环
• 找到节点B，计算节点A到节点B之间的回文子串大小，并记录。
• 找到节点C，分别计算，节点A到节点C和节点B到节点C的回文子串大小，并记录。
• 依次类推，直到节点n，然后可以得到第一个节点到最后一个节点的回文子串大小。

在这个过程中，我们把之前的计算存储在数组f中避免了冗余的计算。

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        f = [[0 for i in range(n)] for i in range(n)]

        for i in range(n):
            f[i][i] = 1
            for j in range(i-1,-1,-1):
                if s[i] == s[j]:
                    f[j][i] = f[j+1][i-1] + 2
                else:
                    f[j][i] = max(f[j+1][i], f[j][i-1])
        return f[0][n-1]