交叉熵三连(3)——交叉熵及其使用

相关文章：
交叉熵三连(1)——信息熵
交叉熵三连(2)——KL散度(相对熵)
交叉熵三连(3)——交叉熵及其使用
  在神经网络中，我们经常使用交叉熵做多分类问题和二分类的损失函数，在通过前面的两篇文章我们了解了信息熵和相对熵(KL散度)的定义和计算方式以及相关的基础知识。在这篇文章中，会主要总结一下关于交叉熵的内容。

  一来因为刚开始写博客的缘故，二来所学的知识有限。博客中有很大的篇幅其实是拼凑得来，可能会跟参考资料有大量的重复之处，自己深入的理解相对会少一些，权且是学习的记录。

  如果博客中能有帮助到大家的地方，我很开心，如果大家有什么疑问也可以和我沟通讨论，有错误的地方欢迎大家批评指正我尽量第一时间修改，联系方式在签名中给出。

1 交叉熵的定义

交叉熵：表示当基于一个“非自然”分布$Q$对真实分布$P$进行编码时，在事件集合中唯一标识一个事件所需要的平均$bit$数。
对于给定的两个概率分布$P$和概率分布$Q$对应的交叉熵的定义如下：
$$H(P,Q)=E_P[-logq]=H(P)+D{L}_{KL}(P||Q)$$
其中$H(P)$是$P$的熵，$D{L}_{KL}(P||Q)$是相对熵，那么对于离散分布而言：
$$H(P,Q)=-\sum _{x}P(x)logQ(x)$$

2 交叉熵的计算

2.1 二分类交叉熵

在二分类问题中，交叉熵的计算方式如下所示：
$$L=-[y\cdot log(p)+(1-y)\cdot log(1-p)]$$
其中：
$y$:表示样本 $label$ 的值，如果 $label$ 正类$y=1$，负类$y=0$
$p$:表示样本预测为正的概率

如果上述公式没有办法直接理解，那么根据交叉熵计算公式
$$H(P,Q)=-\sum _{x}P(x)logQ(x)$$
对于二分类问题，上述公式转化为如下形式：
H ( P , Q ) = − ∑ x ∈ { 0 , 1 } P ( x )    l o g    Q ( x ) = − ( P ( x 0 )    l o g    Q ( x 0 ) + P ( x 1 )    l o g    Q ( x 1 ) ) H(P,Q) =- \sum_{x\in\{0,1\}}P(x)\;log\;Q(x) \\ =-(P(x_0) \;log\;Q(x_0) + P(x_1)\;log\;Q(x_1)) H(P,Q)=−x∈{0,1}∑​P(x)logQ(x)=−(P(x0​)logQ(x0​)+P(x1​)logQ(x1​))
令$P(x_0)=y$，并且$Q(x_0)=q$，那么$P(x_1)=1-y$，且$Q(x_1)=1-q$
上述公式简化为如下所示
$$L=-[y\cdot log(p)+(1-y)\cdot log(1-p)]$$

如果$x_0$表示正样本的话，$y$ 的值等于正样本真实的概率等于 $label$ 的值, $q$ 的值表示为正样本的预测概率。

2.2 多分类交叉熵

对于多分类问题的交叉熵在二分类问题上扩展后的具体计算公式如下：
$$L=-\sum _{c=1}^M{y}_{c}log(p_c)$$
在上述公式中:
$M$:表示类别的数量
$y_c$:当前观测样本属于类 $c$的时候$y_c=1$，否则 $y_c=0$
$p_c$:当前观测样本预测到类别$c$的概率

3 为什么是交叉熵

3.1 为什么不是分类错误率

  很多人一开始理解损失函数就是分类错误率，我刚开始的时候也是这么认为的，分类错误率的计算公式如下:
$$R_e=\frac{C_e}{C_a}$$
  在上述公式中:
$R_e$:表示分类错误率
$C_e$:表示分类错的样本个数
$C_a$:表示所有的样本的个数

  在参考的文章中给出了一张样例表，样例表中给出了三组民意选举预测的结果和对应的标签。

• 模型1

计算结果	标签	是否正确
0.3 0.3 0.4	0 0 1(民主党)	yes
0.3 0.4 0.3	0 1 0 (共和党)	yes
0.1 0.2 0.7	1 0 0 (其他)	no

  在三种结果中选民1和选民2的预测以微弱的优势获胜，选民3的民意预测结果彻底错误，计算得到的分类错误率为：
$$R_e=\frac{1}{3}$$

• 模型2

计算结果	标签	是否正确
0.1 0.2 0.7	0 0 1(民主党)	yes
0.1 0.7 0.2	0 1 0 (共和党)	yes
0.3 0.4 0.3	1 0 0 (其他)	no

  在模型2中给出了另外一组假设数据，在这组假设数据中选民1和选民2的判断非常准确，选民3以轻微的概率优势判错，分类错误率计算为:
$$R_e=\frac{1}{3}$$
  在上面给出的模型实例中，虽然错误率相等但是从三组样本最后预测的分类概率看，模型2具有相对明显的优势，但是通过分类错误率没有办法较准确的评估。

---

   接下来我们分析一下使用交叉熵计算得到$loss$的值，在计算过程中采用$ACE$(Average cross-entropy error)来计算平均交叉熵，根据多分类问题计算交叉熵计算公式得：

• 模型1
  $$1:-(ln(0.3)\ast 0+ln(0.3)\ast 0+ln(0.4)\ast 1)=-ln(0.4)$$
  $$2:-(ln(0.3)\ast 0+ln(0.4)\ast 1+ln(0.3)\ast 0)=-ln(0.4)$$
  $$3:-(ln(0.1)\ast 1+ln(0.2)\ast 0+ln(0.7)\ast 0)=-ln(0.1)$$
  $$L=\frac{-(ln(0.4)+ln(0.4)+ln(0.1))}{3}=1.38$$
• 模型2：
  $$L=\frac{-(ln(0.7)+ln(0.7)+ln(0.3))}{3}=0.64$$

结论:

• ACE结果准确体现了模型2的效果优于模型1
• cross-entropy 更清晰的描述了真实分布的数据和预测数据的距离

3.2 为什么不是均方误差(MSE)

  接下来我们看看使用均方误差作为损失函数是个什么样的效果。首先根据3.1节中给出的数据，我们计算均方误差如下。

• 模型1
  $$1:(0.3-0{)}^2+(0.3-0{)}^2+(0.4-1{)}^2=0.54$$
  $$2:(0.3-0{)}^2+(0.4-1{)}^2+(0.3-0{)}^2=0.54$$
  $$3:(0.1-1{)}^2+(0.2-0{)}^2+(0.7-0{)}^2=1.34$$
  $$L=\frac{(0.54+0.54+1.34)}{3}$$

• 模型2
  $$L=\frac{(0.14+0.14+0.74)}{3}$$

  根据MSE的计算结果可知，使用MSE好像也能很好的评估模型1和模型2的效果，为什么不用MSE来作为损失函数去优化整个模型的训练结果呢？主要原因有两个：

• 原因1：函数的单调性 。采用MSE做为损失函数的情况下，损失函数是非凸函数具有很多极值点，容易陷入局部最优解。
• 原因2：计算的简洁性。 使用均方误差作为loss函数的时候求导结果比较复杂运算量会比较大，使用交叉熵计算结果的时候比较简单，反向误差的计算比较简单。

3.2.1 求导过程简洁性对比

  在分类问题中最后计算每一个类的概率的时候，采用$softmax$计算映射到每一个类的概率，$softmax$对应的具体公式如下所示。
$$softmax(x{)}_i=\frac{exp(x_i)}{{\sum }_{j}exp(x_j)}$$
  采用MSE计算loss，输出的曲线是波动的，损失函数表现的不是凸函数，有很多局部的极值点，这种情况下难以得到最优解，使用交叉熵函数能够保证在区间内的单调性。
  以下我们以二分类为例分别证明MSE损失函数和交叉熵损失函数的单调性，具体的证明情况如下：

1. 交叉熵损失函数的求导过程
  在二分类问题钟交叉熵损失的计算过程如下。

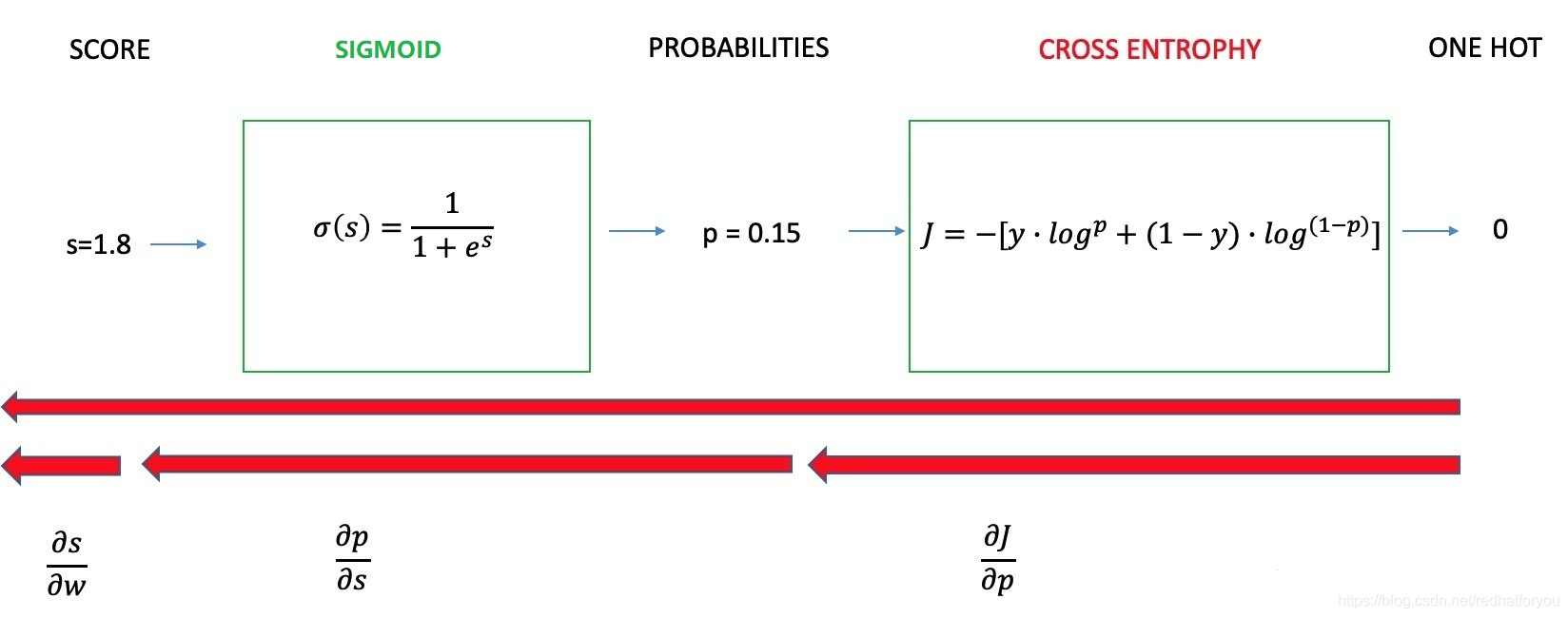
  我们简单的假设$score$是线性函数输入的结果，假设参数$w$和得分$s$的计算公式为:
$$s=w_i\cdot x_i+b_i$$
根据上述过程，二分类问题正向的$L$计算分为三个阶段

• score得分的计算
  $$s=w_i\cdot x_i+b_i$$
• sigmoid计算公式
  $$p_i=\frac{e^{s_i}}{1+e^{s_i}}$$
• 交叉熵损失的计算
  $$L=-[y\cdot log{p}_i+(1-y)\cdot log(1-p_i)]$$
  根据损失函数的计算过程，我们需要反向地计算偏导$\frac{\partial L}{\partial w_i}$，与上面相反的，我们把求导过程也分为三个部分。
  
  
• $\frac{\partial L}{\partial p_i}$ 导数的计算
  $$\frac{\partial L}{\partial p_i}=\frac{\partial (-[y\cdot log{p}_i+(1-y)\cdot log(1-p_i)])}{\partial p_i}=-\frac{y}{p_i}+\frac{1-y}{1-p_i}$$

• $\frac{\partial p_i}{\partial s_i}$ 导数的计算
  $$p_i=\sigma (s_i)=\frac{e^{s_i}}{1+e^{s_i}}$$
  令：
  $$h(x)=1+e^x$$
  $$g(x)=e^x$$
  那么有：
  $$\begin{gathered} \frac{\partial p}{\partial s_i}=(\frac{g(s_i)}{h(s_i)}{)}^{\prime }=\frac{h(s_i)g^{\prime }(s_i)-g(s_i)h^{\prime }(s_i)}{h^2(s_i)} \\ =\frac{(1+e^{s_i})(e^{s_i}{)}^{\prime }-e^{s_i}(1+e^{s_i}{)}^{\prime }}{(1+e^{s_i}{)}^2} \\ =\frac{(1+e^{s_i})\cdot e^{s_i}-e^{s_i}\cdot e^{s_i}}{(1+e^{s_i}{)}^2} \\ =\frac{e^{s_i}}{(1+e^{s_i}{)}^2} \\ =\frac{e^{s_i}}{1+e^{s_i}}\cdot \frac{1}{1+e^{s_i}} \\ =\frac{e^{s_i}}{1+e^{s_i}}\cdot [1-\frac{e^{s_i}}{1+e^{s_i}}] \\ =\sigma (s_i)\cdot (1-\sigma (s_i)) \end{gathered}$$
  
  

• $\frac{\partial s_i}{\partial w_i}$ 导数的计算
  $$\frac{\partial s}{\partial w_i}=x_i$$

  最终，我们计算$\frac{\partial L}{\partial w_i}$的结果得到
$$\begin{gathered} \frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial p_i}\cdot \frac{\partial p_i}{\partial s_i}\cdot \frac{\partial s_i}{\partial w_i} \\ =[-\frac{y}{p_i}+\frac{1-y}{1-p_i}]\cdot \sigma (s_i)\cdot [1-\sigma (s_i)]\cdot x_i \\ =[-\frac{y}{\sigma (s_i)}+\frac{1-y}{1-\sigma (s_i)}]\cdot \sigma (s_i)\cdot [1-\sigma (s_i)]\cdot x_i \\ =[-y+y\cdot \sigma (s_i)+\sigma (s_i)-y\cdot \sigma (s_i)]\cdot x_i \\ =[\sigma (s_i)-y]\cdot x_i \end{gathered}$$
2. MSE损失函数的求导过程
  在使用MSE作为损失函数的时候，计算最终的loss值的大小前两个步骤与使用交叉熵的计算过程相同，第三个阶段计算公式如下:
$$L=(y-p_i{)}^2$$
反向求导过程：
$$\frac{\partial L}{\partial p_i}=-2\cdot y+2\cdot p_i$$
我们把常数去掉
$$\frac{\partial L}{\partial p_i}=-y+p_i$$
那么对应的$\frac{\partial L}{\partial w_i}$计算的过程如下：
$$\begin{gathered} \frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial p_i}\cdot \frac{\partial p_i}{\partial s_i}\cdot \frac{\partial s_i}{\partial w_i} \\ =(-y+p_i)\cdot \sigma (s_i)\cdot [1-\sigma (s_i)]\cdot x_i \\ =[-y\cdot \sigma (s_i)+\sigma (s_i)\cdot \sigma (s_i)]\cdot [1-\sigma (s_i)]\cdot x_i \end{gathered}$$

对比权重更新的导数公式，使用交叉熵作为损失函数最后得到导数公式更简洁偏于计算。

3.2.2 损失函数的是否为凸函数

  关于损失函数是否为凸函数的问题，我理解的还不是很深刻，常读常新。等我有了进一步理解再来增加更新这一部分的内容，或者是新起一篇博客再具体说一下凸函数优化和非凸优化以及是不是凸函数的问题吧！

  如果要进一步探究这个问题，大家可以参考以下几个资料：

【机器学习基础】交叉熵（cross entropy）损失函数是凸函数吗？

二元分类为什么不能用MSE做为损失函数？

不理解为什么分类问题的代价函数是交叉熵而不是误差平方，为什么逻辑回归要配一个sigmod函数？

  感觉越看越觉得搞机器学习跟炒股一样是玄学不成？刚开始还觉得对交叉熵理解清楚了，越看越迷糊多问几个为什么就彻底迷糊了，只能把自己稍微觉得有点道理，或者是认同并且可以理解的罗列出来。知之为知之，不知为不知，上下求索吧~
  如果有后续，我后续有新的理解我再写交叉熵后传吧！！！
  欢迎大家讨论。

3.3 为什么不是相对熵(KL散度)

  交叉熵系列的学习和介绍中，我写了三篇博客分别是介绍了信息熵、KL散度(相对熵)和交叉熵。根据前面介绍的内容KL散度可以用来衡量数据的真实分布和预测分布的距离，那么为什么不用KL散度去衡量真实样本和预测结果之间的差距，作为损失函数。
  这里我们回顾一下交叉熵的定义：
$$H(P,Q)=E_P[-logq]=H(P)+D{L}_{KL}(P||Q)$$
  对于$H(P,Q)$表示用预测分布$Q$去编码真实分布$P$所需要的平均$bits$数。因为对于模型的训练过程来说真实分布通过样本的数据分布来估计,所以分布$P$是固定的，那么$H(P)$的值是一个常量。那么：

• 在模型训练的过程中，通过交叉熵和KL散度去评估预测分布和真实分布的距离具有相同的效果。

  接下来我们再回顾一下KL散度的计算公式和交叉熵的计算公式。

KL散度计算公式
$$D{L}_{KL}=\sum _{i}P(x_i)log(P(x_i))-\sum _{i}P(x_i)log(Q(x_i))$$
交叉熵的计算公式
$$C_e=-\sum _{i}P(x_i)log(Q(x_i))$$

根据上述公式对比，使用交叉熵用作损失函数评估真实分布和预测分布距离的时候具有明显的计算上的简洁性。

4 TensorFlow提供的交叉熵接口

tf.nn.sigmoid_cross_entropy_with_logits
tf.nn.softmax_cross_entropy_with_logits
tf.nn.sparse_softmax_cross_entropy_with_logits
tf.nn.weighted_cross_entropy_with_logits

5 参考资料

【1】维基百科 · 交叉熵
【2】知乎 · 损失函数 - 交叉熵损失函数
【3】神经网络的分类模型 LOSS 函数为什么要用 CROSS ENTROPY
【4】知乎 · 为什么用交叉熵做损失函数
【5】github · 03.2-交叉熵损失函数
【6】Tensorflow 中文社区