网络流问题

前言

讲的是在一个有向图形成的网络中，我们需要找到其中的最大流量。
这个问题是实际上也是有很大用处的。

我们先描述一下问题：
输入一个有向加权图（权值为这条边的最大容量），这个图有起点和终点，起点只有出度，终点只有入度，我们需要计算出从起点到终点的最大流量。
举例：

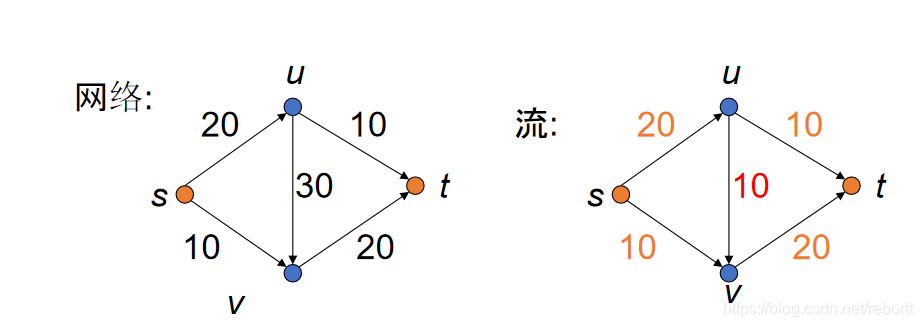
在这个问题中，我们的最大流量为30。

解决办法

先尝试找一条路径吧：
就按照上面的例子，这里我们使用深度优先的树搜索方式，找到的路径为s->u->v->t。
（这里面不需要看权值，只是随便找一个。如果不知道树搜索的原理，这里有博客。）

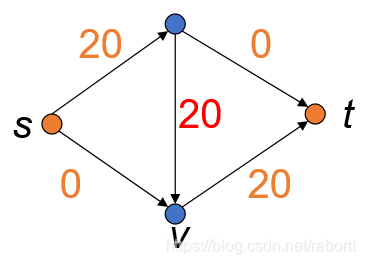
这时我们想要再重新找出一条路径，发现就没有了！（我们只有u->v的边）
很明显，因为我们最开始的选择不合适，导致做不出来了。

我们当然可以通过寻找一种贪心的方式来每一次直接确定最优解，但是这很难，这里给另外一种方式：
在取完路径之后，我们给出一个新的概念——余图。
在网络图和流图的基础上，我们给出几个关键点：

1. 在网络图中我们可以将流图用掉的部分反向，通过再利用进行抵消。
   （比如图中的u->v，我们只需要10，但是最开始就用了20，如果将其反过来，我们就能重复利用，找到更优解）
2. 网络流的边是可以拆分的，比如一个a到b的路径我们只用了一部分，就需要将路径拆成两部分，将其中一部分反向。

余图：
因为s到u的20都用了，所以直接反向；u到v的只用了20，我们将这部分反向，两条线放在那就行。
（别看两个方向相反就直接上去抵消了，反而会有影响）

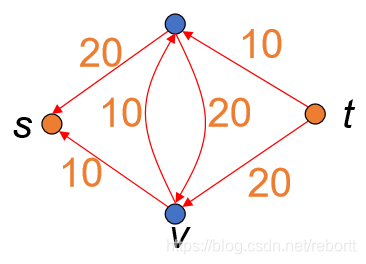
将余图当成新的网络图，再次得到一个流图，然后求余图……直到我们再也找不到从起始点到终点的路径，算法就可以结束了。

原理其实就是我们本来是可以不用这么多的，或者说是可以进行分流（一个流在一个顶点分为两个流）
但是深度优先不能实现，所以我们通过反向的方式来保证边能被重复使用，进行抵消。

另一个例子

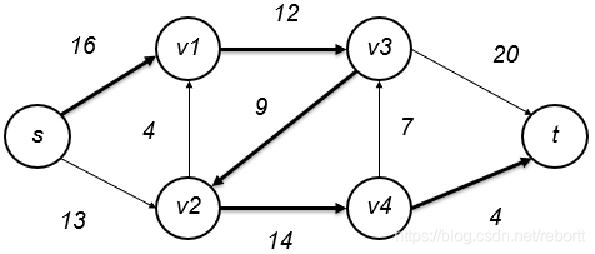
接下来我们好好分析一下。
先选s - 1 - 3 - 2 - 4 - t，没错我们就要整活。
因为4到t有限制，所以我们取的流为4。
接下来求出余图：

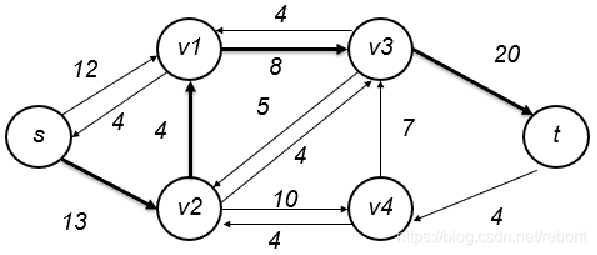
然后我们选择s - 2 - 1 - 3 - t的路径，最大因为2到3的限制，为4。

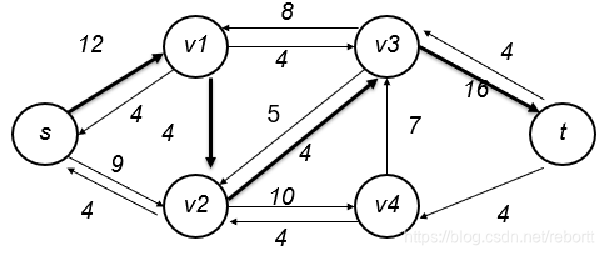
不断进行下取，最终的答案是这样的：

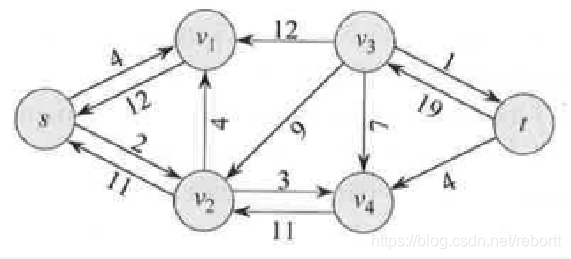
最大流加起来就是23

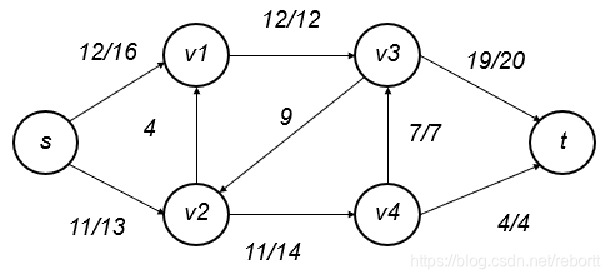
其实也不想要每一次记录流是多少，直接数最后的图都行，但是我们最好是看这张图，更明显：