Spatio-Temporal Channel Correlation Networks for Action Classification

最新推荐文章于 2024-05-18 12:43:38 发布

原创

最新推荐文章于 2024-05-18 12:43:38 发布 · 609 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #神经网络

本文提出了一种名为STC的时空通道相关网络，用于3D卷积神经网络中捕获时间、空间特征的关联信息。通过在2D CNN上预训练然后迁移至3D CNN，实现权重初始化，提高了在Kinetics数据集上的性能。STC网络包含SCB（空间通道块）和TCB（时间通道块），用于捕获通道间的时空相关性，有效地解决了3D CNNs的性能限制。实验表明，STC在视频分类任务中表现出色，尤其是在RGB数据上超越了其他方法。

Spatio-Temporal Channel Correlation Networks for Action Classification

Abstract

引入STC块对3D卷积神经网络进行关于时间、空间特征的建模。STC块嵌入目前先进的结构中能在Kinetic数据集上提高2-3%的性能。

在2D卷积神经网络上进行预训练，再将只是迁移到随机初始化的3D卷积网络中，实现稳定的权重初始化。（在Sports-1M上训练，在目标数据集HMDB51/UCF101上进行微调，便能超过其他的方法。）

Introduction

三维卷积神经网络的问题：

三维卷积神经网络忽略了通道之间的时空相关性的隐藏信息，这限制了这些体系结构的性能。
三维卷积神经网络需要超大的标记数据集。

以上的两个问题都会对计算效率和准确率造成负面影响。为避免这些限制，论文提出了：

STC模块——高效捕获时间通道和空间通道关联信息。
一个有效的监督转移——连接不同架构之间的知识转移，这样就不再需要从头开始训练网络。

STC

STC的功能是同时考虑时空特征上的通道间相关性信息，可以分为两个分支（设定输入为 $X∈RH×W×T×CX\in{\mathbb R}^{H\times W\times T\times C}$ ）：

SCB，考虑空间通道信息。空间全局池化产生的全局接受野的表达扮演两个重要角色：a) 考虑全局相关性通过聚合全局特征输入。b) 提供一个通道描述符分析通道之间的相关性。通道及的特征向量喂到两个bottleneck形状的全连接层来学习通道间的依赖关系。
TCB，考虑时间通道信息。有与SCB类似的过程，但用时间全局池化代替SCB的空间全局池化。

然后将以上两个分支的输出特征联合并作为STC块的输出。

有监督迁移

在ImageNet上训练2D卷积神经网络，将训练好的2D CNN进行有监督迁移，迁移到随机初始化的3D CNN来进行稳定的权重初始化。

这样可以避免巨额的计算工作量和训练时间。

网络结构如下：

在这里插入图片描述

Related Work

Video Classification with and without CNNs

未使用CNNs：HOG3D, SIFT3D, HOF, ESURF, MBH, iDTs, etc. 都是手动调整的。其中iDTs是最优秀的，待久就是计算成本昂贵并且缺乏补货语义概念的可拓展性。
使用了CNNs：分为2D——帧级和3D——视频级信息提取两种方式。2D使用LSTMs和RNNs来对独立帧进行建模以捕获长期时间依赖。通过特征聚合和编码来使用双线性模型、VLAD、Fisher编码等。还有一些3D卷积模型、光流卷积模型等等。

Transfer Learning

即在其他数据集上预训练好的网络放到目标数据集上进行微调。起到降低训练耗时的作用，即站在巨人的肩膀上。论文的Proposed Method中的transfer learning小节对文中使用的迁移学习方法进行了详尽的阐述。

Proposed Method

STC用于通过深度CNNs从视频中捕获不同的和新的信息。STC相关性模块在3D CNNs中提取不同层、不同通道中提取出不同通道的相关信息。此外，论文的另一个主要贡献，展示了跨架构(即2D→3D神经网络)之间的知识转移，从而避免了从头开始训练3Dcnn的需要。

STC Block

分为如下图中的TCB和SCB两条支路。每一条路径都有不同的模块；通道或卷积核信息嵌入和捕获依赖关系。论文提出的方法受到SENet论文中的方法的启发，即Squeeze-and-Excitation方法中所使用的全局平均池（空间和时间），和随后的两个bottleneck FC层和sigmoid激活函数。与SENet相比，STC块有两个分支，换句话说是双路径；一个考虑纯通道信息，另一个考虑时间通道信息。

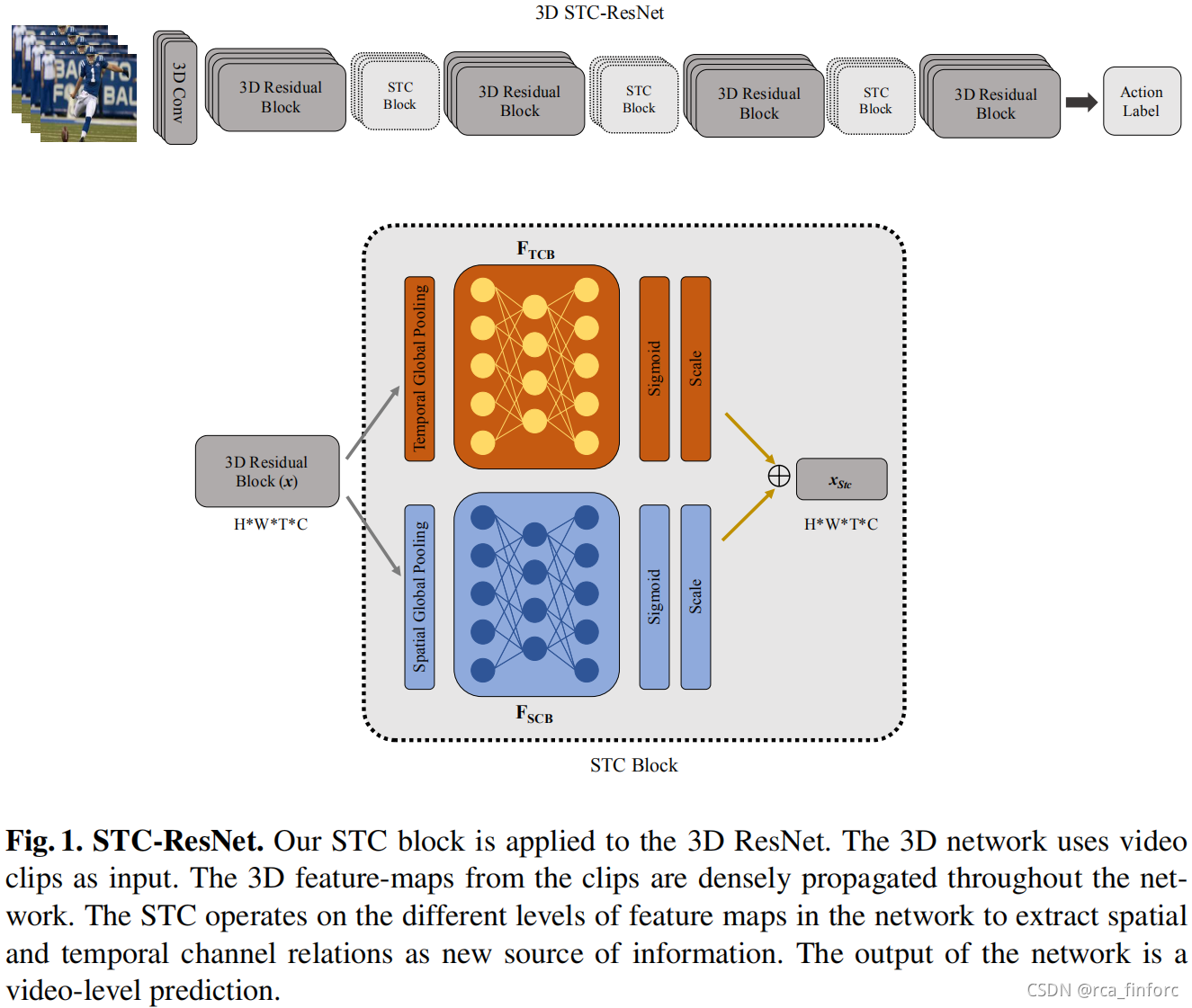
请添加图片描述

第 $l^{th}$ 层提取的输出特征图是一个张量 $X∈RH×W×T×CX\in{\mathbb R} ^{H\times W\times T\times C}$ ，这四个交表分别代表特征图的高、宽、时间深度和通道序号。3D卷积和池化核的尺寸是 $s×s×ds\times s\times d$ ， $d$ 代表时间深度 $s$ 代表卷积核的空间尺寸。

TCB

可以用以下公式来表达：
$\begin{aligned} z_{tcb}&=\frac{1}{W\times H\times T}\sum\limits_i^W\sum\limits_j^H\sum\limits_t^T x_{ijt}\\ s_{tcb}&=F_{tcb}(z_{tcb, W}) = W_2(W_1z_{tcb})\\ x_{tcb}&=s_{tcb}\cdot X \end{aligned}$