c++ 沙子合并（区间dp）以及优化

区间dp

定义

区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。

例题（沙子合并）：

设有N堆沙子排成一排，其编号为1，2，3，…，N（N<=300）。每堆沙子有一定的数量，可以用一个整数来描述，现在要将这N堆沙子合并成为一堆，每次只能合并相邻的两堆，合并的代价为这两堆沙子的数量之和，合并后与这两堆沙子相邻的沙子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同，如有4堆沙子分别为 1 3 5 2 我们可以先合并1、2堆，代价为4，得到4 5 2 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24，如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22；问题是：找出一种合理的方法，使总的代价最小。输出最小代价。

Input

第一行一个数N表示沙子的堆数N。

第二行N个数，表示每堆沙子的质量。 <=1000

output

合并的最小代价

---

考虑最后一次合并：

1…k合并为1堆p,k+1…n合并成一堆q

最后一次合并的代价是多少?

$$1+2+3+4+...+n$$

这不就是前缀和吗？

2.最优子问题：p,q的合并不受影响，可以对p和q再进行拆分

最后拆分长度为3、长度为2、长度为1的区间合并

3.状态：设$f_{i,j}$表示合并第$i$堆到第$j$堆的最小代价

4.转移方程：

fi,j=min{fi,j,fi,k+fk+1,j+sumj−sum−i−1}f_{i,j}=min\{f_{i,j},f_{i,k}+f_{k+1,j}+sum_j-sum-{i-1}\}fi,j​=min{fi,j​,fi,k​+fk+1,j​+sumj​−sum−i−1}

---

本题代码：

#include<bits/stdc++.h>
using namespace std;
int n,a[305],f[305][305],sum[305];//f(i,j)表示从第i堆沙子到第j堆沙子合并的最大值 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		sum[i]=sum[i-1]+a[i];//Input
	}
	for(int len=1;len<n;len++){//枚举其中一个区间的长度 
		for(int i=1;i+len<=n;i++){
			int j=i+len;
			//枚举决策点
			f[i][j]=0x7fffffff;//注意 
			for(int k=i;k<=j;k++){
				f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
			} 
		}
	}
	cout<<f[1][n]<<endl;
	return 0;
}

附录：区间dp的模板代码

#include <iostream>
#include <cstring>

using namespace std;

const int MAXN = 1005;   // 最大输入范围
int dp[MAXN][MAXN];      // dp数组

int main() {
    int n;              // 区间长度
    int a[MAXN];        // 区间元素
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    // 初始化dp数组
    memset(dp, 0, sizeof(dp));

    // 状态转移方程
    for (int len = 2; len <= n; len++) {
        for (int i = 1; i + len - 1 <= n; i++) {
            int j = i + len - 1;
            for (int k = i + 1; k < j; k++) {
                dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + a[i] * a[k] * a[j]);
            }
        }
    }

    cout << dp[1][n] << endl;   // 输出最终结果

    return 0;
}

时间复杂度：$O(n^3)$

好了，既然题目已经讲完了，我们的讲解~

没有结束！

区间dp的小优化（大大滴提高了时间复杂度）

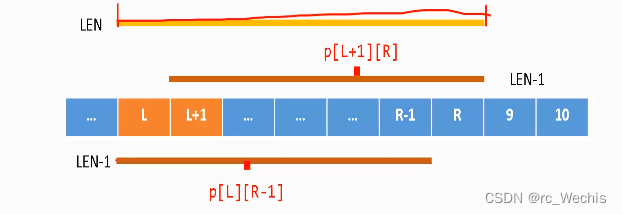
附上本题优化源码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,a[305],f[305][305],sum[305],q[305][305];//f(i,j)表示从第i堆沙子到第j堆沙子合并的最大值 
signed main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		sum[i]=sum[i-1]+a[i];//Input
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			f[i][j]=2147483647;
		}
		q[i][i]=i;
		f[i][i]=0;
	}
	for(int len=1;len<n;len++){//枚举其中一个区间的长度 
		for(int i=1;i+len<=n;i++){
			int j=i+len;
			//枚举决策点
			for(int k=q[i][j-1];k<=q[i+1][j];k++){
				if(f[i][j]>f[i][k]+f[k+1][j]+sum[j]-sum[i-1]){
					f[i][j]=f[i][k]+f[k+1][j]+sum[j]-sum[i-1];
					q[i][j]=k;
				}
			} 
		}
	}
	cout<<f[1][n]<<endl;
	return 0;
}

那我们今天的讲解就到这里