算法分析与设计——2.8 半数集问题

最新推荐文章于 2025-10-25 09:42:55 发布

原创最新推荐文章于 2025-10-25 09:42:55 发布 · 1w 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

算法分析与设计专栏收录该内容

15 篇文章

订阅专栏

本文探讨了半数集问题，给出了问题描述、算法设计和C++实现。通过对自然数n按照特定规则产生半数集，计算集合元素个数。递归算法的时间复杂度为O(n^n)，存在重复计算。文章提供了优化后的代码，减少了计算时间。

问题描述：给定一个自然数n，由自然数n开始可以依次产生半数集set(n)中的数如下：
                 (1)n属于set(n)
                 (2)在n的左边添加一个自然数，但该数不能超过最近添加的数的一半
                 (3)按此规则，直到不能添加为止
                 例如：set(6)={6,16,26,36,126,136}=6

算法设计：对于给定的自然数n，计算set(n)中的元素个数

输入：自然数n

输出：元素个数和元素内容

算法思想：以6为例。按照规则，新加入的数字小于等于6的一半——3。所以6进行一轮，添加了1，2，3三个数字组合为16，26，36。接下来发现只有26和36可以按照规则继续加数字。

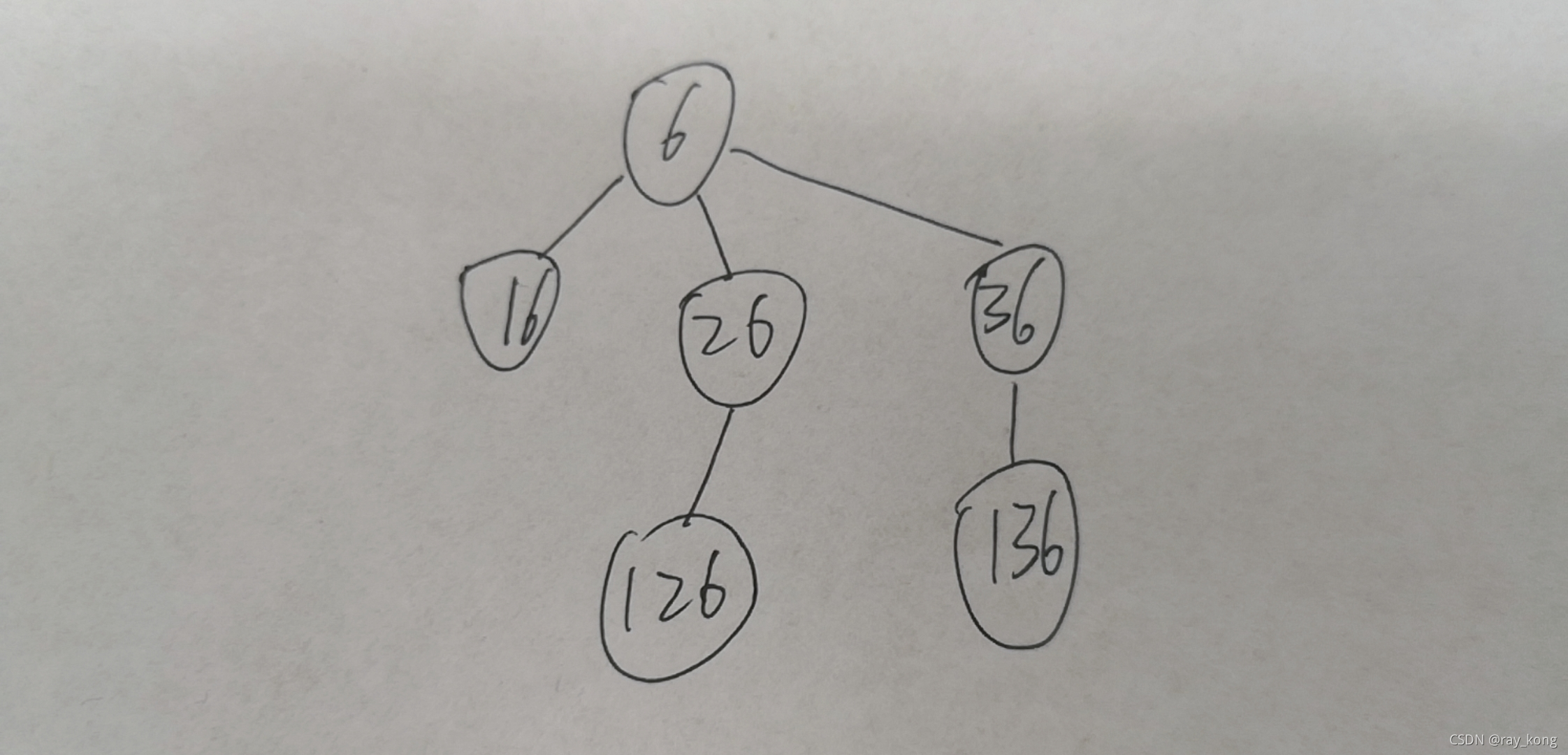
根据规则，对每一个数n最多可以添加n/2个数字且不重复，如果把每一个自然数看作树的节点，那么对一棵树上的节点来说都有n/2个子节点。符合分治策略的使用条件。有如下递归式：

根据树的性质，我们可以采用一维数组来遍历set(n)中的元素。

6
6	1
6	2	1
6	3	1

代码如下

#include<iostream>
#include<cstring>
using namespace std;
int a[10^5];

int  set(int n, int i) {
	a[i] = n;
	for (int j = i; j >= 1; j--) {  
		cout << a[j];
	}
	cout << endl;
	int ans = 1;
	for (int k = 1; k <= n / 2; k++) {
		ans += set(k, i + 1);
	}
	return ans;
}

递归的时间复杂度为O(n^n)。

通过递归式，我们发现包含许多重复计算和重复元素。重复计算浪费了很多计算时间。

对此，针对重复计算问题，优化代码如下：

//递归优化
int set_new(int n, int i)
{
	a[i] = n;
	for (int j = i; j >= 1; j--) {  //遍历数组(从后往前)
		cout << a[j];
	}
	cout << endl;
	int ans = 1;
	if (b[n] > 0)return b[n];
	for (int k = 1; k <= n / 2; k++) {
		ans += set(k, i + 1);
	}
	b[n] = ans;
	return ans;
}

对于半数单集问题：

//半数单集
int set_new_new(int n, int i)
{
	a[i] = n;
	for (int j = i; j >= 1; j--) {  //遍历数组(从后往前)
		cout << a[j];
	}
	cout << endl;
	int ans = 1;
	if (b[n] > 0)return b[n];
	for (int k = 1; k <= n / 2; k++) {
		ans += set(k, i + 1);
		if ((i > 10) && (2 * (i / 10) <= i))
			ans -= a[i / 10];
	}
	b[n] = ans;
	return ans;
}