基于皮带差动的肢体康复系统

肢体康复差动系统

1 引言

当出现神经或骨科损伤时，一些患者会表现出疼痛和/或一侧或双侧下肢功能的减退。因此，针对患者采用不同的康复方法，并研发了多种机器人装置以辅助康复过程。不同的测试表明，这些装置能够有效改善患者的功能表现 [1]。

目前市场上主要有两类设备：
– 下肢康复设备 – 旨在对肢体进行整体康复，具有或多或少复杂的结构，用于一次移动单个肢体，在这种情况下，患者坐着或躺着，医生将需要康复治疗的肢体与设备 [2–4] 连接；
– 步行再教育设备 – 相比前者具有更复杂的结构，由两个主要部件组成：悬臂系统，用于使患者保持直立姿势；以及肢体运动系统，通过适当的调节实现步态模拟 [5–7]。

这两种康复设备在设计上差异明显且相距甚远，因为它们被设计用于执行特定的康复任务。

本文旨在介绍一种用于下肢康复和行走再教育的新型模块化柔性装置（LEPRE）。该系统可用于下肢康复，也可通过连接特定附件实现上肢康复。此外，康复治疗可根据执行器是否启用，以主动模式或被动模式进行。

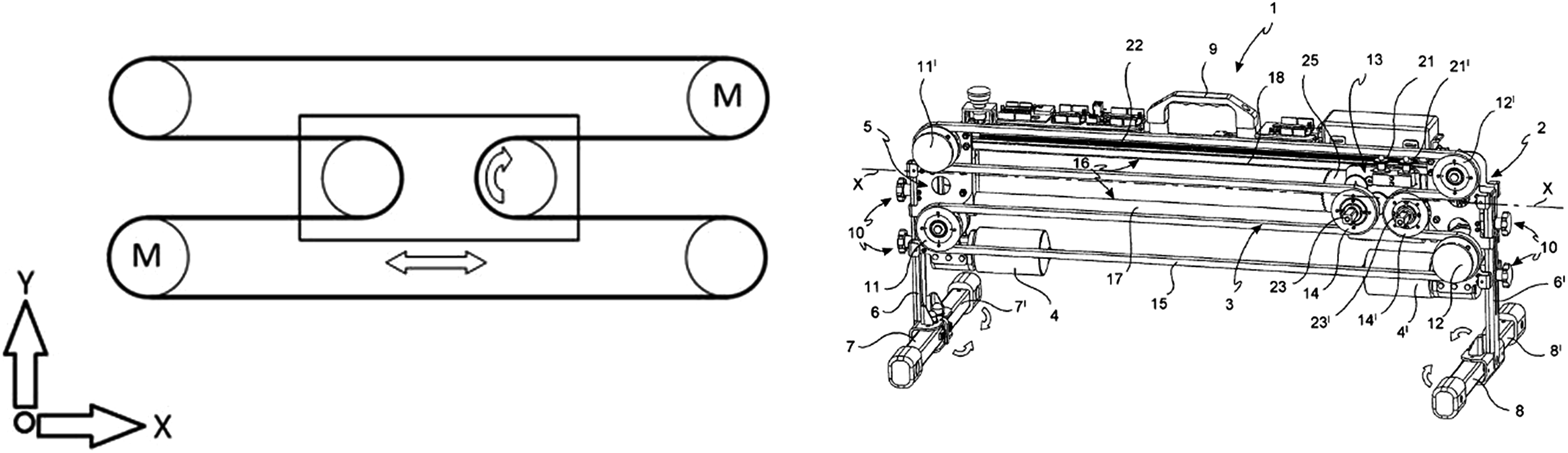
设备的部件被使用。该系统基于皮带式笛卡尔定位系统；在该系统中，两个适当安装并连接特定皮带和滑轮的电动机，可驱动放置在滑动导轨上的小车运动。待康复肢体的末端通过魔术贴条或杆连接至小车或滑轮。

2 问题定义

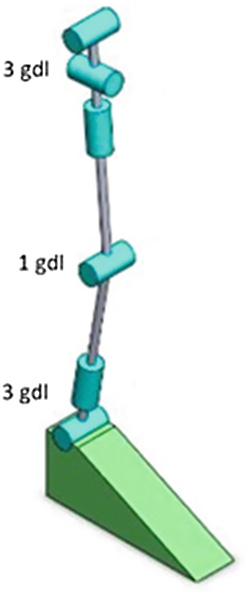
负责人体行走的下肢（图1）承担整个身体的重量，保证直立站立，并将重量传递至地面。

主要关节包括：
– 髋关节，连接骨盆与股骨
– 膝关节，连接大腿与小腿
– 踝关节，连接小腿与足部

步态是一种复杂的运动，因为在直立姿势下，下肢承受着全部的体重，而支撑面积——足部——非常小 [8, 9]。

这些条件迫使运动系统在控制过程中调动身体的所有部分，以实现期望的运动而不失去平衡状态。

行走过程中，身体持续围绕平衡位置移动，尽管这些位置并非稳定状态；各肢体之间相互传递的力和力矩通过关节、韧带和肌肉传递至躯干。

此外，还必须考虑惯性力的影响；这些力可能由上肢和脊柱关节产生，并与下肢动作相结合，从而产生所需的步态。

在步态过程中，运动器官执行的主要任务是：
– 产生推进力；
– 在姿势状态持续变化的情况下，仍保持较高水平的稳定性控制；
– 每一步吸收与地面撞击产生的冲击；
– 在前期阶段进行能量保存，减少肌肉用力。

当身体前进时，一个肢体支撑，另一个肢体向前移动直至下一次支撑；随后，两个肢体交换作用，在将身体重量从一个肢体转移到另一个肢体时，双脚均与地面接触。

这些任务的一个完整序列称为步态周期。

鉴于其复杂性，步态可分为两个主要阶段：支撑相，即足部与地面接触时；摆动相，即足部抬起，使肢体向前移动时。

此外，支撑相也可以分为三个子阶段：
– 初始双支撑相：在步周期开始时，对侧足初始触地后，双足均与地面接触的阶段；
– 单支撑相：从对侧足进入摆动相开始；
– 结束双支撑相：从对侧足初始触地开始，到最初处于支撑相的肢体离开地面进入摆动相时结束。

与地面接触相的典型分布大约为支撑相占60%，摆动相占40%。
支撑相的时相划分中，双支撑相各占10%，单支撑相占40%[10]。

3 解决方案与运动学模型

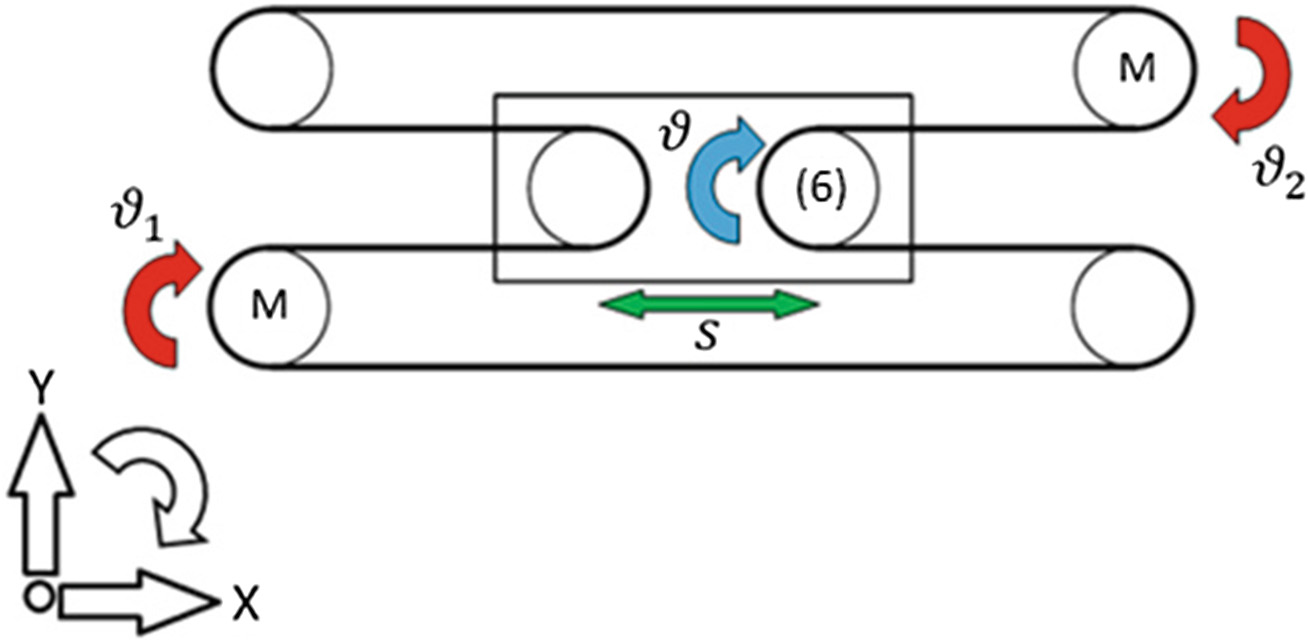
该系统基于连续皮带差动机构。如图2所示，X轴方向的运动由执行器及其指定的运动轮廓保证，而Y方向的运动则通过与同一拖车上的某个滑轮正确连接的附件实现。这样，即可在整个XY平面内进行运动。

该系统具有单轴运动结构和两个自由度：小车的平移以及皮带与滑轮之间的相对运动（图3）。

– 小车的运动

参考图3，当滑轮2保持固定而滑轮1可自由移动时，小车位移可用关系式（1）表示。
同样地，无论滑轮1是固定的还是滑轮2旋转，由关系式(2)描述的线性位移均可获得。

$$
s_1 = \frac{\theta_1 r_1}{2} \quad (1)
$$

$$
s_2 = \frac{\theta_2 r_2}{2} \quad (2)
$$

当滑轮1和滑轮2同时旋转时，小车的总位移等于前述方程之和，如关系式（3）所述。

$$
s = s_1 + s_2 = \frac{\theta_1 r_1 - \theta_2 r_2}{2} \quad (3)
$$

通过对关系（3）对时间求导，可以计算出小车速度，如公式（4）所示。
最后，通过对关系（4）关于时间求导，也可以得到小车加速度，如公式（5）所示。

$$
v = \frac{\dot{\theta}_1 r_1 - \dot{\theta}_2 r_2}{2} \quad (4)
$$

$$
a = \frac{\ddot{\theta}_1 r_1 - \ddot{\theta}_2 r_2}{2} \quad (5)
$$

– 滑轮旋转

滑轮6的旋转由关系式(6)给出。

$$
\theta = \frac{\theta_1 + \theta_2}{2} \quad (6)
$$

因此，速度和加速度可以根据关系式（7）和（8）进行评估。

$$
\omega = \frac{\dot{\theta}_1 + \dot{\theta}_2}{2} \quad (7)
$$

$$
\alpha = \frac{\ddot{\theta}_1 + \ddot{\theta}_2}{2} \quad (8)
$$

下文将针对以下假设，对所提出的差动系统进行动态分析：（i）直接施加于小车的水平力；（ii）通过附件施加于小车的力，其中用户脚部放置在该附件上。

4 动态分析

– 在假设对小车施加水平力的情况下的动态分析

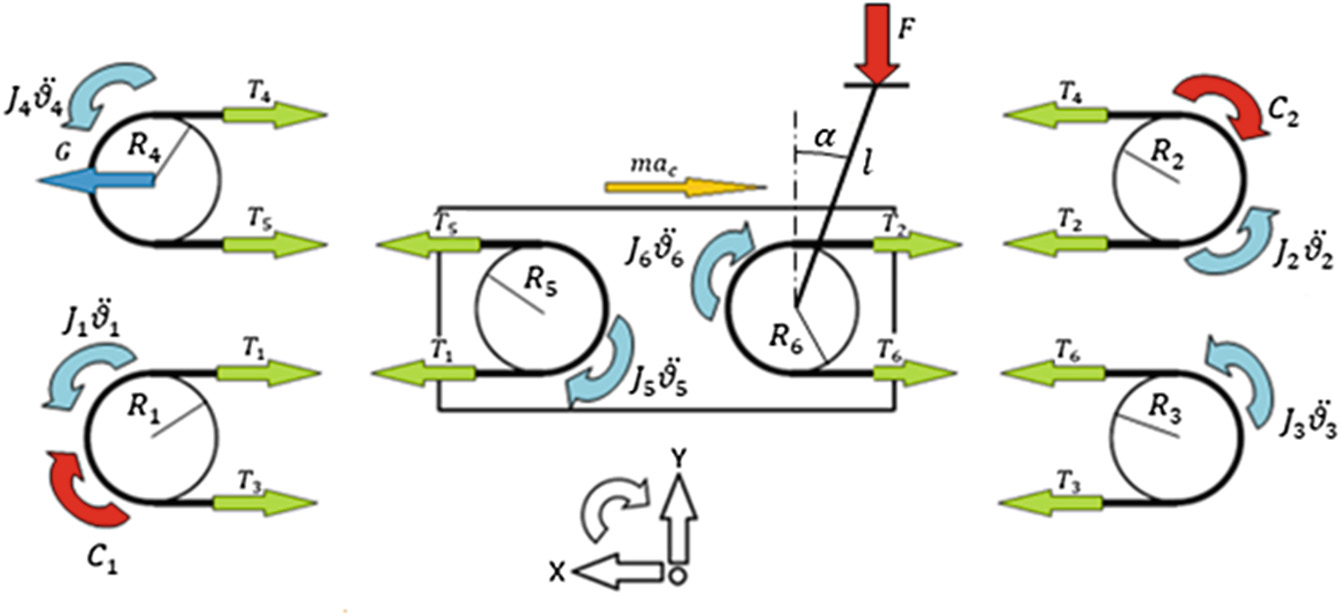
为了研究系统的动力学特性，进而估算皮带张力和执行器扭矩，对该机构进行了划分，以便突出作用在皮带不同段上的力。

这样就产生了八个未知量，如图4所示：其中六个由各段皮带张力产生，另外两个由反向扭矩给出。

因此，从机构各部件的平衡方程到旋转和平移，可选择八个关系（9–16）来构建一个八变量求解系统。

$$
T_4 R_4 - T_5 R_4 - J_4 \ddot{\theta}_4 = 0 \quad (9)
$$

$$
C_2 - J_2 \ddot{\theta}_2 - T_4 R_2 + T_2 R_2 = 0 \quad (10)
$$

$$
T_2 R_6 - T_6 R_6 + J_6 \ddot{\theta}_6 = 0 \quad (11)
$$

$$
T_3 R_3 - T_6 R_3 - J_3 \ddot{\theta}_3 = 0 \quad (12)
$$

$$
C_1 - J_1 \ddot{\theta}_1 - T_3 R_1 + T_1 R_1 = 0 \quad (13)
$$

$$
T_1 R_5 - T_5 R_5 + J_5 \ddot{\theta}_5 = 0 \quad (14)
$$

$$
G - T_4 - T_5 = 0 \quad (15)
$$

$$
F + T_5 + T_1 - T_2 - T_6 - m a_t = 0 \quad (16)
$$

– 在假设力作用于约束在小车滑轮上的曲柄时的动态分析：

在这种情况下，新的力配置允许选择公式(17–24)来构建求解系统。

$$
T_4 R_4 - T_5 R_4 - J_4 \ddot{\theta}_4 = 0 \quad (17)
$$

$$
C_2 - J_2 \ddot{\theta}_2 - T_4 R_2 + T_2 R_2 = 0 \quad (18)
$$

$$
T_2 R_6 - T_6 R_6 + J_6 \ddot{\theta}_6 + F l \sin \alpha = 0 \quad (19)
$$

$$
T_3 R_3 - T_6 R_3 - J_3 \ddot{\theta}_3 = 0 \quad (20)
$$

$$
C_1 - J_1 \ddot{\theta}_1 - T_3 R_1 + T_1 R_1 = 0 \quad (21)
$$

$$
T_1 R_5 - T_5 R_5 + J_5 \ddot{\theta}_5 = 0 \quad (22)
$$

$$
G - T_4 - T_5 = 0 \quad (23)
$$

$$
T_5 + T_1 - T_2 - T_6 - m a_t = 0 \quad (24)
$$

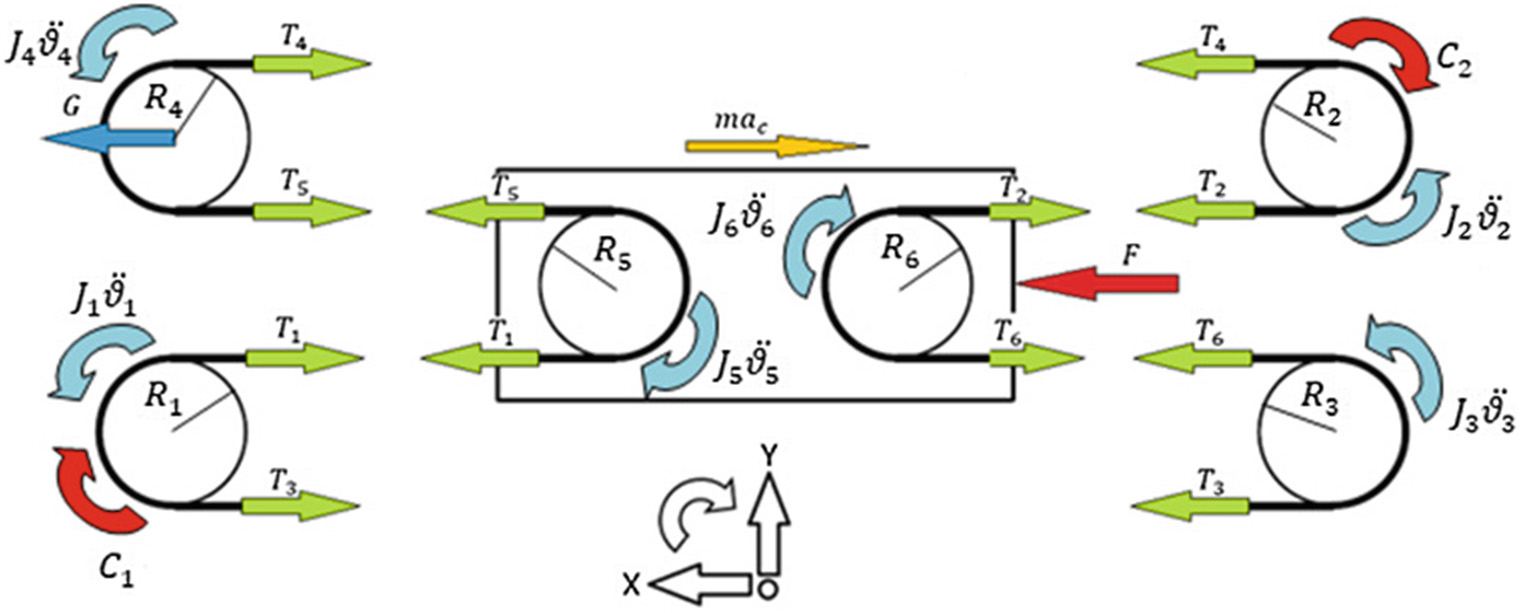
图6显示了正常人类受试者踝关节的理想运动与所提出的装置实现的运动的一个示例，其中仅可观察到一些可接受的差异。受试者的足部连接到图5中所示杆 $ l $ 的上侧。

5 结论

康复如今涉及许多专业领域：除了医学领域，还有物理、数学和工程等领域。

正是出于这一原因，一种用于步态再教育的新概念装置被设计出来，这种装置新颖且针对这一复杂任务进行了优化。这得益于采用了基于皮带的差动系统，该系统在使用和调节策略上提供了灵活性。这种多功能性主要源于能够通过作用于连接到执行器的滑轮的旋转、滑轮的尺寸或控制电子设备来实现不同类型的运动。

根据本简要论述中所述内容，可以最终确定，基于皮带的差动系统，更具体地说LEPRE，因其相对简单和多功能性，可被视为康复应用的一种有效解决方案。