高维数组的切片、索引操作汇总（附axis解析）

癞皮狗狗主

已于 2023-02-12 19:57:36 修改

阅读量401

点赞数 2

文章标签： python numpy

于 2023-01-08 00:29:47 首次发布

本文链接：https://blog.youkuaiyun.com/raozhizhenshuai/article/details/128590881

版权

本文通过实例详细解释了numpy数组的切片和索引操作，使用图形辅助理解，包括三维数组的切片以及不同维度上的sum操作。读者可以跟随示例掌握如何根据轴(axis)进行操作并理解其对数组形状的影响。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

高维数组的切片、索引操作是基础中的基础，一定得理解。现在很多文章没有用图示的形式加深理解，本文力求结合图形帮助理解

import numpy as np
demo = np.arange(24).reshape(3, 2, 4)

# demo的输出：
[[[ 0  1  2  3]
  [ 4  5  6  7]]

 [[ 8  9 10 11]
  [12 13 14 15]]

 [[16 17 18 19]
  [20 21 22 23]]]

a = demo[:, :, :2]

print(a)
print(a.shape)

输出：
[[[ 0  1]
  [ 4  5]]

 [[ 8  9]
  [12 13]]

 [[16 17]
  [20 21]]]

(3, 2, 2)

切片看状态 (切片前后的状态)
Dim 0不动（还是3),
Dim 1不动 (还是2),
Dim 2保留了前两个(变成了 2)
最后的shape应该是 (3, 2, 2), 完全没问题。最后a的示意图如下：

a = demo[:2, :, 2]
print(a)
print(a.shape)

# 输出
[[ 2  6]
 [10 14]]
 
 (2, 2)

Dim 0保留前两个（变成了2),
Dim 1不动 (还是2)
Dim 2保留了之前的第3个(变成了 1，索引是2对应第三个)
最后的shape应该是 (2, 2), 1就不显示出来，完全没问题

可以按照这样的思路，根据例子输出结果以此类推你需要的形式…

通过笔者实验发现Dim 与 axis 是对应的，下面用np.sum()举例子

先创建一个shape = (2, 2, 4) 的 ndarray

img = np.array([
    [[0,1,2,3],
     [0,0,1,0]],
    
    [[1,1,0,3],
     [0,1,1,0]]
])

print(img)
print(img.shape)

# 输出
[[[0 1 2 3]
  [0 0 1 0]]

 [[1 1 0 3]
  [0 1 1 0]]]
  
(2, 2, 4)

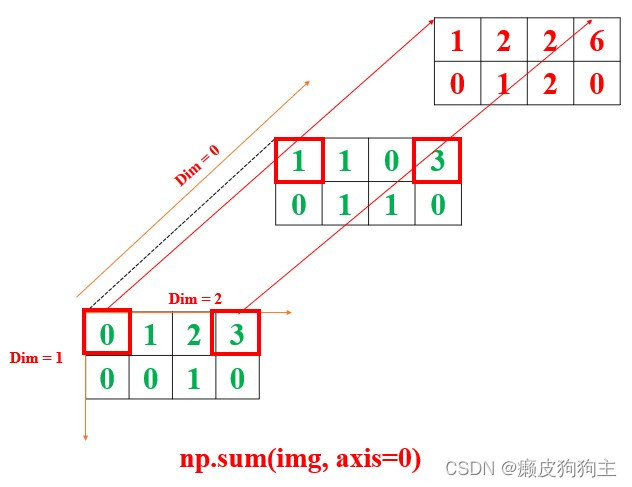
axis=0, 在“1”的维度上进行sum操作

np.sum(img, axis=0)

# array([[1, 2, 2, 6],
#        [0, 1, 2, 0]])

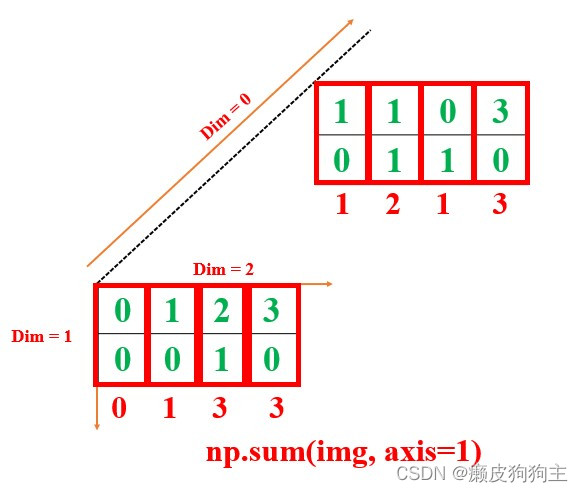
axis=1, 在“1” 的维度上进行sum操作

np.sum(img, axis=1)

# array([[0, 1, 3, 3],
#        [1, 2, 1, 3]])

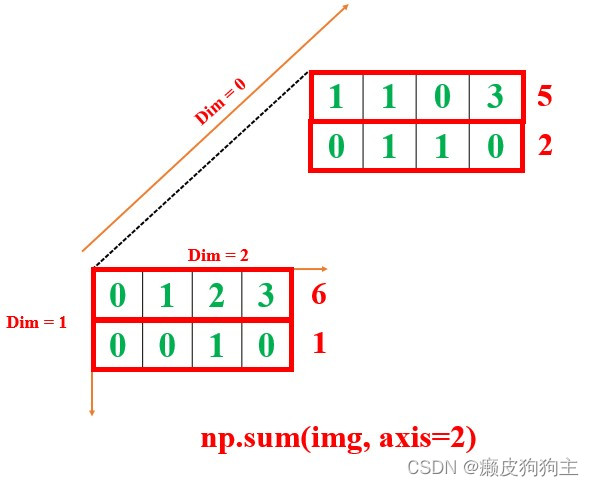
axis=2，在“2” 的维度上进行sum操作

np.sum(img, axis=2)

# array([[6, 1],
#        [5, 2]])