边缘计算优化用于高效 RRH‐BBU(射频拉远单元‐基带处理单元)分配在云无线 接入网络
Niezi Mharsi a , b , ∗, Makhlouf Hadji b a巴黎理工学院,电信巴黎高科,巴罗街46号,巴黎75013,法国b系统X研究所,沃夫大道 8号,帕莱索91120,法国
摘要
云无线接入网络(C‐RAN)作为一种有前景的架构被提出,以应对下一代移动网络(5G)面临的挑战。C‐RAN 的核心思想是将基带处理单元(BBU)与远程射频单元(RRH)分离,并将BBU集中放置于公共的边缘数据中心 (或BBU池)中进行集中化处理。在联合优化前传延迟和资源消耗的前提下,如何将RRHs(或天线)最优分配 至边缘数据中心,是C‐RAN部署中的关键问题之一。该问题属于NP‐难问题,网络运营商需要能够适应大规模问 题规模并在可接受时间内找到良好解的新分配算法。本文中,我们首先基于整数线性规划(ILP)建立精确方法对 约束资源分配问题进行建模。然后,为了提高可扩展性,我们提出了具有较低复杂性的新启发式算法,以快速获 得天线需求到可用边缘数据中心分配问题的最优或近似最优解。仿真结果突出了所提出的近似算法在效率和可扩 展性方面的优势,并表明其能够在可忽略的时间内提供高质量的解。
© 2019 Elsevier B.V.保留所有权利。
1. 引言与动机
为了应对电信领域中动态且不断增长的终端用户需求,电信服务提 供商(TSPs)正在探索新的解决方案,以降低其新型基础设施的资本支 出(CAPEX)和运营支出(OPEX),这些基础设施通常基于网络功能 虚拟化(NFV)范式[1] 。事实上,通过共享其NFV基础设施(NFVI), 这些运营商可以显著降低运营成本,从而在满足更多终端用户和新虚拟 化服务订阅者需求的同时实现利润最大化。
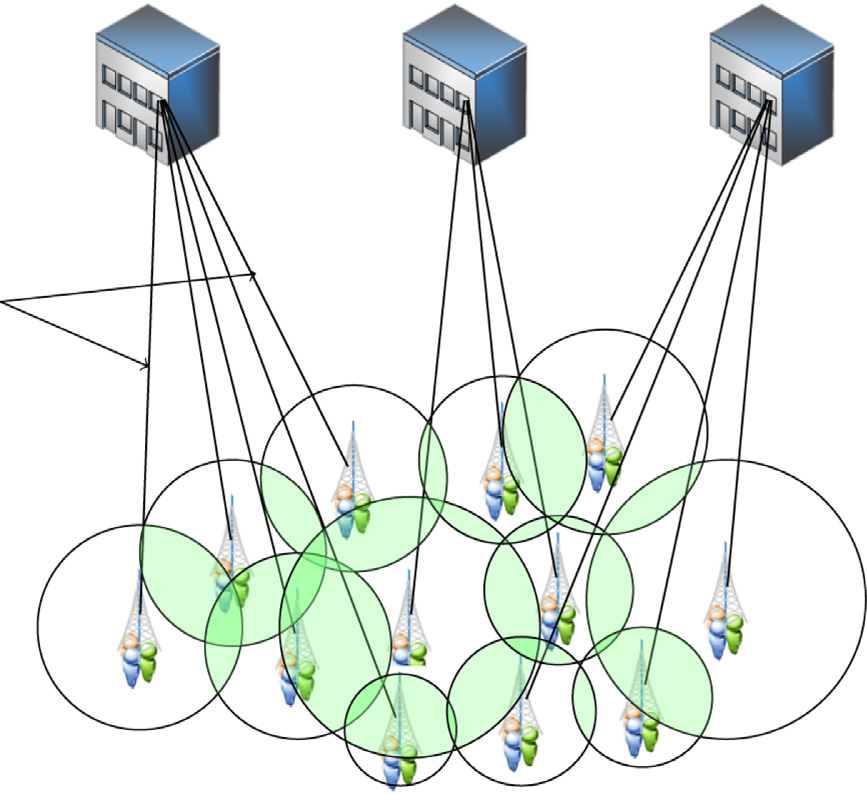
无线接入网络(RAN)的虚拟化和云化已被认为是有效优化这些参 与方网络部署成本(如资本支出和运营支出)的良好候选方案。在此背 景下,C‐RAN 被提出作为下一代移动网络的一种有前景的网络架构, 它结合了网络功能虚拟化(NFV)和云计算概念,以提高网络利用效率 并实现成本节约。事实上,与传统的将基带功能与天线共同部署在基站 站点上的网络不同,C‐RAN 将传统基站解耦为RRHs和集中式的BBU,后者被汇集在称为BBU池的 共用位置,并作为多个基站站点之间的共享资源。图1展示了C‐RAN架 构,并聚焦于三个主要组成部分:(i)RRHs(天线),(ii)BBU池 (边缘数据中心)和(iii)前传网络。
C‐RAN中计算资源的集中化能够实现成本节约和资源利用率提升 (例如参见[2–4], )。然而,只有在将具有严格延迟和处理要求的异构 天线需求最优地分配给可用边缘数据中心时,才能实现这些收益。因此, 电信服务提供商(TSPs)正在研究新的资源分配算法,以在同时满足延 迟和处理需求的前提下,高效地将边缘数据中心有限的处理资源分配给 天线需求。
1.1. 目标与贡献
本文重点在于提出新的优化算法,以高效地将天线需求分配给边缘 数据中心,从而在满足前传网络严格时延要求的同时,提高网络资源利 用效率。为实现这些目标,我们提出了一种基于整数线性规划(ILP) 公式的精确方法,以推导出合适的算法,用于求解RRH‐BBU分配问题 的最优解。

精确方法通过联合降低前传延迟和资源消耗,提供了最佳的RR H‐BBU(射频拉远单元‐基带处理单元)分配策略。然而,ILP方法仅能 处理小规模和中等规模的问题实例。因此,针对更大规模的问题实例, 我们提出了三种基于精确理论和方法的近似算法,这些算法具有良好的 可扩展性且收敛速度合理。我们提出的算法,包括精确算法和启发式算 法,总结如下:
- ILP公式 :这是一种基于约束资源分配问题凸包描述的精确方法, 用于确定将天线需求分配给可用边缘数据中心的最合适策略。所提 出的ILP公式将联合优化通信延迟和网络资源消耗。该方法可保证 RRH‐BBU分配问题的最优解。
- 基于拟阵的算法 :我们提出一种基于拟阵理论[5]的新型近似算 法来处理RRH‐BBU分配问题。拟阵是一种精确方法,我们对其稍作 修改,从而为所研究的问题提出一种启发式算法。值得注意的是, 这是首次在C‐RAN背景下使用拟阵理论来解决约束资源分配问题。
- 基于b‐匹配的算法 :我们研究了一种基于新的公式化方法, 该方法采用 b‐匹配方法[6] ,旨在满足预期通信延迟的同时,在 处理容量受限的情况下,寻找天线与边缘数据中心之间最小权重的 匹配。
- 基于多背包的算法 :我们提出了一种基于多背包公式化的近似算 法,该方法在文献中已被广泛用于解决多种资源分配问题的变体 (例如[7–10] )。在本文中,我们使用多背包公式化来解决 C‐RAN环境下的RRH‐BBU分配问题。
1.2. 论文结构
本文的其余部分组织如下:第2节致力于深入分析文献中与 RRH‐BBU分配问题最相关的工作。第3节描述了我们针对该问题的系统 模型并进行了讨论其复杂性。第4节介绍了我们提出的算法,包括精确算法和启发式算法。第5节通过多个场景的数值结果展示了所提出算法的性能。第6节给出了 结论和未来研究挑战。
2. 相关工作
C‐RAN架构的部署将多个基站站点共享基础设施,有望降低网络成 本(资本支出和运营支出),并提高资源利用效率[11] 。为了实现这些 目标,电信服务提供商(TSPs)正在研究新算法,以确定在共同满足严 格的延迟要求和天线需求的处理需求时,将RRHs分配给BBUs的最佳策 略(即RRH‐BBU分配问题)。
在此背景下,米君比等人[12]和余等人[13]讨论了应对 RRH‐BBU分配问题的新型数学建模方法。他们提出了一种基于ILP方法 的数学公式化,其中仅考虑了BBU处理能力约束。所提出的精确优化模 型未考虑前传网络上的传输延迟以及天线需求的时延要求。为应对可扩 展性问题,这两项研究均提出了近似算法,但不能保证收敛到最优解。
在本文中,我们研究了在满足严格的延迟要求并尊重边缘数据中心的容 量限制约束条件下的RRH‐BBU分配问题。我们的联合优化首先通过精 确公式化表示,随后研究能够在可接受时间内收敛到近优解的启发式算 法。
米什拉等人 [14]提出了一种RRHs与BBUs之间的负载感知动态映 射,旨在最小化处理计算资源需求所需的激活BBU数量。作者引入了一 种启发式DRA(动态RRH分配)以动态优化BBU池化增益。他们声称, 与首次递减适应(FFD)算法相比,该方法在计算资源增益和收敛时间 方面几乎达到了最优性能。类似地,另一项研究在[15]中提出了一种资 源分配算法,以最小化为服务网络中所有用户所需的激活BBU数量,从 而节约更多能源。在我们的工作中,除了使用提出的ILP公式作为其他 算法的基准外,还提出了三种启发式方法,以确保约束资源分配问题在 可忽略的时间内收敛至最优解。
另一项针对RRH‐BBU分配问题的研究在[16]中被提出。事实上, 该论文的作者提出了一种贪心算法,将每个小区的聚合需求分配给基带 处理单元池,以最小化物理资源的功耗。作者在其优化模型中未考虑小 区的时延要求。由于在C‐RAN环境中时延和传输延迟约束非常严格,我 们提出基于通信延迟与计算资源分配联合优化的精确与启发式算法。
在[17] , 霍尔姆等人提出了一种基于整数线性规划的数学公式化方 法,以最优地将天线需求分配到不同的BBU池。该研究旨在最小化光纤 长度,同时最大化承载基带功能的每个BBU池的统计复用增益。所提出 的方法表明,RRHs到BBU池的最优分配取决于光纤长度和BBU资源。本文中,我们为同一问题提出了一个精确公式化,并为进一步扩展,致 力于研究新的快速方法。
Boulos等人[18]研究了新的算法,以通过寻找现有RRHs的最优 聚类来确定RRH‐BBU映射的最佳策略。他们将此问题建模为装箱问题, 并考虑了两个主要约束条件:(i)每个激活BBU的无线资源必须足以满 足其映射RRHs的需求;(ii)分配给一个BBU的天线集合应地理上相邻。文中提出了精确与启发式算法,在保证终端用户良好服务质量(QoS) 的同时降低网络功耗。然而,所提出的模型未考虑连接RRHs与BBU池 的前传网络中的通信延迟。在本研究中,我们通过基于ILP模型的精确 方法和近似算法解决了同一问题,综合考虑BBU池的有限处理能力以及 前传链路的传输延迟,寻找天线到集中式数据中心的最佳分配方案。
Musumeci等人[19]提出了一种基于整数线性规划(ILP)公式的 精确方法,用于确定在波分复用(WDM)汇聚网络上BBU池的最优部 署。他们的优化方案在满足前传网络严格的延迟要求的同时,联合最小 化所需BBU池的数量和光纤链路的总数。在本文中,除了ILP公式外, 我们还提出了三种近似算法,以在考虑不同传输需求和BBU池处理能力 有限容量的情况下,为天线需求分配到集中式数据中心提供有效的策略。我们提出的算法旨在同时满足时延要求,并在所需BBU池数量方面实现 资源利用率提升。基于ILP方法得到的解将被用作性能基准在资源利用率、收敛时间以及可扩展性方面,我们的启发式算法的性能。
Santoyo‐Gonzlez 和 Cervell‐Pastor [20]讨论了在满足5G移动 网络需求的前提下,雾计算/NFV环境(相当于C‐RAN场景中的BBU池) 中雾节点的部署问题。他们提出了一种基于混合整数线性规划( MILP)的数学建模方法,旨在严格满足时延要求和有限处理能力约束 的同时,最小化雾节点的数量及其容量。为了提高可扩展性,他们进一 步提出了一种名为混合模拟退火(Hybrid‐SA)的启发式算法,该算法 结合了SA方法和一些局部搜索技术,以减少获取解所需的时间,尤其适 用于大规模问题实例。仿真结果突出了Hybrid‐SA算法的效率及其在最 小化雾节点数量方面的能力。然而,在考虑大规模问题实例时,该算法 的收敛时间仍然偏高。在本文中,我们研究了一种基于ILP模型的精确 方法以及三种具有相似目标和约束条件的启发式算法,用于解决 C‐RAN场景下的RRH‐BBU分配问题。根据不同的性能指标,我们深入 分析了所提启发式算法的性能,旨在即使面对大规模网络规模,也能在 可忽略的收敛时间(相较于Hybrid‐SA算法的收敛时间)内提供最优解 或近似最优解。
其他一些现有研究(例如 [21–23] )在 C‐RAN 环境下探讨了资源 分配问题,仅关注最小化 BBU 池中的能耗,而未考虑前传延迟约束。在本研究中,我们寻求新算法,通过联合优化资源消耗和通信延迟来降 低网络成本,以实现计算资源的最优利用。

3. 问题描述
在本节中,我们描述了用于解决RRH‐BBU分配问题的系统模型, 并介绍了问题描述中使用的所有变量和参数。接着,在提出我们的算法 之前,我们讨论了在考虑下文将定义的所有约束条件时,RRH‐BBU分 配问题的复杂性。
3.1. 系统模型
我们考虑如图2所示的系统模型,以定义约束资源分配问题,该问题 旨在当满足严格的延迟和处理要求时,将天线需求高效地分配给最合适 的边缘数据中心。我们的系统模型表示一个C‐RAN网络,其中RRHs (天线)和BBU池(边缘数据中心)部署在一个大区域中。如图2a所示, 我们的网络架构包含一组天线,记为I,每个天线由其在平面上的位置定 义。这些天线i ∈ I具有可变的预期延迟l_i和以CPU核心表示的处理需求 c_i,具体取决于聚合终端用户需求。RRHs由一组有限的可用边缘数据 中心提供服务,记为J。每个边缘数据中心j ∈ J具有有限的计算处理能力 C_j,以CPU核心数表示。
天线通过前传网络连接到边缘数据中心,该网络由一组通信链路表示。天线i ∈ I与边缘数据中心j ∈ J之间的每条前传链路都有传输延迟L_ij,为 满足混合自动重传请求(HARQ)1要求(参见[2,24,25] ),此延迟应 保持在1毫秒以下。这要求RRH i与BBU池j之间的最大距离d_ij不得超过 20‐40公里([2,26] )。前传网络上的数据流量可以使用不同的协议传输, 最常见的是CPRI [27], ,在某些情况下是OBSAI [28] 。在我们的系统模 型中,根据陈及其合作者[2,29],,前传网络上的传输延迟为5 μ秒/公里, 因此RRHs与BBU池之间的通信(前传)延迟最多在100到200 μ秒之间。
如图2所示,我们的网络拓扑(图2a)可以建模为一个加权二分图 G =(I ∪ J, E) ,其中一侧为天线集合I,另一侧为边缘数据中心集合J,前传链路由边集E表示。图G中每条边上的权重值记为L ij,表示天线i ∈ I与边缘数据中心j ∈ J之间的通信延迟。该二分图G =(I ∪ J, E)将用于在 满足处理和时延要求的前提下,高效地将每个天线精确分配给一个边缘 数据中心。
为了清晰起见,我们在图3中给出了一个由6个RRHs(天线)和2个边缘数 据中心(BBU池)和由一组通信链路表示的前传网络网络由通信链路集表示。约束资源分配问题在于确定在严格的处理和时延要求下,将天线需 求分配给可用边缘数据中心的最优策略。因此,我们的目标是在图3 a的 二分图中,选择所有考虑的天线与可用边缘数据中心之间的最优匹配。当延迟和资源消耗(使用的边缘数据中心数量)最小时,即实现了所有 考虑的天线到BBU池的最优分配。右侧图形(图3 b)表示RRH‐BBU分 配问题的一个可行解。
为了清晰起见 ,我们在此总结 表 1中列出所有变量和参数 和参数 ,这些 变量和参数将在后续内容中用于建模约束资源分配问题 。在接下来的部分中 ,将使用 这些变量和参数来建模 约束资源分配问题 。问题
| 变量和参数 | 描述 |
|---|---|
| G=(I ∪ J, E) | 加权二分图 |
| I | 天线/射频拉远单元集合 |
| J | 边缘数据中心/基带处理单元池集合 |
| E | I 和 J 之间的通信链路集合 |
| d_ij | 天线 i(坐标为 (xi, yi))与边缘数据中心 j(坐标为 (xj, yj))之间的距离 |
| c_i | 处理天线 i 的聚合需求所请求的CPU核心总数 |
| Cj | 每个边缘数据中心 j 中可用的计算资源(CPU核心) |
| l_i | 处理天线 i 的聚合需求的预期延迟 |
| L_ij | 天线 i 与边缘数据中心 j 之间通信链路上的传输延迟(延迟) |
3.2. 问题复杂性
在研究用于解决RRH‐BBU(射频拉远单元‐基带处理单元)分配问 题的新算法之前,本节首先讨论该问题的复杂性。我们提供了一个定理 及其证明,以确认该问题的NP难性。
定理 3.1。 将天线(RRHs)需求最优分配给可用边缘数据中心(BB U池)是一个NP-难问题。
证明。 如上所述,约束资源分配问题的目标是寻找天线需求到可用边缘 数据中心的最优分配方案,以满足延迟和处理需求,并最小化网络资源 利用率。我们的问题与广义分配问题(GAP)(参见[30]以了解详细信 息)密切相关,而GAP是多背包问题[31]和装箱问题[32]的经典泛化形 式。实际上,GAP的目标是在满足容器容量限制的前提下,将物品(每 个物品具有尺寸和利润)进行可行打包,以最大化总利润。
我们的约束资源分配问题与GAP非常相似,其中天线可以被视为物 品,边缘数据中心则是容器。此外,与GAP相比,我们的约束资源分配 问题还增加了关于连接天线和边缘数据中心的通信链路时延要求的约束 条件。因此,放宽这些约束条件后便得到一个GAP实例,这意味着 GAP的最优解是RRH‐BBU分配问题的一个可行解(不一定是最优解)。卡特里斯及其合作者 [31,33] 已证明了Gap的NP难。因此,通过我们的问题到 Gap的前述线性约简,我们可以推断出我们的RRH‐BBU分配问题也是NP‐难的,这意味着将天线需求最优分配给可用边缘数据中心是一个NP‐难问题。
4. 提出的算法
在本节中,我们提供了一种基于整数线性规划(ILP)公式的精确 方法,以确定天线需求到边缘数据中心的最优分配。由于所讨论问题的 NP难特性(参见第3.2节中的证明),我们提出了三种近似算法,以快 速处理大规模问题实例下的RRH‐BBU分配问题。
4.1. 基于整数线性规划模型的数学表述
在本节中,我们研究了一种基于ILP方法的新的数学建模,以最优 求解RRH‐BBU分配问题。值得注意的是,该方法旨在为中小规模网络 提供最优解,这些最优解将随后作为基准,用于根据多个性能指标评估 我们所提出的启发式算法的性能。
4.1.1. 决策变量
我们通过引入两个决策变量来开始对问题的建模,如下所示:
- x_ij是一个二进制决策变量,当<天线>i ∈ I被分配给边缘数据中 心j ∈ J时,其值为1,否则为0。
- y_j是一个二进制决策变量,其值为 1表示边缘数据中心 j被使 用(激活)以托管至少一个RRH (天线),否则为 0。
4.1.2. 目标函数
我们RRH‐BBU分配问题的目标是在共同满足天线需求的处理和时 延要求的前提下,将最合适的(“最佳”)边缘数据中心的计算资源高 效地分配给天线需求。该目标将通过在前传网络的传输需求与边缘数据 中心数量之间找到最佳权衡来实现。活跃的边缘数据中心。事实上,类似于[12,19,21,34],我们的目标函数 (1)包含两个项:第一项表示前传网络中通信延迟方面的总分配成本,第二项表示已使用边缘数据中心的网络资源利用率。通过使用该目标函数, 我们旨在为RRH‐BBU分配问题寻找一个最优解,这相当于在最终图中 对所有天线与可用边缘数据中心进行最优匹配,同时联合优化延迟和资 源消耗(如图2示例所示)。
$$
\min F= \sum_{j\in J} \sum_{i \in I} L_{ij} \times x_{ij}+ \sum_{j\in J} y_j \tag{1}
$$
4.1.3. 约束条件
约束条件(2)确保每个天线i恰好连接到一个边缘数据中心j。这些约 束条件在图3的图解方案中被考虑,其中每个天线恰好映射到一个边缘 数据中心。
$$
\sum_{j\in J} x_{ij}= 1, \quad \forall i \in I \tag{2}
$$
约束条件(3)确保将天线需求分配给BBU池时,不会违反边缘数据中 心的容量限制约束。实际上,如第3.1节所述,每个边缘数据中心j在 CPU核心方面具有有限的处理能力C_j,因此处理所有天线所需的CPU核 心总数不得超过所选边缘数据中心的可用计算资源。
$$
\sum_{i \in I} c_i \times x_{ij} \le C_j \times y_j , \quad \forall j \in J \tag{3}
$$
我们的优化将选择最合适的前传链路,以满足天线需求的时延要求。事实上,约束条件(4)规定了在天线与边缘数据中心之间所选通信链路上 的传输延迟L_ij不得超过预期延迟l_i。因此,

as shown in Fig. 3,只有预期延迟将保留在最终解中。这由以下不等式保证:
$$
L_{ij} \times x_{ij} \le l_i, \quad \forall i \in I, \forall j \in J \tag{4}
$$
约束条件(5) 确保如果至少有一个天线被分配给边缘数据中心 j(即 ∑i ∈ I x_ij ≥1),则该边缘数据中心被激活(即 y_j = 1 ),并且只要其 处理能力未超过,就可以用于托管其他天线。我们回顾一下,当天线需 求到边缘数据中心的最优分配达到所使用的边缘数据中心数量最少时, 即为最优。这将帮助网络运营商降低其网络成本。
$$
y_j \le \sum_{i \in I} x_{ij}, \quad \forall j \in J \tag{5}
$$
因此,我们的数学模型由上述ILP公式表征,该公式由目标函数(1) 以及约束条件(2)、(3)、(4)和(5)组成。通过使用分支定界方法[35], , 我们提出的数学模型探索RRH‐BBU分配问题的所有可行解,并选择最 优解,从而确定将可用边缘数据中心中的有限处理资源分配给天线需求 的最优策略。这使得在满足时延要求的同时,通过使用较少数量的边缘 数据中心实现资源利用率提升。
然而,我们所研究的RRH‐BBU分配问题属于NP‐难问题(参见第 3.2节中的证明),因此使用该方法获得最优解所需的收敛时间随着天线 需求数量的增加而呈指数级增长。因此,我们需要研究新的近似算法, 这些算法能够快速收敛,并为大规模问题实例提供最优或近似最优解。
接下来,我们介绍三种启发式算法:(i) 基于拟阵的方法,(ii) b‐匹 配公式,以及 (iii) 基于多背包问题的算法。需要回顾的是,基于ILP公 式的精确方法所得到的解是最优解(“最佳”解),并将用于评估所提 出启发式算法所提供解的质量。
4.2. 基于拟阵的算法
除了基于ILP公式的上述精确模型外,我们还研究了一种新的多项 式时间算法,该算法可扩展到更多的天线和边缘数据中心。由于精确解 能够高效地联合优化延迟和资源分配,我们提出了一种基于拟阵理论的 近似算法,具有类似的性质和准则。
4.2.1. 拟阵背景与构建
接下来,我们通过Korte和Vygen提供的定理[35]来介绍拟阵的定义。
定义 4.1. 一个拟阵 M=(E, F)是一种结构 ,其中 E是有限元素 集 ,且 F是 E 的子集构成的族,满足以下基本性质:
- ∅ ∈ F。
- 若A ∈ F且B⊆ A,则B ∈ F。
- 若A,B ∈ F,且 | B | > | A | ,于是 ∃ e ∈ B\A,使得A ∪{ e} ∈ F。
如果F仅满足性质(1)和(2),则我们称之为一个独立系统。E的基是 E中的极大集,且拟阵的所有基具有相同的基数。有关拟阵理论的更多 细节可参见[5,36,37] 。
利用图3的二分图 G=( I ∪ J , E) ,RRH‐BBU分配问题的最优解在 于将每个天线需求托管在一个边缘数据中心中。类似地,在二分图 G 中,每个顶点 i ∈ I 将被精确地分配给一个顶点 j ∈ J,且每个顶点 j ∈ J 可以是 I 中不同顶点的邻居,因为每个边缘数据中心可以承载多个天线需求。这产生了一个如图3所示的解,展示 了一片将天线(RRHs)与边缘数据中心(BBU池)进行最优连接的树的森林。因此,我们提出以下定理,该定理使用拟阵理论定义了我们的分配算法。
定理4.1。 设G=(I ∪ J, E)为如图3所示的加权二分图。通过放宽数据 中心的容量限制约束条件,M=(E, F)是一个拟阵,其中 F={ I ⊆ E,I 是树的森林} 。据我们所知,我们的基于拟阵的算法在文献中广为人知(例如见 [5] ),并被称为图拟阵。
证明如下所示:
- 关于拟阵的第一个条件(1) ,在 Definition 4.1中提到的,是平凡 的。
- 定义4.1的第二个条件(2):假设我们有A ∈ F ,并且根据F的定义, A是一片由树构成的森林。因此,如果B⊆ A,则即使从A中删除一条 或多条边,B的连通分量也仍然是树。由此可以很容易地得出结论: B ∈ F。
- 为证明定义4.1的最后条件(3),我们注意到A= ∪ k i= 1 A i,其表示 A的连通分量(树)。然后,对于所有i= 1 ,…,k,假设G i=(T i , A i,其中G i是一棵具有| T i| 个顶点和| A i| 条边的树。由此可推 导出A的顶点数为
$$
n_A = \sum_{i=1}^{k} | T_i | = | A | + k. \tag{6}
$$
我们还假设 B = ∪ t j=1 B j, ,记作 G′ i=(T′ i, B i) ,其中 G′ i 是一棵具有 | T′ i | 个顶点和 | B i| 条边的树。则 B 的节点数 由下式给出:
$$
n_B = \sum_{j=1}^{t} | T’_i | = | B | + t. \tag{7}
$$
通过使用 | B | > | A | ,讨论了两种情况:
- 如果 n_B > n_A (t > k):我们假设 B 比 A 能到达更多的 顶点,因此存在一个由 B 覆盖但未被 A 覆盖的顶点x。假设 e ∈ B 是一条包含顶点x作为其两个端点之一的边,我们最终 可推导出 A ∪{ e} ∈ F。
- 如果 n_B < n_A:我们假设 B 中的边将 A 中同一连通分量 (树)A_i 内的每一对节点连接起来。通过反证法,我们假设 不存在边 e ∈ B\A,从而得到 A ∪{ e} ∈ F。这意味着:边e ∈ B,连接同一分量(树)A_i 中的两个顶点并形成一个环。在这种情况下,B的边数将满足 | B |≤| V_1 | + | V_2 | +…+ | V_k| , 则 | B| ≤| A| ,这与我们的假设| B| > | A| 矛盾。
由定理4.1给出的拟阵公式未考虑边缘数据中心的容量限制约束,而 这些约束在我们的RRH‐BBU分配问题中非常重要。事实上,这些约束 会影响用于承载天线需求的边缘数据中心的选择。为了在解中引入这些 约束条件,我们提出对基于拟阵的算法进行简单修改,如下所示。
4.2.2. 基于拟阵的算法的复杂性
评估我们提出的基于拟阵的算法( 算法 1 )的复杂性至关重要。 我们注 意到,该算法的复
该问题为NP‐难,且我们需要快速且成本高效的方法来应对这种复杂性。我们提出的基于拟阵的算法(如算法1所述),其全局复杂度(最坏 情况下)为 O( m ln(m)+ m) ,其中 m ln (m) 表示根据权重(在本 例中为延迟)对 m 条边的集合进行排序的复杂性,而算法1中指出的 “For”循环迭代 m 次。
算法 1 用于 RRH‐BBU 分配问题的基于拟阵的算法。
放置 A= ∅ ;
l_e1 ≤ l_e2 ≤ ... ≤ l_em;
for i= 1到 m do
如果 A ∪{ e_i} ∈ F则
如果 c_I(ei) ≤ C_T(ei)则
A:= A ∪{ e_i}
C_T(ei) −= c_I(ei)
结束 if
结束 if
结束 for
其中 e_i 是边缘 e_i 上的通信延迟;I(ei) (分别地 T(ei) )表示边缘 e_i 的起始(分别地 终端)端点;c_I(ei) 表示处理天线需求 I(ei) 所需的CPU核心数;C_T(ei) 表示边缘数据中心 T(ei) 中的可用CPU数量。
除了基于拟阵的算法外,我们接下来还引入另一种基于b‐匹配方法 的启发式算法。该方案旨在在满足所有天线需求的前提下,寻找RR Hs与BBUs之间的最优映射。通过使用b‐匹配算法,我们希望快速获得 大规模RRH‐BBU分配问题的最优解或近似最优解。而当拟阵方法面对 较大的天线需求(超过100根天线)以及可用边缘数据中心的计算资源 有限时,可能难以实现这一目标。
4.3. b-匹配算法
为了解决更大规模的问题实例,我们提出了一种基于b‐匹配理论的 新启发式方法,以在可忽略的时间内获得最优或近似最优解。所提出的 启发式方法考虑了第3.1节中描述的二分图,并通过寻找最小权重b‐匹配 来快速将天线需求分配给可用边缘数据中心。以下[35]中介绍了b‐匹配 问题的定义:
定义4.2。 设G是一个具有整数边容量u : E(G) → N ∪ { ∞}和数值b : V(G) → N 的无向图。则( G, u)中的一个b‐匹配是函数f : E(G) → Z + ,满足对所有 e ∈ E(G)有f(e)≤u(e),且对所有v ∈ V(G)有 ∑ e ∈ δ(v) f(e) ≤b(v)。其中 V ( G )(resp. E ( G )) 表示 图 G 中顶点的集合(resp. 边集),而 δ(v) 是 顶点 v 的关联边集 。 v 。
根据此定义,我们引入一种新算法,通过在二分图 G=(I ∪ J, E) 中寻找最小权重b‐匹配来解决约束资源分配问题。该算法将联合考虑延 迟约束和边缘数据中心的容量约束。
命题 4.2。 设 G=(I ∪ J, E)为如图 3 所示的加权二分图 。 RRH-BBU 分配问题可通过寻找最小权重b-匹配并考虑以下参数来求解:
- 边上的整数容量 : u = 1 。
- b(v) = 1 , ∀ v ∈ I(I 是 一 组 天线 的集合)。
- b(v)= min{| I_v | , ⌊ C_v / c(v) ⌋}, ∀ v ∈ J(J is a set of edge data cen-ters).
其中 :
- I_v 是当天线需求满足预期延迟和每个天线所需的CPU核心数时, 可分配给边缘数据中心 v ∈ J 的天线子集:I_v={ i ∈ I | l_i ≥ L_ij ∧ c_i ≤C_j} 。
- c(v) 是可分配给边缘数据中心 v ∈ J 的天线所需的平均 CPU 核心数:c(v)= ∑ i∈ I_v c_i / | I_v | 。
此外,为了帮助我们的优化找到具有整数变量的最优解,我们添加 了由以下公式给出的blossom不等式:
$$
\sum_{e \in E(G[X])} x_e+ \sum_{e \in F} x_e \le \left\lfloor \frac{1}{2}\left( \sum_{v \in X} b(v)+ | F | \right) \right\rfloor, \quad \forall X \subseteq I \cup J, F \subseteq \delta(X) \tag{8}
$$
其中 E(G[X]) 表示由顶点集 X 生成的子图 G(X) 中边的子集,δ(X) 是 X 的关联边集合(更多细节见 [35,38] )。
最后,我们利用所得到的命题 4.2的结果,提出一种新的最小权 重<b‐匹配模型,以多项式时间求解 RRH‐BBU(射频拉远单元‐基带处 理单元)分配问题。该数学<formu‐ formulation由以下模型给出:
$$
\min F= \sum_{e \in E} L_e \times x_e
$$
S.T.:
$$
\
该问题为NP‐难,且我们需要快速且成本高效的方法来应对这种复杂性。我们提出的基于拟阵的算法(如算法1所述),其全局复杂度(最坏 情况下)为 $O( m \ln(m)+ m)$ ,其中 $m \ln (m)$ 表示根据权重(在本 例中为延迟)对 $m$ 条边的集合进行排序的复杂性,而算法1中指出的 “For”循环迭代 $m$ 次。
算法 1 用于 RRH‐BBU 分配问题的基于拟阵的算法。
放置 A= ∅ ;
l_e1 ≤ l_e2 ≤ ... ≤ l_em;
for i= 1到 m do
如果 A ∪{ e_i} ∈ F则
如果 c_I(ei) ≤ C_T(ei)则
A:= A ∪{ e_i}
C_T(ei) −= c_I(ei)
结束 if
结束 if
结束 for
其中 $e_i$ 是边缘 $e_i$ 上的通信延迟;$I(e_i)$ (分别地 $T(e_i)$ )表示边缘 $e_i$ 的起始(分别地 终端)端点;$c_{I(e_i)}$ 表示处理天线需求 $I(e_i)$ 所需的CPU核心数;$C_{T(e_i)}$ 表示边缘数据中心 $T(e_i)$ 中的可用CPU数量。
除了基于拟阵的算法外,我们接下来还引入另一种基于b‐匹配方法 的启发式算法。该方案旨在在满足所有天线需求的前提下,寻找RR Hs与BBUs之间的最优映射。通过使用b‐匹配算法,我们希望快速获得 大规模RRH‐BBU分配问题的最优解或近似最优解。而当拟阵方法面对 较大的天线需求(超过100根天线)以及可用边缘数据中心的计算资源 有限时,可能难以实现这一目标。
4.3. b-匹配算法
为了解决更大规模的问题实例,我们提出了一种基于b‐匹配理论的 新启发式方法,以在可忽略的时间内获得最优或近似最优解。所提出的 启发式方法考虑了第3.1节中描述的二分图,并通过寻找最小权重b‐匹配 来快速将天线需求分配给可用边缘数据中心。以下[35]中介绍了b‐匹配 问题的定义:
定义4.2。 设$G$是一个具有整数边容量$u : E(G) \to \mathbb{N} \cup { \infty}$和数值$b : V(G) \to \mathbb{N}$ 的无向图。则$( G, u)$中的一个b‐匹配是函数$f : E(G) \to \mathbb{Z}^+ $,满足对所有 $e \in E(G)$有$f(e)\le u(e)$,且对所有$v \in V(G)$有 $\sum_{e \in \delta(v)} f(e) \le b(v)$。其中 $V(G)$(resp. $E(G)$) 表示 图 $G$ 中顶点的集合(resp. 边集),而 $\delta(v)$ 是 顶点 $v$ 的关联边集。
根据此定义,我们引入一种新算法,通过在二分图 $G=(I \cup J, E)$ 中寻找最小权重b‐匹配来解决约束资源分配问题。该算法将联合考虑延 迟约束和边缘数据中心的容量约束。
命题 4.2。 设 $G=(I \cup J, E)$为如图 3 所示的加权二分图 。 RRH-BBU 分配问题可通过寻找最小权重b-匹配并考虑以下参数来求解:
- 边上的整数容量 : $u = 1$ 。
- $b(v) = 1$, $\forall v \in I$($I$ 是一组天线的集合)。
- $b(v)= \min{| I_v |, \left\lfloor C_v / c(v) \right\rfloor}$, $\forall v \in J$($J$ 是一组边缘数据中心)。
其中 :
- $I_v$ 是当天线需求满足预期延迟和每个天线所需的CPU核心数时, 可分配给边缘数据中心 $v \in J$ 的天线子集:$I_v={ i \in I \mid l_i \ge L_{ij} \land c_i \le C_j}$ 。
- $c(v)$ 是可分配给边缘数据中心 $v \in J$ 的天线所需的平均 CPU 核心数:$c(v)= \sum_{i\in I_v} c_i / | I_v |$ 。
此外,为了帮助我们的优化找到具有整数变量的最优解,我们添加 了由以下公式给出的blossom不等式:
$$
\sum_{e \in E(G[X])} x_e+ \sum_{e \in F} x_e \le \left\lfloor \frac{1}{2}\left( \sum_{v \in X} b(v)+ | F | \right) \right\rfloor, \quad \forall X \subseteq I \cup J, F \subseteq \delta(X) \tag{8}
$$
其中 $E(G[X])$ 表示由顶点集 $X$ 生成的子图 $G(X)$ 中边的子集,$\delta(X)$ 是 $X$ 的关联边集合(更多细节见 [35,38] )。
最后,我们利用所得到的命题 4.2的结果,提出一种新的最小权 重b‐匹配模型,以多项式时间求解 RRH‐BBU(射频拉远单元‐基带处 理单元)分配问题。该数学模型由以下模型给出:
$$
\min F= \sum_{e \in E} L_e \times x_e
$$
S.T.:
$$
\sum_{e \in \delta(v)} x_e= 1, \quad \forall v \in I;
$$
$$
\sum_{e \in \delta(v)} x_e \le \min\left{| I_v |, \left\lfloor \frac{C_v}{c(v)} \right\rfloor\right}, \quad \forall v \in J;
$$
$$
\sum_{e \in E(G[X])} x_e+ \sum_{e \in F} x_e \le \left\lfloor \frac{1}{2}\left( \sum_{v \in X} b(v)+ | F | \right) \right\rfloor, \quad \forall X \subseteq I \cup J, F \subseteq \delta(X);
$$
$$
x_e \in \mathbb{R}^+, \quad \forall e \in E; \tag{9}
$$
4.3.1. b-匹配算法的复杂性
为了评估b‐匹配算法在合理时间内为大规模图实例找到优质解的能力, 我们在本节中分析所提出算法的复杂性。我们注意到,该算法的目标是在 严格的延迟要求和有限的处理能力约束条件下,将天线需求分配给可用边 缘数据中心。我们提出的线性规划或b‐匹配解的复杂性为$O(| V | | E|^2 \ln (| V |^2 / | E|))$ ,其中$V = I \cup J$,$E$是$I$与$J$之间加权链路的集合。该方法 是一种简单的线性规划,其复杂性可忽略不计。感兴趣的读者可在[39]中 找到更多细节。
接下来,我们介绍另一种使用多背包问题建模的启发式算法。如前 所述,多背包方法已在不同场景下被广泛用于解决资源分配问题。在 C‐RAN背景下,我们提出一种基于多背包问题建模的改进算法,以解决 RRH‐BBU分配问题。该算法所提供的解将与拟阵、b‐匹配和ILP算法进 行对比,以便在不同的仿真场景和性能指标下更好地评估我们算法的性 能。
4.4. 基于多背包的算法
在本节中,我们提出了一种基于多背包问题建模的近似算法。实际 上,多背包问题建模是将经典背包问题 $(KP)$ 从单个背包推广到具有不 同容量的 $m$ 个背包。多背包算法的目标是将每个物品至多分配给一个背 包,使得不违反任何容量约束条件,并且放入背包中的物品总利润最大 化。以下定义中介绍了多背包算法。
定义 4.3。 给定 $n$ 个物品的集合和 $m$ 个背包的集合($m < n$),其中 $p_j=$表示物品 $j$ 的利润,$w_j=$表示物品 $j$ 的重量,$c_i=$表示背包 $i$ 的容量,目标是找到 $m$ 个互不相交的物品子集,使得所选物品的总利润 最大,并且每个子集可以分配到不同的背包中,且背包的容量不小于该 子集中物品的总重量。
根据此定义,并结合图3中描述的二分图 $G=(I \cup J, E)$ ,我们得到 本文所讨论的约束资源分配问题与多背包问题建模之间的如下等价关系:
- 背包是边缘数据中心($j \in J$)。
- 天线需求($i \in I$)是需被插入到背包(数据中心)中的物品 。
- 重量 $w_j$是处理天线需求 $i$所需的CPU核心 $c_i$的数量。
- 利润 $p_j$在不同的天线需求之间不变化 ,并可设为 1($p_j = 1$)。
该建模方法仅关注边缘数据中心的处理能力,而未考虑天线需求的 时延要求,从而解决我们的资源分配问题。延迟约束的放宽会影响选择 哪个边缘数据中心来承载天线需求。因此,为了在解中考虑这些约束条 件,我们对多背包算法引入了一个简单的修改,即在将天线需求分配给 边缘数据中心之前,检查预期延迟是否得到保证。我们在算法2中展示 了多背包问题建模。
算法2
改进的多重背包算法。
输入:$G=(I \cup J, E)$, 天线需求, 边缘数据中心。
输出:所有天线需求在可用边缘数据中心上的联合映射(CPU, 延迟)。
具体步骤如下:
步骤1:将边缘数据中心($j \in J$)按其 CPU 容量 $C_j$ 升序排列;
步骤2:通过检查是否满足条件,选择可分配给选定边缘数据中心 $j$ 的天线需求:
• 天线需求的预期延迟由将其连接到所选边缘数据中心$j$的通信链路提供;
• 所选边缘数据中心$j$中的可用计算资源大于该天线需求请求的CPU核心数;
步骤3:使用动态规划方法将尽可能多的天线需求分配给所选边缘数据中心(例如见[40]);
步骤4:更新所选边缘数据中心中可用CPU核心的总数;
步骤5:重复步骤2、3和4,直到所有考虑的天线需求都被分配到边缘数据中心。
5. 性能评估
仿真和实验使用优化求解器CPLEX [40] 来处理线性规划方法、基于ILP公式(第4.1节)的精确算法以及b‐匹配公式(见第4.3节公式(9))。我们首先评估精确算法的性能,然后从收敛时间、可扩展性和最优性方面将所获得的解(最优解)与启发式算法得到的解进行比较。每个仿真场景使用不同的参数运行100次。
5.1. 仿真设置与参数
我们的算法性能评估是在一台2.40 GHz、8GB内存的PC上进行的。天线数量根据参数为$\lambda \times \text{空间_维度}$的泊松过程生成,其中$\lambda$在范围 $[0.1; 1]$内变化,空间_维度在范围$[5; 20]$内变化。
在图 4中,我们展示了四种仿真场景的示例,这些场景考虑了一个区域为空间_维度= 10 × 10的蜂窝网络,并且天线密度分别为$\lambda \in {0.3; 0.5; 0.8; 1}$。
每根天线包含来自终端用户的随机数量的需求,以[5;10]区间内的 CPU核心数量表示(一些论文如[16,41]考虑物理资源块PRB的分配, 但这不会改变我们的数学建模以及算法向优质解的收敛性)。边缘数据 中心数量设置为20个,每个边缘数据中心具有随机的计算资源(可用 CPU核心数量),取值范围为[50;200] CPU核心。天线需求的工作负载 (即以等效CPU核心表示的终端用户需求的聚合量)要求延迟不超过1 毫秒,该延迟值在[0.1;1]毫秒范围内随机生成。为了清晰起见,我们在 表2中总结了仿真设置和参数。
| 参数 | 值 |
|---|---|
| 天线密度 $\lambda$ | $\in[0.1;1]$ |
| 空间维度 | 10 × 10; 20 × 20;… |
| 泊松参数 | $\mu = \lambda \times \text{空间_维度}$ |
| 天线数量 | 泊松分布:$P(\mu)$ |
| 天线坐标 | 均匀分布:$U(0,\text{空间_维度})$ |
| 边缘数据中心数量 | 20 |
| 天线 $i$ 与边缘数据中心 $j$ 之间的延迟 | 5 μ秒/千米 |
| 天线 $i$ 的预期延迟 $l_i$ | $\in[0.1 \text{毫秒}; 1 \text{毫秒}]$ |
| 每个天线所需的CPU核心数 $c_i$ | $\in[5; 10]$ |
| 每个边缘数据中心$j$的CPU核心数 $C_j$ | $\in[50;200]$ |
5.2. 性能指标
用于评估我们算法(精确算法和启发式算法)性能的指标如下所述:
- 收敛时间 :指算法收敛到其最优解所需的时间。
- 资源利用率 :定义为用于承载聚合天线需求的边缘数据中心所占的 百分比,可表示如下:其中$| J|$ 为可用边缘数据中心的总数。
$$
\text{Resource utilization rate}(\%)= \frac{\sum_{j \in J} y_j}{| J |} \times 100 \tag{10}
$$
- 差距 :用于将所提出的启发式算法与作为“参考和最优解”的精确ILP算法进行基准比较。在不失一般性的前提下,我们重点关注 CPU资源消耗的对比(以用于承载所有天线需求的边缘数据中心百分比表示)。需要注意的是,当成本差距值越小时,启发式算法所提供的解的质量越好(当差距等于0时达到最优)。该指标正式表达为:
$$
\text{Gap}(\%)= \frac{| \text{Utilization rate (ILP)} - \text{Utilization rate (Heuristic)} |}{\text{Utilization rate (ILP)}} \times 100 \tag{11}
$$
- Rejection rate : 指无法分配到每个边缘数据中心的天线需求的平均百分比。该指标可表示为决策的函数
$$
\text{Rejection rate}(\%)= \frac{| I | - \sum_{j \in J} \sum_{i \in I} x_{ij}}{| I |} \times 100 \tag{12}
$$
其中 $| I |$ 是天线的总数。
- SLA违规率 :就CPU核心而言超用的边缘数据中心的平均值。该指标将主要用于评估基于拟阵的方法在寻找不违反边缘数据中心的容量限制约束(在ILP公式中由约束条件(3)定义)的最优解方面的能力。我们仅关注基于拟阵的算法(如定理4.1所定义),因为在 ILP、b‐匹配和多背包方法中不存在SLA违规。SLA违规率的平均值可以表示为决策变量(第4.1节)和参数(见表1)的函数。
$$
\text{SLA violations rate}(\%)= \frac{1}{| J |} \sum_{j\in J} \frac{\sum_{i \in I} c_i \times x_{ij} - C_j \times y_j}{C_j \times y_j} \times 100 \tag{13}
$$
其中 $| J |$ 是可用的边缘数据中心的总数。
| 空间 | $\lambda$ | 天线数量 | 收敛时间 | 拒绝率 |
|---|---|---|---|---|
| 10 × 10 | 0.3 | 30 | 9.63秒 | 0 |
| 10 × 10 | 0.5 | 50 | 10.92秒 | 0 |
| 10 × 10 | 0.8 | 80 | 11.87秒 | 0 |
| 10 × 10 | 1 | 100 | 12.58秒 | 0 |
| 20 × 20 | 0.3 | 120 | 62.09秒 | 0 |
| 20 × 20 | 0.5 | 200 | 86.56秒 | 0 |
| 20 × 20 | 0.8 | 320 | 2.87分钟 | 0 |
| 20 × 20 | 1 | 400 | 4.39分钟 | 0 |
5.3. 性能分析
5.3.1. 基于整数线性规划方法的性能评估
表3描述了基于ILP公式的精确算法在收敛时间和拒绝率方面的性能 结果。该算法在找到最优解之前会遍历所有可行解,导致当增加天线数量时,收敛时间呈指数级增长。事实上,对于包含400根天线和20个可用边缘数据中心的实例,ILP方法需要超过4分钟(4.39分钟)才能收敛到最优解。这是预料之中的,因为所研究的问题是NP‐难的。因此, ILP方法仅适用于天线数量不超过100的小规模或中等规模实例。此外, 拒绝率始终等于0,这意味着基于整数线性规划公式化的方法始终能够将所有天线需求分配至可用的 边缘数据中心。
5.3.2. 启发式算法的性能评估
在表4中,我们通过改变所考虑的空间区域的尺寸以及部署的天线密度来构建不同的仿真场景(见图4中的示例)。通过这些仿真,我们希望 评估所提出的近似算法的性能:基于拟阵的算法(算法1)、由式(9)给出的b‐匹配公式以及基于多背包的方法(算法2)。
如表4所示,我们的启发式算法与提供最优解的ILP方法进行了基准 比较,使用了三个性能指标:收敛时间、差距(11)(用于与精确方法 提供的最优解进行比较)以及拒绝率(12)。我们注意到,仅当拒绝率为0时才计算差距,否则该差距并无实际意义。
表4清楚地突显了基于拟阵的算法在寻找近似最优解方面的效率, 其速度优于基于ILP公式的精确方法。事实上,在最坏情况下,基于拟阵的方法提供的解平均差距不超过7%,并且在考虑包含400根天线和 20个可用边缘数据中心的大规模图时,仅需2毫秒即可收敛。因此,基于拟阵的方法可用于应对大规模问题实例。
然而,拟阵方法存在一些缺点,例如无法为大规模问题实例分配所有天线需求。这一点通过拒绝率指标得以体现,对于包含400根天线和 20个边缘数据中心的实例,其拒绝率可能达到19%。
为了更好地评估我们基于拟阵的算法的性能,我们在增加考虑的边缘数据中心数量时计算了拒绝率。为此,我们考虑了两个分别具有320 和400根天线的网络实例,并将边缘数据中心的数量从20调整到60。这些仿真得到的结果由图5表示。

仿真 结果 在 图5 中显示 , 拒绝率 取决于 可用的计算资源数量 , 因此当可用边缘数据中心数量增加时,拒绝率下降。 事实上, 对 于第一个仿真场景 (320 根天线),基于拟阵的算法在有至少40个可用边缘数据中心时,拒绝率等于0;而在第二个仿真场景(400根天线)中,当有至少50个可用边缘数据中心 时,拒绝率消失。这意味着,当考虑更多资源(边缘数据中心)时,基于拟阵的算法变得更加高效。
此外,为了更好地了解基于拟阵的方法的相对性能,我们在图6中 展示了不同网络规模下的SLA违规率表现。实际上,我们考虑了四种仿真场景:将50、100、200、320根天线高效分配给数量从20到100个的 边缘数据中心。需要说明的是,在此仿真中,我们采用定理4.1中定义的 基于拟阵的算法,并在放松边缘数据中心的容量限制约束条件下进行; 同时,我们根据公式(13)定义的方式计算SLA违规率。
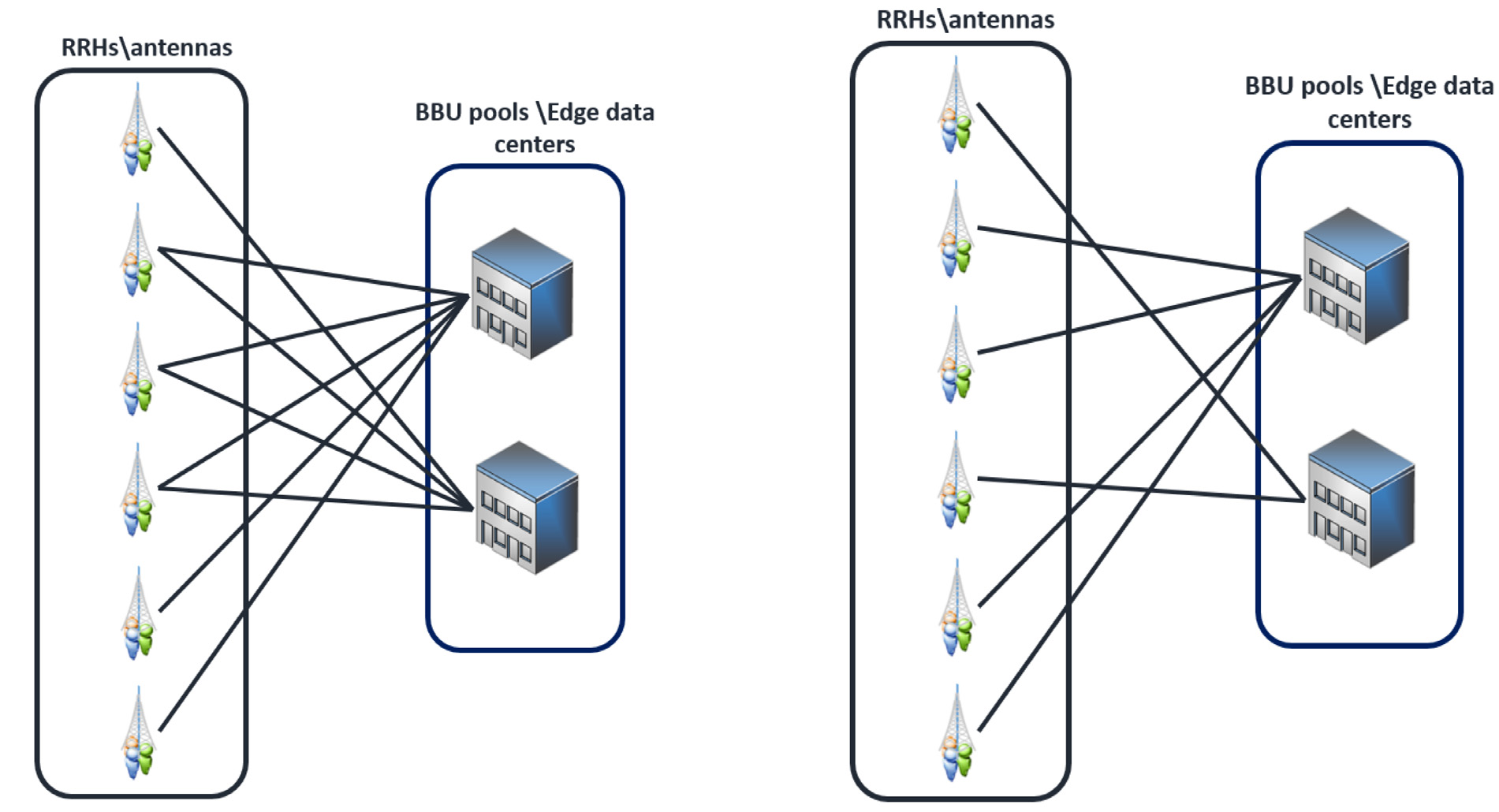
图6中的仿真结果证实,当考虑更多的处理资源(边缘数据中心) 时,SLA违规率会降低。这表明基于拟阵的算法的效率取决于可用处理 资源的数量,并且在使用更多资源(边缘数据中心)时能够获得良好的 解。
5.3.3. 资源利用率行为
图7展示了三种近似算法(拟阵、b‐匹配和多背包)以及ILP方法在 资源利用率百分比(以使用的边缘数据中心数量衡量)方面的表现。尽管ILP方法具有微弱优势,即在保留最优解之前会考察所有可行解,但 基于拟阵的方法和b‐匹配算法仍能在将天线需求高效分配给可用边缘数据中心方面表现出色,而多背包算法所得解消耗的边缘数据中心数量较多(如图7 a所示)。
需要指出的是,对于更大规模的问题实例(图7 b),与拒绝率为 0%的整数线性规划解相比,b‐匹配算法在资源利用率方面始终能提供接近最优的解。然而,对于拟阵和多背包算法而言,在网络规模较大时 (见图7 b),其资源利用率取决于拒绝率(虽然可忽略但不为零)。因此,我们推断当考虑更大规模的问题实例时,b‐匹配算法能够轻松扩展, 因而可被网络运营商用于有效降低其网络成本(资本支出和运营支出) 并实现网络利用率增益。

5.3.4. 算法性能评估使用真实 traces
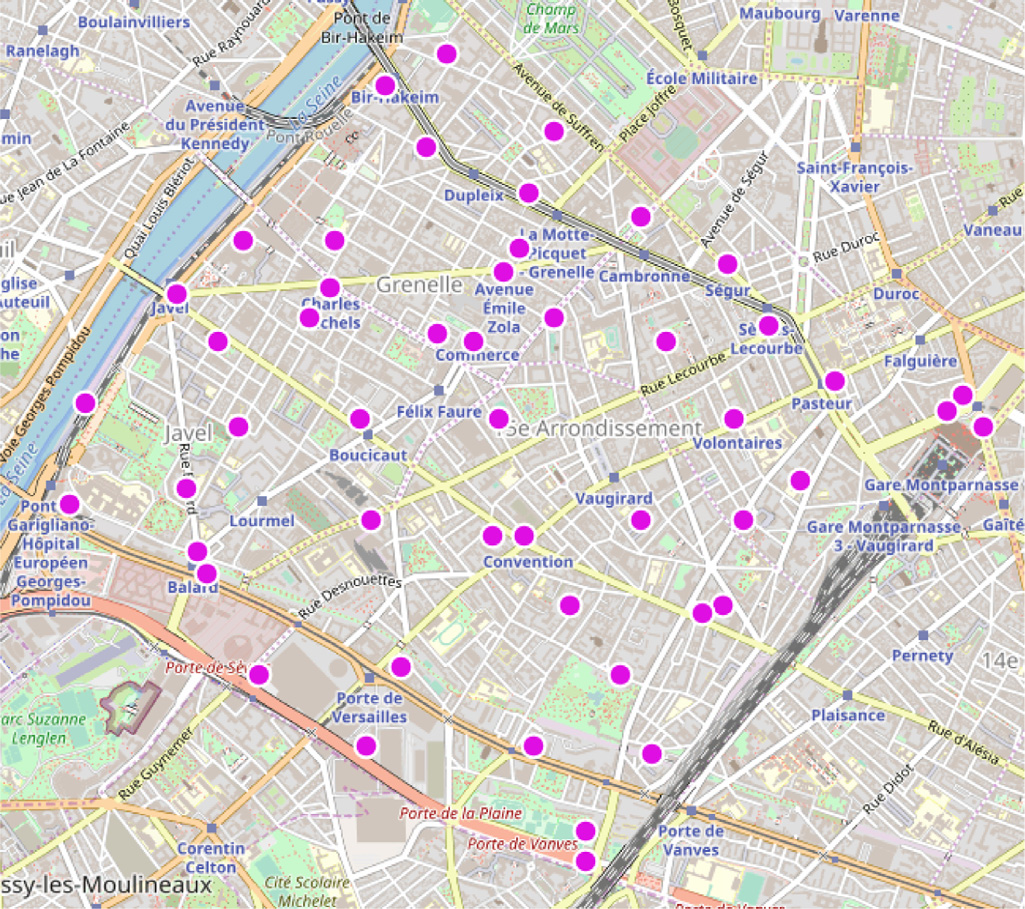
为了更好地评估我们所提出算法的性能,我们考虑了网络运营商 Orange在巴黎某小区域内的4G‐LTE小区地图的真实轨迹[42] 。如图8 所示,该拓扑结构表示一个包含50个天线及其给定地理位置(坐标)的 蜂窝网络。然后,根据陈及其合作者[2,24],的方法,我们在小区地图上 布置了20个边缘数据中心,使得天线与边缘数据中心之间的距离在20至 40公里之间。类似于表2中描述的仿真参数,我们认为每个边缘数据中心 具有以CPU核心衡量的有限处理容量,而天线需求则具有可变的处理和 时延要求。
在本实验中,我们将基于ILP公式(如第4节所述)的精确方法以及 三种提出的近似算法应用于图8的4G‐LTE小区地图,这三种近似算法包括基于拟阵的算法(算法1)、b‐匹配公式(9)和多背包方法(算法2)。这些算法所提供的解将根据三个性能指标进行基准测试:收敛时间、由 (10)给出的资源利用率和由(12)定义的拒绝率。
| 算法 | 收敛时间(毫秒) | 资源利用率(%) | 拒绝率(%) |
|---|---|---|---|
| ILP公式 | 334.21 | 15 | 0 |
| b‐匹配算法 | 23.52 | 15 | 0 |
| 基于拟阵的方法 | 0.58 | 15 | 0 |
| 多背包算法 | 1.7 | 25 | 0 |
表5显示,基于拟阵的方法和b‐匹配公式都能在可忽略的时间内提供最优解(与ILP方法提供的相同解)。实际上,基于拟阵的方法以 0.58毫秒收敛到最优解,略占优势,而b‐匹配算法也能在23.52毫秒内 为天线需求向可用边缘数据中心实现高效分配。然而,多背包算法所得 的解消耗了更多的边缘数据中心数量,资源利用率为25%。在拒绝率指标方面,所有提出的算法均能将考虑的所有天线需求分配至可用边缘数据中心,并满足其延迟和处理需求,且无SLA违规。
5.3.5. 可扩展性评估
如果不考虑非常大的问题实例的可扩展性,则性能评估将是不完整的。事实上,我们提出了一个仿真场景,其中包含400根天线和边缘数据中心数量为{60, 80}的实例,二者均根据表2中详述的参数生成。表6中的 仿真结果表明,与ILP方法相比,基于拟阵的方法和b‐匹配算法在可忽略 的时间内高效地找到了良好的解。具体而言,拟阵算法在小于28毫秒的时间内提供了近似最优解(差距不超过2%),而b‐匹配算法可以在小于 4秒的时间内最优求解分配问题(差距值不超过3%)。然而,由于需要 探索所有可行解,ILP方法在超过1小时的时间内仍未收敛。
| 天线数量 | #边缘数据中心 | ILP | b‐匹配 | 拟阵 | 多背包 |
|---|---|---|---|---|---|
| 400 | 60 | 34.28分钟 | 1.47 秒 | 6.42 毫秒 | 82.84 毫秒 |
| 800 | 80 | 1.02小时 | 3.97 秒 | 27.16 毫秒 | 107.4 毫秒 |
5.3.6. 所提算法的比较分析
在本节中,我们对所提出的联合约束资源分配与RRH‐BBU分配问题的算法进行了全面比较。这些方法在以下方面的分类:(i)计算复杂度;(ii)成本节约(包括运营支出和资本支出);(iii)可扩展性; (iv)实现难度,已在表7中突出显示。因此,拟阵和b‐匹配算法在可忽略的时间内找到高质量解以及扩展到更大规模的问题实例方面整体上更 高效。然而,我们注意到由于花不等式(约束8)的实现难度较高,b‐匹配算法(描述于9)并不容易实现。
| 算法 | 复杂性 | 成本节约 | 可扩展性 | 实现难度 |
|---|---|---|---|---|
| 基于整数线性规划的算法 | 指数级 | ★★★★ | ☆☆☆☆ | ★★★☆ |
| b‐匹配算法 | 多项式 | ★★★☆ | ★★★☆ | ★★★☆ |
| 基于拟阵的算法 | 对数级 | ★★★☆ | ★★★★ | ☆☆☆☆ |
| 多背包算法 | 线性 | ★☆☆☆ | ★★★☆ | ★★☆☆ |
6. 结论
本文中,我们研究了RRH‐BBU分配问题,旨在确定将天线需求分配给可用边缘数据中心的最佳策略,同时联合优化通信延迟和资源消耗。为此,我们提出了一种基于ILP公式的精确算法,以求解小规模和中等 规模网络的最优解。该精确算法通过将天线需求分配给最合适的边缘数据中心,来优化资源消耗(以使用的边缘数据中心数量衡量)以及相关的通信延迟。然而,该算法在处理大规模问题实例时难以扩展。因此, 我们提出了三种近似算法:基于拟阵的方法、b‐匹配算法和基于多背包 的算法,以在可忽略的时间内满足更大数量的天线需求。
性能评估使用了不同的仿真场景以及巴黎一个小区域内的真实 4G‐LTE蜂窝网络。根据多个性能指标,仿真结果揭示了基于拟阵的方 法和b‐匹配算法相较于多维背包问题公式化方法(文献中最常用的解决 约束资源分配问题的方法)的效率,以及它们即使在大规模问题实例下 也能快速找到最优或近优解的能力。当考虑来自4G‐LTE小区地图的真 实轨迹时,数值结果也证实了这一点。
作为未来工作,我们将考虑边缘数据中心中天线需求的处理延迟 (计算延迟)。事实上,为了简化问题,我们仅考虑了连接天线与边缘 数据中心的前传网络上的通信延迟(传输延迟),以在C‐RAN背景下建 模我们的RRH‐BBU(射频拉远单元‐基带处理单元)分配。进一步考虑 位于边缘数据中心内的BBU执行不同功能所需的BBU处理时间将非常有意义。这可能导致需要高效优化的非线性目标函数。该问题变得更加复杂,需要基于拉格朗日松弛等方法进行深入研究。此外,连接天线与 BBU池的前传网络上的数据流量可以使用不同的协议传输,包括CPRI 和OBSAI。前传网络可以通过不同的方式实现技术,例如光纤通信、标准无线通信或毫米波通信 [43] 。可以研究这些协议和技术的影响,以更好地评估我们提出的模型和算法的性能。




















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








