杨氏矩阵算法详细解释(C语言)

最新推荐文章于 2024-05-31 04:49:18 发布

原创最新推荐文章于 2024-05-31 04:49:18 发布 · 261 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c语言 #启发式算法 #visual studio

这篇博客介绍了如何在一个每一行和每一列都递增的数字矩阵中查找特定数字的算法，该算法利用了矩阵的特性，通过比较右上角元素与目标数字的大小来快速定位，时间复杂度小于O(N)。示例代码展示了如何在3x3的矩阵中查找数字7，并成功找到了其位置。

题目内容:
有一个数字矩阵，矩阵的每行从左到右是递增的，矩阵从上到下是递增的，请编写程序在这样的矩阵中查找某个数字是否存在。

要求:时间复杂度小于O(N);

类似这样的矩阵：

1 2 3
4 5 6
7 8 9

算法解释：

①如果找的数字是7，先与右上角3比较，3<7 排除第一行，下移一行。

②再与第二行最右边的6比较 6<7，排除第二行，再下移一行。

③再与第三行最右边的9比较 9>7 排除第三列。

④左移一列,再与第二列的最下边的8比较 8>7 排除第二列再左移一列。
⑤与最后一个元素7比较 7 = 7符合条件返回值1。

图解如下:

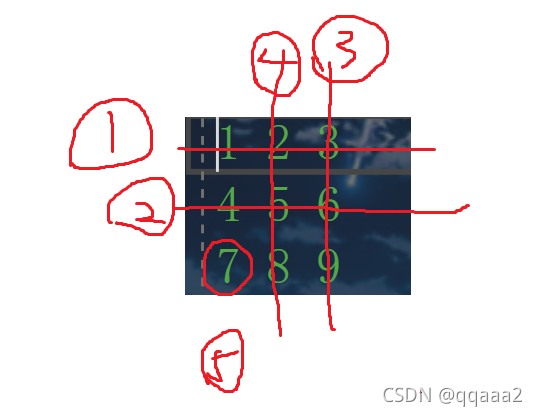
代码如下:

#include<string.h>
#include<stdio.h>
FindNum(int arr[3][3], int k, int* row, int* col)
{
	int x = 0;//第一行
	int y = *col - 1;//第三列
	while (x <= *row - 1 && y >= 0)
	{
		if (arr[x][y] > k)//右上角的元素比我要找的元素k要大,排除掉右上角这一列
		{
			y--;//左移一列
		}
		else if (arr[x][y] < k)//右上角元素小于k,说明不在右上角这一行
		{
			x++;//下移一行
		}
		else
		{
			*row = x;//通过地址改掉了x,y的值
			*col = y;
			return 1;
		}
	}
	//找不到
	return 0;
}
int main()
{
	int arr[3][3] = { {1,2,3}, {4,5,6},{7,8,9} };
	int k = 7;//要查找的数是7
	int x = 3;
	int y = 3;

	//返回型参数 这个参数可以带回来一些值 
	int ret = FindNum(arr, k, &x, &y);//传地址可以改变x,y的值
	if (ret == 1)
	{
		printf("找到了\n");
		printf("下标是:[%d][%d]", x, y);
	}
	else
	{
		printf("没找到\n");
	}
	return 0;
}