首先，二叉树有两种存储方式昂，一种是顺序存储，还有一种是链式存储。
- 顺序二叉树：适用于完全二叉树（含满二叉树）。其优势是存储紧凑、访问子节点/父节点可通过公式直接计算（无需指针），效率高，常用于实现堆、优先队列等数据结构。
- 链式二叉树：适用于非完全二叉树。其优势是存储空间灵活，插入、删除节点时无需移动大量元素，能高效处理树结构的动态变化，是二叉树最通用的存储方式，如二叉搜索树、AVL树等多采用链式存储。
顺序二叉树：
看到了嘛，顺序二叉树一般适用于完全二叉树，而且呢，他的物理存储其实是数组！像树一样的，那只是它的逻辑结构！
如图
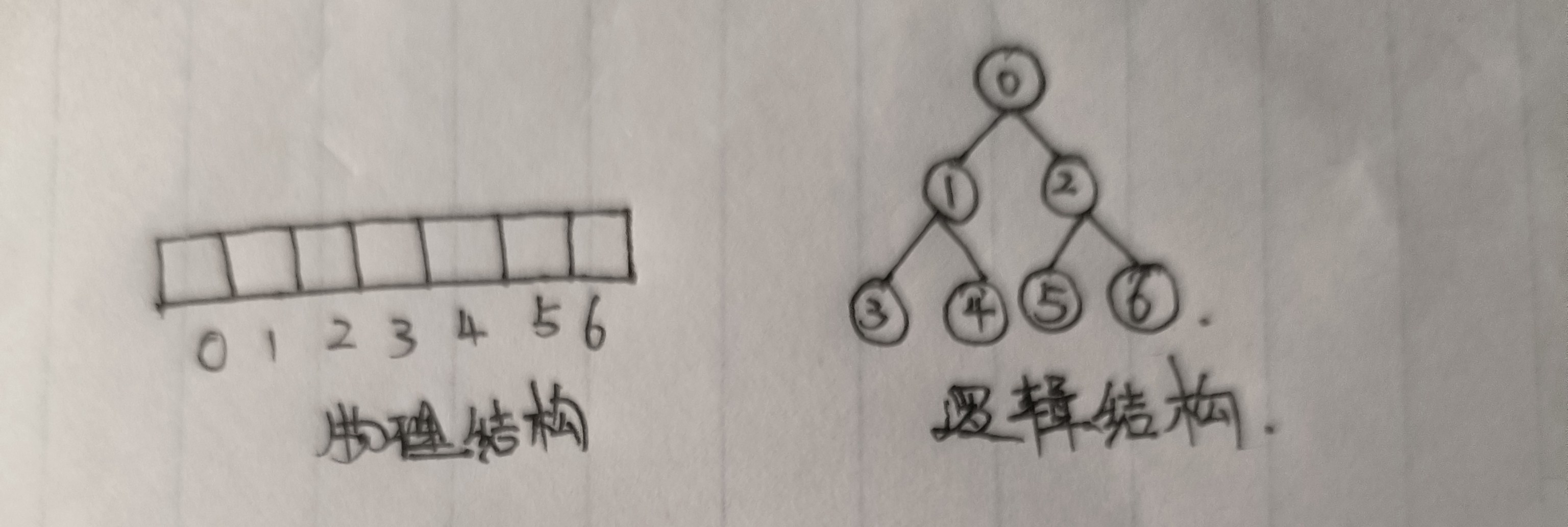
其实他就是把一个数组，给逻辑化看作了 一棵树，并且他们父子节点下标还是有关系的昂！
左孩子＝父节点×2+1
右孩子＝父节点×2+2
父节点＝（子节点-1）÷2
这只在顺序二叉树中可以用昂，好兄弟
那么这种数组二叉树能干什么呢？自此衍生出来了，堆。堆，分为大根堆和小根堆，那就很简单呀，大根堆大根堆，那就是大根呀，也就是他的根节点是最大的，然后依次减小，保证他的父节点比两个子节点都大就好啦，小根堆反之也是。
好了，那么知道大根堆，小根堆后，咱应该怎么建堆呢？或者说如何调整堆嘞？
我有以下两个仙法，哈哈哈哈，向上调整和向下调整。
向上调整是什么？向下调整又是什么呢？
向上调整，那就顾名思义呀，往上调呗，比如新插入一个节点，要这个堆（此处举例为大根堆）仍然有序，是不是需要调整一下呢？一般都是都把数据直接插在最末尾，所以他现在是子节点呀，那他是不是有可能比父节点大呢？对呀！就跟父节点比一比呗，老登，凭啥你是父节点呢？咱俩碰碰呗，所以这个节点和父节点比一比，由此得名，向上调整。下面儿是向上调整的代码实现
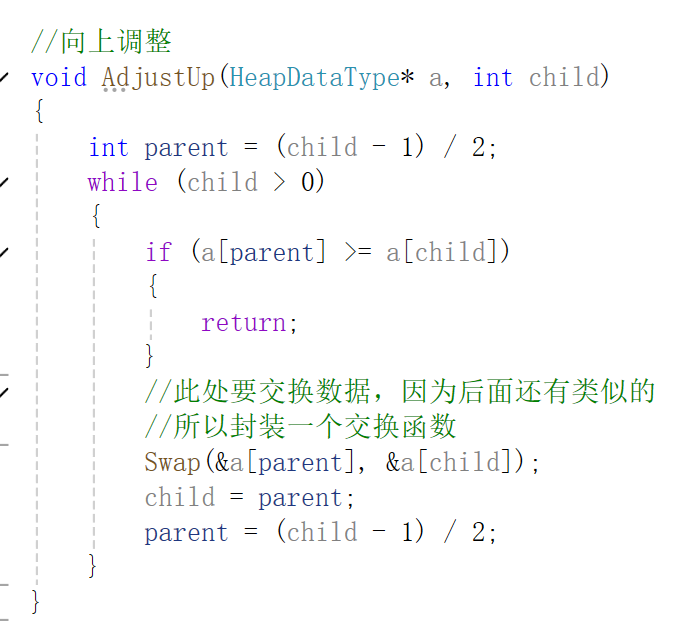这个对交换函数的封装
那向下调整又是什么呢？向下调整就是找到最后一个非叶节点，然后比较他和他的孩子大小呗，先比较比较他滴左右孩子，找大的再和那个非叶结点，也就是父节点，比较大小呗，如果孩子大，那不就把老爸往下调整调整，让他往下稍一稍，这不就是向下调整啦？
但是一般建好的堆不用调整嘞，要是咱要删除一个节点，那不就把它和最后一个节点换一下位置，做个交换（这个函数上面有封装昂），然后再删除一下Size，再把那个尾节点向下调整一下，不就又是堆排序了嘛
纯享版本排序数组：
向下调整排序数组
一个小总结：向上调整一般用于节点的插入，向下调整就是节点的删除啦。
向上调整向下调整学完了，他们能干啥嘞，当然是排序数组啦，有没有发现在堆（大堆）中，最上面的根节点，是整个堆中最大的呢，小堆则相反昂，所以你是不是可以用他来排序数组嘞。
先调整一下这个数组～他现在a[0]是不是就是最大的啦？然后把a[0]这个数据放数组最后呗，再Size--，然后再对数组进行调整，第一个a[0]是不是又是最大的啦？依次类推，就可以排一个降序数组啦～这比冒泡排序等之前学过的效率都高！而且你再想想，在排序的时候，用向下调整好，还是向上调整效率更高呢？
当然是向下调整啦！因为向下调整是从最上面调整（以满二叉树为例），调整到差倒数第二行，然后和最后一行他们的子节点比较大小就行，所以最后一层的不用调整，而向上调整呢？就是从最后一行开始，最后一个节点依次向上，你想想，那是一个等比数列，最下面一层的节点占总数的50％，所以当然向下调整效率高了！
链式二叉树：
首先是链式二叉树的定义，顺序二叉树是由数组构成的，那么链式二叉树呢？不就是单链表嘛，但是与单链表不同的是，他所存的指针不是next，而是有两个！leftchild和rightchild
链式二叉树最重要的就是他的遍历，分为前序遍历，中序遍历，后序遍历和层序遍历。还有一些求深度，结点个数等。
除去层序遍历，其他大多都可以用递归的方式解决，接下来，我先展示一下前三种遍历当时，后面儿的习题和层序遍历，我就放在下一节啦～
扫一扫
1367
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
